Doherty Andrade
Presidente Prudente, SP

Durante um curso de Aritmética Elementar para professores de 1o. e 2o. graus, um de meus alunos contou o seguinte:

Dado um número inteiro N, se fizermos uma permutação de seus algarismos, obtemos outro inteiro N’.  Se alguém omitir um algarismo, que não seja 0, da diferença  N–N’ e me contar quais são os demais algarismos desta diferença, saberei sempre adivinhar qual foi o algarismo omitido.

Disse o aluno que sabia adivinhar o algarismo omitido, mas não sabia porque o processo que usava sempre “dava certo”.

Vamos desvendar o mistério.

Uma permutação sobre um conjunto A Ø é uma bijeção s de A em  A.

Dado o inteiro  N = anan-1...a1a0, em notação decimal, consideremos uma permutação s sobre o conjunto.

A = {an, na-1, ..., a1, a0}

Representaremos (ai) por a(i). Assim, de uma permutação dos algarismos de N, resulta um inteiro N’ que, em notação decimal, se escreve

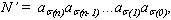
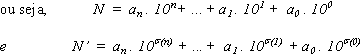
Lema 1. 9 é um divisor de (10n – 1),  para todo natural n.

A demonstração pode ser feita por indução ou observando que 10n – 1 é um número constituído somente de “noves”.

Lema 2. 9  é um divisor de (10 n – 10m), quaisquer que sejam os naturais m e n.

Para provar isto, basta observar que, pelo Lema 1, 9 | (10n – 1) e 9 | (10m – 1), quaisquer que sejam m e n. Portanto 9 divide a diferença, isto é, 9 | (10n – 10m).

Finalmente, temos os seguinte resultado:

Teorema. 9 é um divisor de (N – N’), onde N e N’  são dados como acima.

A prova é trivial. Observe que

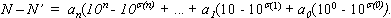
Como 9 | (10n – 10m), segue que 9 | ar(10r - 10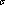(r)) e, portanto, 9 | (N – N’). E o teorema está demonstrado.

Está desvendado, assim, o problema do Nove Misterioso. De fato, se a diferença é sempre divisível por 9, o algarismo omitido é aquele que somado aos demais dá um número divisível por 9.

 

O professor Doherty Andrade é mestre em Matemática pela PUC/RJ, já trabalhou como professor no 2o. grau e é atualmente professor assistente junto ao Departamento de Matemática da Universidade Estadual Paulista em Presidente Prudente. Na UNESP tem realizado, em convênio com a Fundação Rondon, trabalhos na área de Educação. Tem trabalhado também em treinamento de professores de 1o. e 2o. graus através do convênio CENP/UNESP.

 

História verídica

Um pequeno aluno é transferido de escola e é avaliado por uma professora que lhe faz diversas perguntas e lhe propõe o seguinte probleminha: “Se uma banana custa Cz$ 0,30, quanto custam 7 bananas?”

O aluninho diz que não sabe resolver o problema, – que não conhece a operação de multiplicação que a professora, querendo ajudar, lhe sugere fazer – e, finalmente, acaba dizendo: “De banana apenas sei que é um elemento do conjunto cacho”!

(enviado por Lucien Jean F. Thys, Porto Alegre, RS)