Responsáveis
Eduardo Tengan e Élvia Mureb Sallum
Envie suas soluções para
RPM – Problemas
IME/USP – Cidade Universitária
Rua do Matão, 1010, bloco B, sala 105
05508-090 – São Paulo, SP
As soluções dos problemas 356 a 360 serão corrigidas apenas se enviadas até 28 de fevereiro de 2014.
356
Para todo natural n 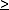 3 prove que existe no plano um conjunto de n pontos tais que 3 prove que existe no plano um conjunto de n pontos tais que
a) a distância entre dois desses pontos é irracional.
b) cada conjunto de três desses pontos determina um triângulo não degenerado de área racional.
357
Mostre que um polinômio do tipo
p(x) = anxn + an-1xn-1 + …. + a3x3 + x2 + x + 1
com coeficientes reais não pode ter todas as raízes reais.
358
Se a, b, c são números reais tais que
a + b + c = 0,
mostre que
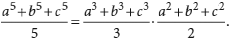
359
Duas casas de um tabuleiro 7 × 7 são pintadas de amarelo e as outras são pintadas de verde. Duas pinturas são ditas equivalentes se uma é obtida a partir da outra por uma rotação do tabuleiro. Quantas pinturas não equivalentes existem?
360
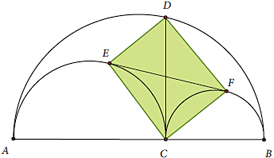
Na figura temos:
 um ponto C qualquer pertencente a um segmento AB, um ponto C qualquer pertencente a um segmento AB,
 semicírculos de diâmetros AB, AC e BC, semicírculos de diâmetros AB, AC e BC,
 o segmento CD perpendicular a AB e o segmento CD perpendicular a AB e
 EF, que é tangente aos dois semicírculos menores. EF, que é tangente aos dois semicírculos menores.
Mostre que ECFD é um retângulo.
PROBLEMINHAS
1
Ao redor de um parque há várias casas. Paulo e Lúcia caminham ao redor do parque, no sentido horário, contando as casas. Partem de lugares diferentes de modo que a 5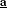 casa de Paulo é a 12 casa de Paulo é a 12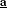 casa de Lúcia e a 5 casa de Lúcia e a 5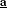 casa de Lúcia é a 30 casa de Lúcia é a 30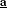 casa de Paulo. Quantas casas existem ao redor do parque? casa de Paulo. Quantas casas existem ao redor do parque?
2
Quatro meninos brincam de “tiro ao alvo”. Cada um atirou três vezes. O alvo tem vários anéis e a figura mostra como ficaram os dardos atirados.

Quem acerta no círculo central ganha 6 pontos, no anel mais próximo do círculo central ganha 5 pontos e assim, sucessivamente, 4, 3, e 2 pontos à medida que os anéis se afastam do centro. Se os quatro meninos empataram, qual foi a contagem para cada jogador?
3
Numa sala de aula há 37 alunos. Desses, 9 têm 3 irmãos e 7 não têm irmãos; os demais têm um ou 2 irmãos. Os irmãos não pertencem a essa sala de aula. Outro dia a professora fez uma festa familiar: todos os alunos compareceram e cada um levou todos os seus irmãos. No total foram 98 crianças. Quantos alunos da sala têm 2 irmãos?
Retirados da Olimpíada Matemática Nandú
SOLUÇÕES DOS PROBLEMAS PRPOSTOS NA RPM 80
346
(a) Mostre que o resto da divisão de 32012 – 1
por 312 – 1 é 38 – 1.
(b) Determine o mdc(32012 – 1; 312 – 1).
SOLUÇÃO
| a) |
O resto da divisão de 32012 – 1 por 312 – 1 é 38 – 1, pois
32012 – 1 = 312×167 + 8 – 1 =
312×167× 38 – 38 + 38 – 1 =
38(312×167 – 1) + (38 – 1) =
38×(312 – 1)×(312×166 + 312×165 + … + 312 + 1) + (38 – 1). |
| |
|
| b) |
Usando o algoritmo de Euclides, tem-se
m.d.c (31012 – 1; 312 – 1) = m.d.c (312 – 1; 38 – 1) e
m.d.c (312 – 1; 38 – 1) = 34 – 1 = 80, pois
312 – 1 = 38 + 4 – 1 = 38 × 34 + 34 – 34 –1
= 34(38 – 1) + 34 – 1 |
(Solução enviada por vários leitores.)
347
Um trapézio é dividido em quatro triângulos por suas diagonais. Sejam A e B as áreas dos triângulos adjacentes aos lados paralelos do trapézio. Encontre a área do trapézio em função de A e B.
SOLUÇÃO
As diagonais dividem o trapézio em quatro triângulos de áreas A, B, C e D conforme indicado na figura.

Tem-se
 |
C = D, pois A + C = A + D (áreas de triângulos com mesma base e mesma altura). |
| |
|
 |
 pois os triângulos de área A e B são semelhantes, com razão de semelhança pois os triângulos de área A e B são semelhantes, com razão de semelhança  . . |
| |
|
 |
 e daí C = ( AB) 1/2 (os triângulos de áreas A e C têm uma base comum com alturas relativas a essa base respectivamente iguais a h e k). |
Logo, a área, A + B + C + D, do trapézio é
A + B + 2 = ( = (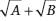 )2. )2.
(Solução enviada por vários leitores.)
348
Por um ponto P exterior a um dado círculo G passam uma secante e uma tangente a G. A secante intercepta G em A e B, e a tangente intercepta G em C, estando A, B e C do mesmo lado do diâmetro que passa por P. Seja Q a projeção de C sobre esse diâmetro. Prove que a reta QC bissecta o ângulo A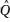 B. B.
SOLUÇÃO
De relações métricas numa circunferência e num triângulo retângulo tem-se
PA.PB = PC2 e PC2 = PQ.PO.
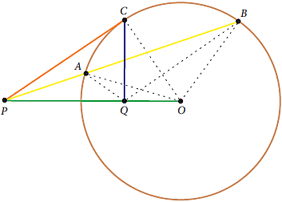
Logo, 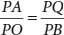 e, como os triângulos APQ e OPB têm em comum o ângulo em P, segue que esses triângulos são semelhantes pelo caso LAL de semelhança de triângulos. e, como os triângulos APQ e OPB têm em comum o ângulo em P, segue que esses triângulos são semelhantes pelo caso LAL de semelhança de triângulos.
Assim, o ângulo Q, do triângulo APQ, e o ângulo B, do triângulo OPB, são congruentes e, portanto, o quadrilátero AQOB é inscritível em uma circunferência, já que tem os ângulos opostos suplementares.
Como o triângulo OAB é isósceles, tem-se  OAB ≡ OAB ≡ PBO ≡ PBO ≡ PQA e, como os ângulos PQA e, como os ângulos  OAB e OAB e  OQB correspondem ao mesmo arco da circunferência circunscrita ao quadrilátero AQOB, segue OQB correspondem ao mesmo arco da circunferência circunscrita ao quadrilátero AQOB, segue  PQA ≡ PQA ≡ OQB. OQB.
Daí,
90o -  PQA ≡ PQA ≡ AQC = 90o - AQC = 90o - OQB = OQB =  BQC. BQC.
(Solução enviada por André Luis Souza de Araújo, RJ.)
349
a) Mostre que cos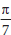 é uma raiz da equação é uma raiz da equação
8x3 – 4x2 – 4x + 1 = 0
b) Encontre todos os números racionais p, q e r tais que
pcos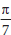 + qcos + qcos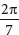 + rcos + rcos = 1. = 1.
SOLUÇÃO
a) Seja a= 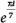 = cos = cos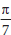 + isen + isen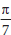 . Pela fórmula de Moivre, . Pela fórmula de Moivre,
a7 = epi = (cos + isen + isen ) = –1 ) = –1
Logo, a7 + 1 = 0 e, como a  0, –1, podemos dividir por a + 1 e a3, obtendo 0, –1, podemos dividir por a + 1 e a3, obtendo
a7 + 1 = 0 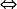 a6 – a5 + a4 – a3 + a2 – a + 1 = 0 a6 – a5 + a4 – a3 + a2 – a + 1 = 0
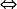 a3 – a2 + a – 1 + a–1 –a–2 + a–3 = 0 a3 – a2 + a – 1 + a–1 –a–2 + a–3 = 0
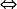 (a3 + a–3) – (a2 + a–2) + (a + a–1) – 1 = 0 (a3 + a–3) – (a2 + a–2) + (a + a–1) – 1 = 0
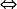 (a + a–1)3 – (a + a–1)2 – 2(a + a–1) + 1 = 0. (a + a–1)3 – (a + a–1)2 – 2(a + a–1) + 1 = 0.
Note que
a + a–1 = 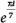 + + 
= (cos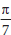 + isen + isen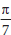 ) + (cos(– ) + (cos(–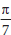 ) + isen(– ) + isen(–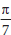 )) = 2cos )) = 2cos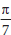 , ,
logo,
(2cos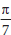 )3 – (2cos )3 – (2cos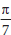 )2 – 2(2cos )2 – 2(2cos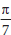 ) + 1 = 0 ) + 1 = 0
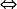 8(cos 8(cos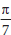 )3 – 4(cos )3 – 4(cos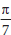 )2 – 4(cos )2 – 4(cos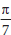 ) + 1 = 0 ) + 1 = 0
b) Como a2 + a–2 = 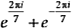 = 2cos = 2cos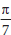 e a3 + a–3 = 2cos e a3 + a–3 = 2cos , temos , temos
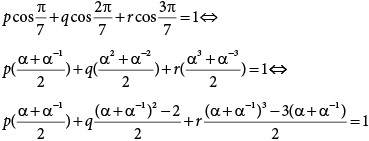
Sendo y = cos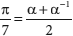 , temos , temos
py + q(2y2 – 1) + r(4y3 – 3y) = 1.
Pelo item anterior, 4y3 = 2y2 + 2y – 1/2, logo temos
py + q(2y2 – 1) + r(2y2 – y –  ) = 1 ) = 1 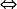
(2r + 2q)y2 + (p – r)y – (q + 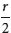 + 1) = 0 + 1) = 0
Vamos mostrar que, se p, q, r  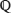 , então a única possibilidade para que isso ocorra é , então a única possibilidade para que isso ocorra é

De fato, observe que 8x3 – 4x2 – 4x + 1 é irredutível sobre 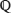 , ou seja, não se fatora como produto de polinômios de grau menor com coeficientes racionais, pois, se isso ocorresse, teria pelo menos um fator de grau 1 e portanto uma raiz racional. Mas, pelo teorema da raiz racional, as raízes racionais de 8x3 – 4x2 – 4x + 1 pertenceriam ao conjunto , ou seja, não se fatora como produto de polinômios de grau menor com coeficientes racionais, pois, se isso ocorresse, teria pelo menos um fator de grau 1 e portanto uma raiz racional. Mas, pelo teorema da raiz racional, as raízes racionais de 8x3 – 4x2 – 4x + 1 pertenceriam ao conjunto  e é fácil ver que nenhum desses valores é raiz de 8x3 – 4x2 – 4x + 1. e é fácil ver que nenhum desses valores é raiz de 8x3 – 4x2 – 4x + 1.
Agora, se existissem a, b, c  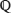 , não todos nulos, tais que ay2 + by + c = 0, então dividindo o polinômio 8x3 – 4x2 – 4x + 1 por ax2 + bx + c, obteríamos um resto r(x) e quociente q(x), tais que , não todos nulos, tais que ay2 + by + c = 0, então dividindo o polinômio 8x3 – 4x2 – 4x + 1 por ax2 + bx + c, obteríamos um resto r(x) e quociente q(x), tais que
8x3 – 4x2 – 4x + 1 = (ax2 + bx + c)q(x) + r(x).
Substituindo x = y =  cos cos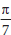 obtemos que r(x) tem y = cos obtemos que r(x) tem y = cos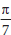 como raiz. Mas r(x) ou é identicamente nulo ou tem grau menor ou igual a 1, ou seja, teríamos que, se r(x) não fosse nulo, então y = cos como raiz. Mas r(x) ou é identicamente nulo ou tem grau menor ou igual a 1, ou seja, teríamos que, se r(x) não fosse nulo, então y = cos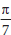 seria racional, o que já vimos ser impossível. seria racional, o que já vimos ser impossível.
E nem podemos ter r(x) nulo, pois, nesse caso, o polinômio 8x3 – 4x2 – 4x + 1 seria o produto de dois polinômios de grau menor com coeficientes racionais. Isso encerra a prova.
350
a) Sejam m, n, k inteiros positivos. Mostre que
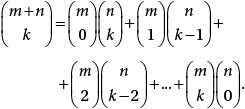
b) Seja p um número primo. Mostre que
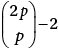
é um múltiplo de p2.
SOLUÇÃO
(a) Suponha que tenhamos um grupo com m + n pessoas, sendo m meninos e n meninas, e queiramos escolher k pessoas desse grupo. O número de maneiras diferentes de fazermos isso é a definição do símbolo  . Mas podemos contar essas diferentes escolhas de outra forma: explicitando o número de meninos escolhidos. Se quisermos escolher 0 menino dentre os m possíveis, teremos de escolher k meninas dentre as n possíveis, e o número de maneiras de fazermos isso é . Mas podemos contar essas diferentes escolhas de outra forma: explicitando o número de meninos escolhidos. Se quisermos escolher 0 menino dentre os m possíveis, teremos de escolher k meninas dentre as n possíveis, e o número de maneiras de fazermos isso é 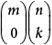 . Se, por outro lado, quisermos escolher 1 menino, teremos de escolher k −1 meninas, e o número de maneiras de fazermos isso é . Se, por outro lado, quisermos escolher 1 menino, teremos de escolher k −1 meninas, e o número de maneiras de fazermos isso é  . E assim por diante, até k meninos e 0 menina. Portanto, a quantidade total de grupos de k pessoas que podemos escolher é dada não só pelo número . E assim por diante, até k meninos e 0 menina. Portanto, a quantidade total de grupos de k pessoas que podemos escolher é dada não só pelo número  , como também pela soma: , como também pela soma:
 . .
Isso prova a igualdade do enunciado.
(b) Primeiramente, observe que, para quaisquer números naturais k < n,
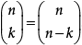
Agora use esse fato e o item a) para escrever:

Portanto,

Para provarmos que esse número é múltiplo de p2, será suficiente provarmos que cada parcela  para j = 1, 2, ..., p − 1, é múltiplo de p. para j = 1, 2, ..., p − 1, é múltiplo de p.
Temos
 , ,
Como p é primo, nenhum fator do denominador j!(p − j)! cancela p no numerador, logo esse binomial é de fato múltiplo de p.
(Solução enviada por vários leitores.)
| Relação
dos leitores que enviaram soluções dos problemas da RPM 80 |
| Almir Del Grossi-SP: 346 |
Luiz Claudio Rego-BA: 346, 347, 348 |
| Amadeu C. de Almeida-RJ: 346, 347, 348, 349, 350 |
Marcelo Ribeiro de Souza-RJ: 346, 347, 350 |
| Amaro J. de Oliveira Filho-PE: 347, 349, 350 |
Marcone Augusto Araújo Borges-SE: 347 |
| Anderson H. C. Barros -MA: 346, 347, 348, 349, 350 |
Milton Dini Maciel-SP: 346, 347, 348, 349, 350 |
| André L. S. de Araújo-RJ: 346, 347, 348, 349, 350 |
Nilton Lapa-SP: 346, 347, 348, 350 |
| Antonio V. Martins -SC: 346, 347, 349, 350 |
Nilton Silveira-MG: 347, 348 |
| Carl H. Schinke-MG: 347 |
Ricardo César da Silva Gomes-CE: 347 |
| Cleunilson B. de Medeiros-DF: 346, 347, 350 |
Ricardo F. Cordeiro-RJ: 346, 347, 348, 340, 350 |
| Dirceu Aparecido Borges-MS: 347 |
Rogério César dos Santos-DF: 346 |
| Dirceu Mora-SP: 347 |
Ronei Lima Badaró-BA: 346 |
| Eduardo Luis Estrada-SP: 346, 347, 350 |
Samuel Francisco-SP: 346, 347, 349, 350 |
| Elias das Neves Freire -RN: 349 |
Sebastião M. dos Santos-MG: 346, 347, 349, 350 |
| Fernando Neres de Oliveira-RN: 346, 347 |
Sérgio Noriaki Sato-SP: 347 |
| Francisco Blasi Jr.-SP: 347 |
Tsunediro Takahashi-SP: 346, 347 |
| Itagiba F. Ferreira Cardia-SP: 347, 349, 350 |
Warles Ribeiro Neto-GO: 347, 348, 349, 350 |
| Jaime Oliveira-SE: 347 |
|
|