Lenimar Nunes de Andrade
UFPB - João Pessoa
Introdução
Questões que envolvem soluções inteiras de equações ocorrem em problemas bem simples, tais como:
| • |
Determinar a idade de uma pessoa no ano de 1999, sabendo-se que essa idade é igual à soma dos algarismos do ano do seu nascimento. (Resposta: 23 anos, nasceu em 1976.) |
| • |
Com R$ 980,00 foram comprados vários livros de três matérias: Matemática, Português e Ciências. Os livros de Matemática custaram R$ 93,00 cada, os de Português R$ 78,00 e os de Ciências, R$ 31,00. Quantos livros de cada uma dessas matérias foram comprados? (Resposta: 3 de Matemática, 7 de Português e 5 de Ciências.)
|
| • |
Determinar o menor inteiro positivo que, ao ser dividido por 8, 11 e 13, fornece os restos 7, 9 e 5, respectivamente. (Resposta: 31.) |
Problemas desses tipos levam a equações de coeficientes inteiros com soluções inteiras – as equações diofantinas, que têm despertado o interesse de matemáticos há séculos. O leitor pode, por exemplo, ler a respeito na RPM 19 – Uma equação diofantina e suas resoluções – ou em livros sobre Teoria dos Números.
Uma equação do primeiro grau com três incógnitas
A título de exemplo, vamos determinar, usando um método apresentado em [1], as soluções inteiras da equação 11x + 8y − 13z = 50 nas variáveis x, y e z. Observe que, para que essa equação tenha soluções inteiras, qualquer divisor comum de 11, 8 e 13 deve ser também um divisor de 50.
| • |
Primeiramente, identificamos o termo da equação com coeficiente de menor valor absoluto; nesse caso, o termo 8 y. Isolamos o valor da variável escrevendo
y = 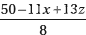 |
| • |
Dividimos os valores absolutos dos coeficientes 50, 11 e 13 por 8 e obtemos os quocientes 6, 1 e 1 e restos 2, 3 e 5, respectivamente. Por isso, a fração que aparece na igualdade anterior pode ser escrita na forma

|
| • |
Separamos a equação anterior em duas, introduzindo uma variável auxiliar t1   : :
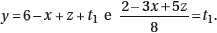
|
| • |
A equação com a variável auxiliar é equivalente a 2 − 3x + 5z = 8t1. Isolamos a variável que tem o menor coeficiente em módulo:
x =  |
| • |
Dividimos 5 e 8 por 3, obtendo quocientes 1 e 2 e restos 2 e 2, respectivamente. Logo, a última equação é equivalente a

|
| • |
Introduzimos a variável auxiliar t2   e separamos a equação anterior em duas:
x = z − 2 t1+ 2 t2 e t2 =  , , que equivale a 1 + z − t1 = 3 t2. |
| • |
Como a equação auxiliar anterior, 1 + z − t1 = 3t2, tem uma variável (x, y ou z) com coeficiente de valor absoluto igual a 1, isolamos o valor dessa variável e fazemos substituições nas equações anteriores para obtermos a solução do problema:
z = t1 + 3t2 − 1,
x = z − 2t1 + 2t2 = (t1 + 3t2 − 1) − 2t1 + 2t2 = −t1 + 5t2 − 1,
y = 6 + z − x + t1 = 6 + (t1 + 3t2 − 1) − (−t1 + 5t2 − 1) + t1 = 3t1 − 2t2 + 6. |
| • |
Obtemos dessa forma a solução geral da equação dada: x = −t1 + 5 t2 − 1, y = 3 t1 − 2 t2 + 6, z = t1 + 3 t2 − 1, com t1, t2   . |
| • |
Atribuindo-se a t1 e t2 valores inteiros, obtemos soluções particulares da equação. Por exemplo, para t1 = 1 e t2 = 0, obtemos a solução: x = −2, y = 9, z = 0. Escolhendo agora t1 = 2 e t2 = −1, obtemos outra solução particular: x = −13, y = 14, z = −2, e assim por diante. |
Soluções positivas
Determinados problemas exigem soluções positivas. Nesses casos, podemos determinar a solução geral da equação segundo o exemplo anterior e depois exigir que cada variável tenha um valor positivo. No caso do exemplo anterior,
 , que equivale a , que equivale a 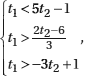 que implica que implica
 , cuja solução é t2 > − , cuja solução é t2 > − e t2 > e t2 >  , ou seja, t2 > , ou seja, t2 >  . .
Logo, podemos ter soluções positivas da equação para os valores inteiros de t2: 1, 2, 3, ... . Substituindo t2 = 1 em um dos sistemas de desigualdades anteriores, obtemos  . Assim, temos para t1: −1, 0, 1, 2 ou 3. . Assim, temos para t1: −1, 0, 1, 2 ou 3.
Escolhendo, por exemplo, t1 = 3 e t2 = 1, substituindo na solução geral da equação, obtemos x = 1, y = 13, z = 5.
Generalizando
Esse método pode ser usado para resolver equações diofantinas de 1 grau com 2, 3, 4, 5, ... variáveis. Começamos isolando a variável que tem o menor coeficiente em módulo, efetuamos algumas divisões e introduzimos uma equação auxiliar construída com coeficientes formados pelos restos das divisões. Repetimos esse procedimento várias vezes, até a equação auxiliar possuir coeficiente de variável de módulo 1. A partir daí, depois de várias substituições, obtemos a solução geral da equação. grau com 2, 3, 4, 5, ... variáveis. Começamos isolando a variável que tem o menor coeficiente em módulo, efetuamos algumas divisões e introduzimos uma equação auxiliar construída com coeficientes formados pelos restos das divisões. Repetimos esse procedimento várias vezes, até a equação auxiliar possuir coeficiente de variável de módulo 1. A partir daí, depois de várias substituições, obtemos a solução geral da equação.
Referência bibliográfica
[1] Menezes, D. L. Abecedário da Álgebra, vol. 1, 1 edição. Departamento de Imprensa Nacional, 1959. edição. Departamento de Imprensa Nacional, 1959.
|