- Uma colega de Avaré-SP, pergunta como achar a área de um quadrilátero irregular, cujos lados medem: 35, 40, 45 e 50 cm.

RPM: O problema colocado não tem solução única e a razão é simples: ao contrário do que acontece com os triângulos, os comprimentos dos lados não determinam um único quadrilátero, nem mesmo sua área. Um exemplo deste fato pode ser observado naqueles “ descansos” para travessas quentes com a forma da figura:

Considerando o contorno desses descansos como lados de um quadrilátero, observamos que a área do quadrilátero varia de uma posição “limite” em que a área é 0 até à área máxima, quando os pontos A, B, C e D formarem um quadrado.

Estudemos as possibilidades que teríamos para os valores de um quadrilátero convexo de lados AB = 7, BC = 8, CD = 9 e DA = 10 (semelhante ao que aparece no seu problema, com razão de semelhança igual a 5), em função do ângulo = BÂD. Esse ângulo a, 0 < < p, determina a diagonal BD que por sua vez nos permite determinar o vértice C. Com efeito, pela lei dos cossenos aplicada ao triângulo ABD, tem-se

BD² = 64 + 49 – 2. 7 . 8 cosa = 113 – 112 cosa =

Para cada valor de , é possível calcular a área do quadrilátero ABCD como soma das áreas dos triângulos ABD e BDC. Usando a fórmula de Heron para o cálculo da área de um triângulo de lados a, b, c:

S() é a área do correspondente quadrilátero:

,

Os cálculos aproximados foram feitos numa calculadora, a lei dos cossenos, e a fórmula de Heron podem ser encontrados em:

- G. Iezzi e outros: Fundamentos da Matemática Elementar, vol. 3 (Trigonometria) e vol. 9 (Geometria Plana).

Observe que, dados quatro números positivos, nem sempre existe um quadrilátero convexo cujos lados tenham estas medidas: a fim de que exista um tal quadrilátero convexo, é necessário e suficiente que o maior deles seja inferior à soma dos outros três.

- Um colega de São Bernardo do Campo – SP, pergunta como encontrar a geratriz de uma dízima periódica simples.

RPM: O conceito de dízima periódica vem explicado na Seção de Conceitos e Controvérsias do nº 2 (RPM, nº 2, pág. 6-8). Este conceito e, conseqüentemente, as justificativas dos cálculos com dízimas periódicas, envolvem a idéia de limite. Como foi dito naquela ocasião, quando se escreve x = 0,222... ou y = 0,27272.... estamos usando uma linguagem simplificada para indicar uma seqüência infinita de frações decimais, cujo limite é o número racional x ou y.

De acordo com as definições dadas naquela ocasião, não é difícil verificar que:

10x = 2,222... = 2 + x

e que 100y = 27,272727.... = 27 + y.

geratriz de uma dízima periódica simples tem para numerador um período e para denominador o número formado por tantos noves quantos forem os algarismos do período”.

Quanto às dízimas periódicas compostas, a geratriz “é uma fração cujo numerador é a parte não periódica seguida de um período, menos a parte não periódica; o denominador tem tantos noves quantos são os algarismos do período, seguinte de tantos zeros quantos são os algarismos da parte não periódica”. Por exemplo:

  ,

A prova é imediata, basta notar (no caso acima) que 999 = 1000 – 1, portanto

(Estamos falando de frações próprias. Se houver parte inteira, acrescentá-la à frente da fração ordinária obtida.)

- Uma colega de São Paulo – SP, pergunta se o seguinte problema tem solução bem determinada: “Dada uma torre vertical DE torna-se o plano horizontal pela sua base D e, neste plano, um segmento AB de 12 m de comprimento cujo ponto médio seja C.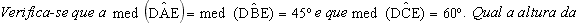
torre?”

RPM: O problema tem solução. Com efeito os triângulos ADE e BDE são retângulos (os ângulos em D são retos) e isósceles, de vez que um dos ângulos agudos mede 45º. Assim, se h = DE é a altura da torre, teremos BD = AD = h. Isto implica também que DC seja a altura do triângulo isósceles ABD e que, portanto

 BD² = CD² + BC² ou h² = CD² + 36 (*)

Por outro lado, no triângulo retângulo CDE (o ângulo D é reto) tem-se , logo

Observe que este enunciado implica que os pontos A, B e D não pertencem a uma mesma reta. De fato, no caso em que D, A e B estivessem alinhados não poderíamos ter pelo Teorema do ângulo externo a um triângulo.

- Um colega de Bauru – SP, envia-nos o seguinte problema: “A figura mostra uma estátua de altura h num pedestal de altura a. O ângulo  é o ângulo segundo o qual a estátua é observada de um ponto Y a uma distância y do pé da estátua. A que distância y o ângulo  será máximo?”

RPM: Façamos alguma considerações preliminares:

1 - Na resolução do problema, usaremos um modelo plano simplificado, em que o observador é representado por um ponto Y de uma semi-reta horizontal PQ e a estátua é representada por um segmento AB, de comprimento h, na perpendicular a PQ por P, num plano . O ponto P será considerado o pé da estátua e o segmento BP, de comprimento a, seu pedestal. O ângulo (Y), segundo o qual a estátua é observada pelo observador Y é o ângulo .

2 - O problema proposto reduz-se, então, às seguintes perguntas:

i)    Deslocando-se o ponto Y na semi-reta PQ, existirá alguma posição X em que o ângulo   seja o maior possível?

ii)    Em caso afirmativo, qual a distância x de X a P?
 

3 - Vale para o cálculo desta distância x comentário análogo àquele sobre o cálculo da altura de uma pirâmide publicado na RPM, nº 4 (pág. 24 e 27) pois, em geral, o ponto P é inacessível.
 

4 - Se a > 0, na posição limite em que Y = P, o ângulo = 0. À medida em que Y se afasta, este ângulo começa a crescer e se Y se afasta demais o ângulo  volta a ser bem pequeno. Intuitivamente, deve haver pelo menos um ponto em que o ângulo  assuma um valor máximo.

Solução para o caso em que a > 0:  a resposta à pergunta i) é: Sim. O ponto X, onde assume seu valor máximo, existe, é único e pode ser obtido do seguinte modo – dentre todas as circunferências (do plano ) pelo pontos A e B, uma única circunferência C é tangente à semi-reta PQ; o ponto X é o ponto de tangência de C com a semi-reta PQ.

Faremos a prova verificando, em primeiro lugar, que a circunferência C existe e é única. Com efeito, uma circunferência por A e B será tangente à reta PQ se, e só se, tiver centro num ponto O eqüidistante, simultaneamente, do ponto A, do ponto B e a reta PQ. Em

Vejamos, agora, que o ponto X de tangência entre C e PQ é a solução da questão i). Isto é, mostremos que se  e se Y X é um outro ponto da semi-reta PQ, tem (Y) < (x). Começamos por observar que, sendo PQ tangente a C em X, o ponto , Y X, é exterior à circunferência C. Então, o segmento AY encontra C num ponto Z (do arco BR, onde AR // PQ). Têm-se, daí:

(ângulo inscritos em C sob o arco AB – v. RPM, nº 6);

e

(teorema do ângulo externo, aplicado ao triângulo YZB);

donde (Y) < (X). Está respondida a pergunta i).

Finalmente, para responder à pergunta ii), calculamos a distância x de X a P usando o fato de que , onde M é o ponto médio do segmento AB e que o triângulo OMB é retângulo. Tem-se, então:

Resposta para o caso que a = 0: não existe o ponto X. De fato, neste caso P = B e o