Manoel F. de Azevedo Filho
Fortaleza – CE.

Sejam A e B dois conjuntos não vazios com m e n elementos, respectivamente. Entende-se  por aplicação de A e B qualquer correspondência f que a cada x A associa um único y B. Se y B está associado a x A, diremos que x é uma  pré-imagem de y e escrevemos f(x) = y. O subconjunto de B dos elementos que admitem pré-imagem é chamado conjunto imagem.

Uma aplicação de A em B é chamada aplicação sobrejetora ou sobrejação se o conjunto imagem é B, ou seja, se cada elemento de B admite pré-imagem. Uma aplicação é dita aplicação injetiva ou injeção se cada elemento do conjunto imagem admite uma única pré-imagem. Prova-se que, quando m = n, numa aplicação é sobrejetiva se, e somente se, é injetiva.

Verifica-se, com certa facilidade, que o número de injeções que podem ser definidas de A em

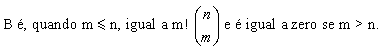
O problema de se estabelecer uma fórmula direta determinando o número de sobrejeções que podem ser definidas de A em B, contudo, não é tão fácil. Esta é uma versão do problema de determinar o número de modos em que se pode distribuir m bolas distintas em n urnas distintas de modo que nenhuma urna fique vazia. Indicaremos este número por (m,n).

É fácil concluir que (m,n) = n! e que (m,n) = 0 se m < n. Nosso objetivo é demonstrar que:

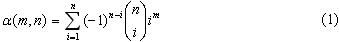
sejam quais forem m e n.

Vale aqui observarmos que deste resultado seguem-se imediatamente os seguintes identidades.

 

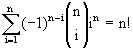
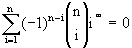
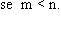
A fim de provar a fórmula (1), mostraremos inicialmente um lema:

 

     Lema

(m,n) = n[ (m-1, n-1) + (m-1, n)], m,n 2.

 

     Demonstração do Lema:

Fixemos um elemento x0 A e consideremos o elemento y0 0, tal que f(x0) = yo. Há duas possibilidades exclusivas:

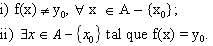
O número de sobrejeções f de A em B tais que f(x0) = y0 satisfazendo i) é igual a (m - 1, n - 1) e satisfazendo ii) é igual a (m - 1,n). Portanto, o numero total satisfazendo f(x0) = y0 é igual a (m -1, n - 1) + (m-1,n). Como existem n possibilidade para y0, segue-se que:

 

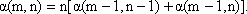
     Demonstração da Fórmula (1)

Faremos a prova por indução sobre m. Isto significa que, para m = 1, devemos mostrar que:

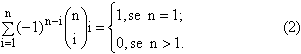
  Ora, se n = 1, temos que:

.

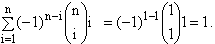Se n = 2, vem

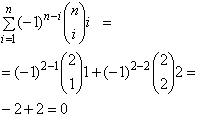
  Suponhamos, agora n > 2: usando a relação de Stifel

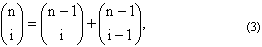
que pode ser verificada diretamente, podemos escrever


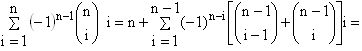
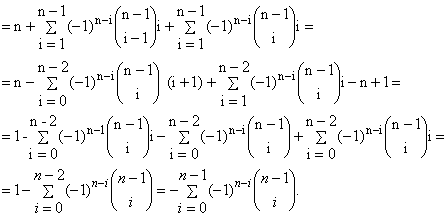
E, pela fórmula do binômio de Newton, temos:

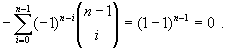
Isto agora a prova de (2) que corresponde ao cálculo de a (m.n) pela expressão em (1) quando m=1 e n qualquer.

Continuando o processo da prova por indução sobre m, suponhamos agora que m 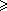2 e que a formula (1) seria válida para m-1 (e n qualquer) e mostremos que ela  também será verdadeira para m (e n qualquer).

Separemos os casos em que  n=1 e n 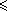2. Com e feito se n=1, temos:

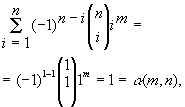
e, portanto, para este caso, a fórmula (1) está provada.

Suponhamos então que n > 1: pelo lema que provamos inicialmente, temos que
(m,n) = n [(m-1,n-1) + (m-1,n)].

Usando a hipótese de indução e mais uma vez a relação de Stifel (3), vem que:

 

______________________
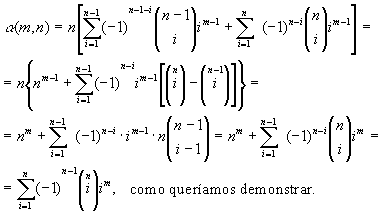
N.R. – O leitor familiarizado com a linguagem de Análise Combinatória pode reconhecer entre os números acima e os números de Stirling da 2ª espécie  S(m,n) a seguinte relação:
 

  (m,n) = n! S (m,n)

(para a definição dos números de Stirling o leitor interessado pode consultar J. Riordan – An Introduction to Combinatorial Analysis, J. Wiley (1958), páginas de 32 a 48, e 91).

 

Eram gratuitos os sapatos?

RPM:

 

1.      Se a historia passasse no instante em que nosso amigo Botelho acabou de vender seus dez selinhos, o que estaria acontecendo é que dez pessoas (os compradores dos selinhos) teriam se cotizado para comprar um par de sapatos para ele.

2.      Na história, nada obriga que cada comprador se limite a adquirir um par de sapatos apenas. Para citar um caso extremo, podemos supor que o primeiro comprador, em vez de vender os 10 selinhos que recebeu da loja, fica com eles e com isso compra mais dez pares de sapatos a 18 mil cruzeiros cada, recebe 100 selinhos., etc, até acabar com o estoque da loja. Depois, revende todos os sapatos ao preço oficial de 200 mil cruzeiros. Em vez de um par de sapatos de graça, ganha muito mais.

3.      Do ponto de vista da loja, o que ela fez corresponde simplesmente a vender cada par de sapatos a 18 mil cruzeiros , exceto o primeiro, vendido por 20 mil. Os selinhos são apenas um truque de marketing. A loja vende por 18 mas, como o preço usual é 20, a diferença é dividida entre alguns felizardos, ou espertos. O exemplo do economista Adão, em que cada habitante da ilha compra apenas um par de sapatos, é o extremo oposto do caso 2 acima. Na prática ocorrem, em geral, situações intermediárias em que algumas pessoas formam estoque para revenda. (Podendo em seguida organizar cartéis para manipular os preços, mas isto já  seria outra história).