Ana Paula Jahn - UNIBAN
Vicenzo Bongiovanni - UNIBAN

Neste artigo vamos provar a impossibilidade das construções com régua e compasso (ver [5]) dos três problemas insolúveis da Antiguidade: a quadratura do círculo, a duplicação do cubo e a trissecção do ângulo. Para isso assumiremos sem provar o teorema de Wantzel, enunciado mais à frente, e abordaremos algumas definições e resultados referentes a números algébricos e transcendentes.

Um número real diz-se algébrico, se ele é raiz de uma equação polinomial de coeficientes racionais. Caso contrário, dizemos que o número é transcedente.
Um número real diz-se algébrico de grau n se ele for raiz de uma equação polinomial de coeficientes racionais de grau n e não for raiz de nenhuma equação polinomial de coeficientes racionais de grau menor que n.

Antes de atacar a impossibilidade dos três problemas, vamos provar que e cos 20o são algébricos de grau 3 sobre Q.

a) é algébrico, pois é raiz da equação x3 - 2 = 0

Se fosse raiz da equação ax + b = 0 com coeficientes racionais, teríamos a + b = 0 , donde = −.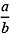
Absurdo, pois o segundo membro é racional. Se fosse raiz da equação do 2º grau ax2 + bx + c = 0 com coeficientes racionais, teríamos a()2 + b + c = 0 (1). Elevando ao quadrado os membros da igualdade a()2 + b = −c , obtém-se 2a2 + 4ab + b2 = c2 (2). Multiplicando (1) por b2 e (2) por −a e adicionando membro a membro, chega-se a: , um absurdo já que é irracional (observe que b3 − 2a3 ≠ 0, pois caso contrário teríamos b/a = , absurdo, pois a e b são racionais). Logo, é algébrico de grau 3 sobre Q.

b) cos 20o é algébrico, pois é raiz da equação 8x3− 6x − 1 = 0. De fato, 8(cos 20o)3 − 6(cos 20o) − 1 = 2[4(cos 20o)3 − 3(cos 20o)] − 1 = 2cos 60o − 1 = 2(1/2) − 1 = 0. Se cos 20o fosse raiz da equação do 1 grau ax + b = 0 com coeficientes racionais, teríamos cos 20o = −b/a. Absurdo, pois cos 20o não é racional (basta aplicar o teorema das raízes racionais(*) na equação 8x3 − 6x − 1 = 0). Se cos 20o fosse raiz de uma equação do 2 grau ax2 + bx + c = 0 com coeficientes racionais, dividindo o polinômio 8x3 − 6x − 1 pelo polinômio ax2 + bx + c teríamos o quociente mx + n e o resto px + q com coeficientes racionais. Conseqüentemente, 8x3 − 6x − 1 = (ax2 + bx + c)(mx + n) + (px + q). Fazendo x = cos 20o teremos pcos 20o + q = 0. Donde p = q = 0, pois cos 20o, não é racional. Logo, o resto da divisão é nulo e 8x3 − 6x − 1 = (ax2 + bx + c)(mx + n). Essa igualdade mostra que o racional −n/m é raiz da equação 8x3 − 6x − 1 = 0. Mas o teorema das raízes racionais garante que essa equação não admite raízes racionais. Logo, cos 20o não é raiz de uma equação polinomial de grau 2 de coeficientes racionais, implicando cos 20o algébrico de grau 3.

Em 1844, Liouville demonstrou que existe um número que não é raiz de uma equação polinomial de coeficientes racionais, ou seja, que existe um número transcendente sobre Q. Esse número é chamado de número de Liouville. Seu valor é 10−1! + 10−2! + 10−3! + ... = 0,1 + 0,01 + 0,000001 +... . Em 1882 Lindemann provou que π é transcendente.

Antes de provar a impossibilidade dos três problemas, vamos apresentar um último resultado. A partir de um segmento de comprimento 1 e de um segmento de comprimento a, podese construir com uma régua não graduada e um compasso um segmento de comprimento a2. De a2 = x, temos . O teorema de Tales garante a construção do segmento de comprimento x.

E quais outros segmentos podem ser construídos com régua não graduada e compasso? Em 1837, Wantzel prova o teorema: "se um número é construtível (pode ser construído com régua não graduada e compasso), então ele é algébrico de grau n sobre Q com n igual a uma potência de 2". A recíproca do teorema de Wantzel não é verdadeira. Existem polinômios de grau potência de 2 com raízes reais não construtíveis. Exemplo: x4 − px + 1 = 0 com p primo maior que 2. A contrapositiva do teorema de Wantzel pode ser enunciada da seguinte maneira "se um número não é algébrico ou algébrico com grau diferente de uma potência de 2, então ele não pode ser construído com régua não graduada e compasso".

O problema da duplicação do cubo consiste em construir a aresta de um cubo de volume igual ao dobro do volume de um cubo de aresta dada, utilizando apenas uma régua não graduada e um compasso. O problema pode ser colocado nos seguintes termos: dado um segmento de medida a, construir um segmento de medida x tal que x3 = 2a3. Vamos supor que seja posssível construir com régua não graduada e compasso um segmento com medida x tal que x3 = 2a3. Em particular, fazendo a = 1 teríamos a equação que x3 − 2 = 0 cuja raiz é , que mostramos ser algébrico de grau 3 (que não é potência de 2) e, portanto, o segmento de medida não pode ser construído. Logo, o problema da duplicação do cubo é impossível.

O problema da quadratura do círculo consiste em construir um quadrado de área igual à de um círculo dado usando apenas uma régua não graduada e um compasso. Isso equivale a construir o lado de um quadrado de medida x, com x2 = πr2. Em particular, fazendo r = 1, teríamos x2 = π. Supondo possível construir um segmento de medida x = , seria possível construir o segmento de medida π. Mas π é transcendente. Logo, é impossível quadrar o círculo.

O problema da trissecção de um ângulo consiste em dividir em três partes iguais um ângulo qualquer utilizando apenas uma régua não graduada e um 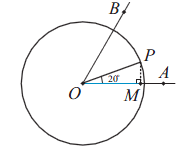compasso. Vamos supor que a construção seja possível e tomemos, em particular, o ângulo AOB, de medida 60o, numa circunferência de centro O e raio 1 conforme figura. Se pudéssemos construir o ponto P, traçaríamos a bissetriz do ângulo BOP, que mede 40o, e teríamos a solução do problema. Para construir P, seria necessário construir o segmento OM. Tendo construído o segmento OM, bastaria traçar a perpendicular e obter P. Reciprocamente, construído P, obtém-se M. A questão é saber se é possível construir o segmento de medida OM. A resposta é negativa, pois OM = cos20o, que mostramos ser algébrico de grau 3, logo, não construtível.

Bibliografia e referências bibliográficas

[1] BASTOS, G. Números reais não construtíveis de grau 4. Revista Andrade, vol. 4, 2003.
[2] BOYER, C. B. História da Matemática. São Paulo: Edgard Blücher, 1996.
[3] COURANT, R. e ROBBINS, H. O que é a Matemática? Ciência Moderna, Rio de Janeiro, 2000.
[4] NIVEN, I. Números racionais e irracionais. SBM, Rio de Janeiro, 1984.
[5] WAGNER, E. e CARNEIRO, J. P. Q. Construções geométricas. SBM, Rio de Janeiro, 2007.