 |
|
|
||
 |
||||
|
|
|
|
||
|
|
||||
|
Divaldo Portilho F. Junior
Este artigo trata de uma interessante relação entre um problema de Física e um assunto abordado com pouca freqüência em textos para ensino médio, a teoria das frações contínuas. A solução do problema envolve, de forma intuitiva, o uso de aproximações sucessivas por métodos recursivos. O problema é o seguinte: Determine a resistência equivalente (sobre este conceito da Física, ver Apêndice) no circuito ilustrado na figura abaixo, no qual temos uma associação de infinitos resistores de resistência igual a R.
Para uma primeira abordagem do problema, vamos calcular a resistência equivalente para os primeiros cinco passos do processo, no intuito de nos orientarmos rumo a uma generalização.
A experiência com este problema em sala de aula conduziu à observação de que aparentemente os valores convergem, ou seja, as variações entre as resistências equivalentes em passos sucessivos vão rapidamente diminuindo e se tornando menores do que qualquer valor positivo, na medida em que se acrescentam novos conjuntos de resistências ao processo. Seguindo o caminho esboçado pelos cálculos iniciais, conseguimos generalizar o caso acima por meio de uma recursão que entusiasmou tanto os alunos quanto os professores de Física. A respeito da teoria sobre frações contínuas, o leitor pode encontrar valiosas informações nas referências [2] e [3]. Aqui, usaremos apenas alguns fatos simples dessa teoria, para chegar à solução do problema proposto. Acompanhe os passos, em que o circuito vai sendo montado gradativamente, onde Rn denota a resistência equivalente do circuito apresentado no n-ésimo passo: 1 2
3
4
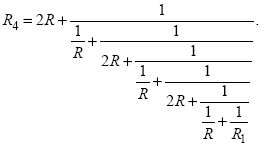
Quando o problema fala da “associação de infinitos resistores”, nosso interesse se volta para o “limite” desse processo. Vamos chamar de x o valor da resistência equivalente para n tendendo ao infinito, ou seja,
Os “pontinhos” indicam que se trata de um processo infinito. A experiência que fizemos com os cinco primeiros casos sugere que esse limite exista e seja algo próximo de 2,732. Vamos ver por quê. Admitindo a existência desse limite (que pode ser demonstrada), podemos escrever:
Como o processo é infinito, o x que aparece no retângulo da figura é o mesmo x inicial. Isso nos dá a equação:
x2 − 2Rx − 2R2 = 0, que tem como solução positiva: x = R( 1 + Naturalmente, como
Resistência Equivalente em Associação de Resistores Resistências ligadas em série Quando duas resistências, R1 e R2, são ligadas em série, como mostrado na figura abaixo, a resistência equivalente desse circuito é dada por Req = R1 + R2.
De fato: a resistência equivalente é definida como a resistência R que, se substituída a R1 e R2, produz a mesma corrente entre os pontos A e B, que estão sob a diferença de potencial VAB. Tomando um ponto C entre R1 e R2, tem-se:
. Resistências ligadas em paralelo Ao ligar duas resistências, R1 e R2, como na figura abaixo, a resistência equivalente desse circuito é dada por
De fato, a corrente i que sai de A e chega em B se divide em duas parcelas: i1, que atravessa a resistência R1, e i2, que atravessa a resistência R2. Temos, então:
Referências bibliográficas [1] CARLOS, KAZUHITO e FUKE. Os alicerces da Física, vol. 3. Editora Saraiva: 1993.
|
Passo
que podemos representar por:
Essa equação pode ser escrita como: 
), que é a resistência equivalente do circuito apresentado.
3, p. 44-55, 1998.