Carlos A. Gomes
João Pessoa/UFPB

As pessoas criaram um mito sobre as sextas-feiras 13, dizendo que essas datas são propícias para ocorrer coisas macabras, horríveis... Parece que nas últimas décadas esse mito foi bastante reforçado e divulgado pela série de filmes Sexta-feira 13 que o cinema exibiu. Mas não são apenas coisas ruins que estão ligadas à sexta-feira 13, muito pelo contrário; temos um belo problema de Matemática: todo ano há pelo menos uma sexta-feira 13.

Para verificarmos o prometido, vamos inicialmente enumerar os dias 13 de um determinado ano. Para isso imaginemos um ano de 365 dias (se o ano tiver 366 dias, o mesmo método funciona!). Lembre que, num ano de 365 dias, os meses de janeiro, março, maio, julho, agosto, outubro e dezembro têm 31 dias, enquanto abril, junho, setembro e novembro têm 30 dias e fevereiro tem 28 dias. Assim, temos que:

 

	1o de janeiro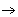dia 1			13 de junho 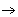dia 164
	2 de janeiro 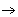dia 2			. . .
	3 de janeiro 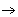dia 3			13 de julho 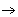dia 194
	. . .			. . .
	13 de janeiro 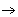dia 13			13 de agosto 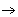dia 225
	. . .			. . .
	13 de fevereiro 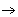dia 44			13 de setembro 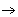dia 256
	. . .			. . .
	13 de março 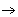dia 72			13 de outubro 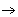dia 286
	. . .			. . .
	13 de abril 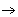dia 103			13 de novembro 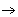dia 317
	. . .			. . .
	13 de maio 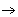dia 133			13 de dezembro 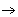dia 347
	. . .

Assim, temos que os dias 13 de um determinado ano de 365 dias são 13, 44, 72, 103, 133, 164, 194, 225, 256, 286, 317 e 347, que, quando divididos por 7 (uma semana tem sete dias), deixam restos 6, 2, 2, 5, 0, 3, 5, 1, 4, 6, 2 e 4, respectivamente. Perceba que todos os restos possíveis de uma divisão por 7 apareceram, isto é, 0, 1, 2, 3, 4, 5 e 6. Assim, perceba que:

se a primeira sexta-feira do ano for dia x (x é no máximo 7), as sextas-feiras seguintes serão os dias x + 7, x + 14, x + 21, ... Se, por exemplo, x for 7, então todas as sextas-feiras do ano cairão nos dias 7, 14, 21, 28, 35, 42, ... do referido ano. Como entre os dias 13 há um que é múltiplo de 7 (o dia 133), segue que esse dia será uma sexta-feira 13 (isso ocorreu em 2005; veja que 13 de maio de 2005 foi uma sexta-feira 13). Seguindo o mesmo raciocínio, se a primeira sexta-feira do ano fosse dia 6 de janeiro, então as sextas-feiras seriam os dias 6, 13, 20, 27, 34, 41, ... Como entre os dias 13 há um cujo resto da divisão por 7 é 6 (o dia 13), segue que, nesse ano, 13 de janeiro seria uma sexta-feira 13.

Esse raciocínio mostra que em qualquer ano existe pelo menos uma sexta-feira 13. Perceba que pode haver mais de uma sexta-feira 13. Se, por exemplo, o dia 2 de janeiro for uma sexta-feira, então as demais sextas-feiras desse ano serão os dias 2, 9, 16, 23, 30, 37,44, ..., ou seja, os dias que deixam resto 2 quando divididos por 7.

Assim, em um ano de 365 dias em que 2 de janeiro é uma sexta-feira, os dias 44, 72 e 317 (que divididos por 7 deixam resto 2) seriam sextas-feiras 13. Noutras palavras, 13 de fevereiro, 13 de março e 13 de novembro seriam sextas-feiras 13 (que ano azarado, hein??? Prepare-se, 2009 será assim!).