|
Alciléa
Augusto
Rio de Janeiro,
RJ
Correspondência:
RPM – Cartas do leitor
Caixa Postal 66281
05311-970 São Paulo, SP
|
 |
|
Um fractal
de dimensão inteira |
Escreve-nos a colega Fátima Maria H. S. Pereira
da Silva, de Ribeirão Preto, SP, comentando a frase do artigo
Fractais no ensino médio (RPM 57, p. 1), de autoria
de Élvia M. Sallum: Seu nome se deve ao fato de que a dimensão
de um fractal não é um número inteiro. Ela
lembra que essa dimensão pode ser também um número
inteiro e apresenta um exemplo de fractal no espaço, cuja dimensão
é o número inteiro 2. Trata-se do Tetraedro de Sierpinski.
Em sua carta, ela escreve:
Sua construção se inicia com um tetraedro,
ou seja, uma pirâmide de base triangular, de volume igual a V.
Usando a mesma terminologia descrita pela colega Élvia, podemos
tomar uma redução do fractal de 1/4 e reunindo,
adequadamente, 16 cópias dessa redução,
obtemos o fractal original. Assim, podemos afirmar que a massa M(1/4)
dessa redução corresponde a 1/16
da massa M(V) da figura que originou o fractal,
isto é,
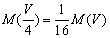 e e 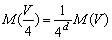 . Daí: . Daí: 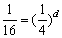 . Portanto, d = 2. O que é equivalente a dizer
que d = log 16/ log 4 = 2. . Portanto, d = 2. O que é equivalente a dizer
que d = log 16/ log 4 = 2.
RPM
Agradecemos a pertinente observação da
colega, que envia as fotos a seguir, dentre outras, que se encontram
no endereço:
http://www.public.asu.edu/~starlite/sierpinskitetrahedron.html,
|
Um fractal
de dimensão inteira |
Escreve-nos o colega Adalberto A. Dornelles Filho,
de Caxias do Sul, RS, sobre o item Você sabia? da seção
O leitor pergunta (RPM 57, p. 58). Naquela ocasião,
a Revista respondeu a uma questão proposta pelo colega Gilder
da Silva Mesquita (RPM 48, p. 49) sobre uma tabela de 6 colunas
e 6 linhas preenchidas com os números de 1 a 36. O missivista
observa que a situação se repete ainda que se considere
uma matriz quadrada de ordem n qualquer:
|
1 + 0.n |
2 + 0.n |
... |
(n - 1) + 0.n |
n + 0.n |
|
1 + 1.n |
2 + 1.n |
... |
(n - 1) + 1.n |
n + 1.n |
|
... |
... |
... |
... |
... |
|
1 + (n - 2)n |
2 + (n - 2)n |
... |
(n - 1) + ( n - 2)n |
n + ( n - 2)n |
|
1 + (n - 1)n |
2 + (n - 1)n |
... |
(n - 1) + ( n - 1)n |
n + ( n - 1)n |
E calcula o que ele chama de M(n),
o "número mágico" para um tal quadro, resultado
da soma de n quaisquer dos números, escolhidos um e apenas
um de cada linha e de cada coluna. Por exemplo, somando-se os elementos
da diagonal principal:


RPM
Curiosidades desse tipo servem ao professor das séries
iniciais para montar questões em que os alunos façam muitas
operações de modo interessante, movidos pela curiosidade.
Nas séries mais avançadas, elas propiciam oportunidades
para o estudante procurar provas ou contra-exemplos ou, mesmo, descubrir
outras situações em que se possa prever a soma.
O Comitê Editorial tem muito interesse em que
a RPM ajude o professor em suas atividades didáticas.
Buscando melhor cumprir esse objetivo, a Seção de Cartas
solicita ao leitor que está em sala de aula que escreva,
sempre que possível, destacando os artigos que gosta de ler,
aqueles que servem para aumentar sua cultura matemática, aqueles
que lhe esclareceram alguma dúvida, aqueles que lhe deram alguma
idéia para levar a seus alunos. Tais informações
vão ajudar o Comitê na sua tarefa de produzir uma revista
mais útil e agradável ao professor.
"Eu
sou o Papa!" |
O leitor Maurílio Machi escreveu para a RPM:
"Lendo a RPM 58, p. 61, deparei com o texto Eu sou o Papa!.
A referência quanto ao autor desse paradoxo (?) explicita
o matemático G. H. Hardy (1877-1947). Uma outra referência:
o livro de Dimas Monteiro de Barros, Enigmas, desafios, paradoxos
e outros divertimentos lógicos e matemáticos,
Araçatuba, Nova Conquista Editora, 2003, p. 27, descreve
o mesmo texto, sendo de autoria de Bertrand Russel (1872-1970).
Também pelos conhecimentos que conquistamos durante a
vida, sempre tive como autor Bertrand Russel. E agora?"
A RPM responde
Quem foi o autor da "tirada":
Se 2+2= 5, então eu sou o Papa?
Inicialmente, não se trata de um paradoxo,
e sim de um raciocínio perfeito, apenas colocado em termos
humorísticos.
O tema pertence ao folclore matemático.
Se você for procurar em diversas fontes (por exemplo,
na Internet), vai encontrar o tema em versões
diferentes, e atribuídas, ora a Russell, ora a Whitehead,
ora a Hardy. Para ver como ninguém tem certeza da origem
exata da história, pode-se consultar o site "Canonical
List of Mathematical Jokes":
http://users.characterlink.net/The-Cookie-Jar/math_jokes_03.html,
onde se lê:
"Não tenho certeza se a história
que segue é verdadeira: O grande lógico Bertrand
Russell (ou terá sido A.N. Whitehead?) declarou certa
vez que poderia demonstrar qualquer coisa, uma vez aceito que
1+1=1. Então, um dia um gaiato o desafiou: "Muito
bem. Demonstre que você é o Papa". Ele pensou
por um instante e enunciou: "Eu sou um. O Papa é
um. Então, o Papa e eu somos um".
O que segue é de responsabilidade de
Merritt
(merritt@Gendev.slc.paramax.com):
"Eu acredito que esta história
foi, originalmente, o produto de uma conversa na Alta Mesa do
Trinity [College, em Cambridge, Reino Unido], registrada em
Scientific Inference, de Sir Harold Jeffreys, em uma
nota do capítulo 1 [...]. Segundo Jeffreys, foi McTaggart
que lançou no ar o desafio:
"Se 2 + 2 = 5, como se pode provar que
eu sou o Papa?". Supostamente, Hardy respondeu: "If
2 + 2 = 5, 4 = 5; subtraindo 3, então 1 = 2; mas McTaggart
e o Papa são dois; então McTaggart e o Papa são
um." [...] Como McTaggart, Hardy, Whitehead, e Russell
[...] eram todos fellows de Trinity, e Jeffreys (exato
contemporâneo deles) era um fellow do St. Johns
[College], eu suspeito que, se a história de Jeffreys
for verdadeira, é muito improvável que Whitehead
ou Russell tenham alguma coisa a ver com ela. O que há
de extraordinário para mim nesta história é
o fato de que Hardy tenha concebido de improviso este argumento,
e ele nem era um lógico. Esta é provavelmente
a razão pela qual ocorreu a alguns atribuir a história
a um dos dois famosos lógicos de Trinity."
Esclarecimentos: McTaggart era um filósofo
hegeliano, muito amigo de Bertrand Russell. Russell (1872-1970)
foi uma das maiores inteligências do século XX:
filósofo, matemático, prêmio Nobel de Literatura
(!) e ativista político.
|
|
|
Respostas dos
...probleminhas
1. 2.
2. 40 km.
3. 25 anos.
|
|