| Cláudio
Possani
IME - USP
O objetivo desta nota é divulgar junto aos leitores
da RPM uma demonstração da irracionalidade de 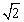 ,
extremamente elegante e fundada em argumentos geométricos. Aparentemente,
o argumento central já fora utilizado pelos gregos na demonstração
da incomensurabilidade do lado e da diagonal de um quadrado. Para maiores
detalhes, ver o artigo Grandezas incomensuráveis e números
irracionais, publicado na RPM 5. ,
extremamente elegante e fundada em argumentos geométricos. Aparentemente,
o argumento central já fora utilizado pelos gregos na demonstração
da incomensurabilidade do lado e da diagonal de um quadrado. Para maiores
detalhes, ver o artigo Grandezas incomensuráveis e números
irracionais, publicado na RPM 5.
Começamos observando que, da igualdade 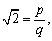 obtemos p2 = 2q2 = q2
+ q2, que é a relação do Teorema
de Pitágoras. obtemos p2 = 2q2 = q2
+ q2, que é a relação do Teorema
de Pitágoras.
Assuma, por absurdo, que 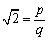 , com p e q números inteiros positivos
e primos entre si. Assim, existirá um triângulo retângulo
isósceles de lados inteiros p (hipotenusa) e q
(catetos). Observe que quaisquer dois triângulos retângulos
isósceles são semelhantes e, como p e q não
possuem fator comum, esse triângulo de lados p, q
e q é o menor triângulo retângulo isósceles
de lados inteiros. , com p e q números inteiros positivos
e primos entre si. Assim, existirá um triângulo retângulo
isósceles de lados inteiros p (hipotenusa) e q
(catetos). Observe que quaisquer dois triângulos retângulos
isósceles são semelhantes e, como p e q não
possuem fator comum, esse triângulo de lados p, q
e q é o menor triângulo retângulo isósceles
de lados inteiros.
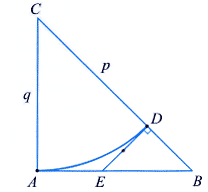 Na
figura, Na
figura, 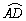 é um arco de circunferência de raio q e
centro C, com D é um arco de circunferência de raio q e
centro C, com D  CB. Toma-se E em AB de modo que
CB. Toma-se E em AB de modo que 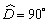 . Daí segue que DE é tangente ao arco de
circunferência mencionada e, também, que EA = ED,
já que são segmentos tangentes à circunferência
traçados a partir de um ponto externo. . Daí segue que DE é tangente ao arco de
circunferência mencionada e, também, que EA = ED,
já que são segmentos tangentes à circunferência
traçados a partir de um ponto externo.
Como 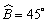 , segue que o triângulo EDB é isósceles
e retângulo. , segue que o triângulo EDB é isósceles
e retângulo.
ED = DB = p - q, que é
inteiro. Também EB é inteiro, pois EB = p
- AE = q - ED = q - (p -q) =
2q - p.
Assim, o triângulo DEB é retângulo
isósceles e possui lados inteiros menores do que p e q.
Isso é um absurdo que seguiu da suposição 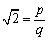 , com p e q inteiros primos entre si. A conclusão
é que , com p e q inteiros primos entre si. A conclusão
é que 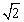 é irracional. Bonito, não é? é irracional. Bonito, não é?
|
Selos
Matemáticos |
 |
Selo em homenagem a Abel (Noruega 1929)
comemorando o centenário de sua morte. |
|
| |
Selos comemorativos do Ano
Mundial da Matemática (2000) |
|
|
| Selo da França de 1937 em Comemoração
do 3o centenário da publicação
do Discurso do Método, de Descartes. |
 |
|
|
Fonte: Internet.
|