 |
|
|
|||
 |
|||||
|
|
|
|
|||
|
|
|||||
| José
Luiz Pastore Mello
A utilização do geoplano como ferramenta didática para o ensino de tópicos da geometria é bem conhecida, embora haja outras possibilidades de uso desse dispositivo didático. Propõe-se neste artigo a apresentação do geoplano como recurso visual para o estudo dos números racionais e de algumas de suas propriedades. A atividade pode ser realizada, com um geoplano construído com madeira, cortiça ou isopor, em que os pontos da malha são marcados com pregos, percevejos ou alfinetes.
Números racionais são aqueles que podem
ser escritos na forma de fração
 , com p e q inteiros, e q  0. Assim,
podemos associar a cada número racional um par ordenado de inteiros
(p, q), o que permitirá a visualização
desse número em um geoplano ordenado (geoplano com  marcações
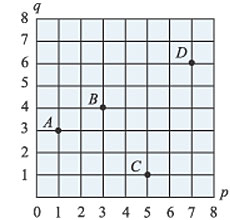
numéricas) como o da figura. Sem perda de generalidade,simplificaremos nossa análise estudando apenas as frações com numeradores e deno-minadores positivos em um geoplano 8´8, lembrando que o estudo torna-se mais interessante em geoplanos maiores. Por exemplo, na figura, os pontos A, B,
C e D representam, respectivamente, os números racionais
Utilizando elástico, linha ou barbante, podemos, como exercício, começar a praticar o uso do geoplano ordenado fazendo as seguintes marcações: 1) todas as frações diferentes de zero com denominador 5; 2) todos os números naturais diferentes de zero; 3) todas as frações equivalentes a 1/2. As respostas estão ilustradas na figura abaixo.
Complementando o exercício, podemos observar que:
O geoplano ordenado também permite determinar
um procedimento para fazer adição de 1) marcamos o conjunto de frações equivalentes a 1/2; 2) marcamos o conjunto de frações equivalentes a 2/3; 3) procuramos frações dos conjuntos marcados que estejam alinhadas horizontalmente e, nessa mesma linha de alinhamento, encontramos o resultado da operação adicionando os numeradores das frações de denominador comum.
Uma outra tarefa simples que pode ser feita com o uso do geoplano é a ordenação de um subconjunto de números racionais. Observe, no exemplo anterior, que podemos concluir que
Imaginemos agora uma situação em que o geoplano representa uma floresta, sendo cada ponto a representação de uma árvore muito fina. Se estivéssemos localizados na origem, e olhando na direção da floresta, quais árvores seriam visíveis? Uma árvore correspondente à fração
Explorando essa idéia para outras frações,
podemos dizer que um ponto (p, q) do geoplano é visível
da origem se e somente se p e q são números
primos entre si, o que implica dizer que as árvores visíveis
são aquelas representadas por frações irredutíveis
Sabemos que o conjunto dos racionais é enumerável (ver RPM 4, p. 4-8), o que significa dizer que podemos estabelecer uma correspondência biunívoca entre o conjunto dos racionais e o dos números naturais (lembramos mais uma vez que, para efeito de simplificação, estamos trabalhando apenas com os racionais positivos). Uma vez que a representação das árvores visíveis a partir da origem indica todas as frações irredutíveis que compõem o conjunto dos racionais, podemos utilizá-la para colocar os racionais em fila, o que possibilitará estabelecer a bijeção entre Q e N:
Nesta representação, torna-se intuitiva a seguinte propriedade dos números racionais: Se r, s são racionais com r < s, então existe um outro racional t tal que r < t < s. Em palavras, entre dois racionais sempre existe um terceiro racional. No geoplano, essa propriedade se verifica pelo fato de haver sempre uma reta ligando a origem a um ponto de coordenadas inteiras situado "entre" as retas correspondentes aos dois números racionais dados. A figura a seguir mostra, por exemplo, a fração
Em um geoplano infinito, as árvores visíveis da floresta indicariam todos os números racionais. Imaginando um observador localizado na origem do geoplano, e com visão em linha reta de alcance infinito, poderíamos nos perguntar: será que, para qualquer direção que aponte a linha de visão do observador, ele irá enxergar uma árvore? Sabemos que isso não é verdade porque existem números que não podem ser escritos como quociente de inteiros: os números irracionais. Por exemplo, se a linha de visão do observador
for representada por uma reta com declividade As retas próximas a
Algumas dessas aproximações cometem erro
por excesso, como
Todas as frações Observe na figura que as retas que passam por
Referências bibliográficas [1] GARDNER, Martin. The Lattice of
Integers (in Sixty book of mathematical games from Scientific American.
San Francisco, W. H. Freeman and Company, 1971).
|
as frações de mesmo denominador necessariamente estão
alinhadas horizontalmente;
frações.
Por exemplo, para fazer 
, os passos são:
pela comparação das frações equivalentes
. Outra maneira de verificar isso é ver que a inclinação
da reta pela origem que corresponde à fração 
é maior que a inclinação da reta pela origem
que corresponde à fração 
. Ou seja, quanto maior a inclinação, menor é
a fração e, de fato, a inclinação da reta
é o inverso da fração correspondente.
não seria visível por ter à sua frente
as árvores correspondentes a 
. Nessa linha de visada, a única árvore visível
seria aquela correspondente à fração 
.
, como mostra a figura a seguir.
Frações
irredutíveis (árvores visíveis) 
caminho
de ordenação de todas as frações irredutíveis
a partir de 1/1. 
, que denotaremos 
, essa reta nunca interceptará uma árvore da floresta.
e outras por falta, como 
cujos inversos 
cometem erros por excesso estão localizadas à esquerda
da reta de declividade 
são boas aproximações de 
e 
(
). Num geoplano 20´20 poderemos obter aproximações
melhores, como 17/12, em que o erro (por excesso) se dá apenas
na terceira casa decimal.