230. Dado o sistema

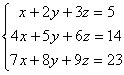
determine quais condições devem ser satisfeitas por a, b e c para que ax + by + cz tenha o mesmo valor para todas as soluções (x, y, z) do sistema.

231. Se a é um número real tal que cos = 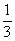, mostre que e são incomensuráveis, isto é, não existem inteiros p e q tais que p = q.

232. Se C₁, C₂ e C₃ são três circunferências concêntricas distintas, mostre que existem 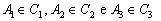tais que o triângulo A₁A₂A₃ é equilátero e calcule o lado do triângulo em função dos raios das circunferências. Discuta a existência de soluções não congruentes. (Enviado por Gilberto G. Garbi, PR)

233. Dado um octaedro regular de arestas com medida a, prove que colando tetraedros regulares, de arestas também com medida a, em duas faces opostas (paralelas) do octaedro obtém-se um poliedro que é um paralelepípedo. Observe que segue do resultado que o espaço pode ser preenchido com tetraedros e octaedros regulares.

1. O governo do Estado de São Paulo, alterou a cobrança da contribuição previdenciária de seus funcionários. A contribuição que era de 6% sobre o salário total, passou a ser de 11% sobre a parte que exceder R$ 1200,00. Um funcionário fez os cálculos e descobriu que continuaria contribuindo com a mesma quantia. Qual é seu salário? (Resp. R$ 2640,00)

2. Existe algum número da forma qqpp que seja quadrado perfeito, onde p e q são algarismos e q 0? (Resp.: 7744)
(XXII Olimpíadas Portuguesas de Matemática)

3. O João e a Maria decidiram partilhar um tablete de chocolate que estava dividida em quadradinhos. O João é muito guloso e, na ausência da Maria, comeu todos os quadradinhos da borda do tablete, na esperança de que a Maria não desse pela diferença. A Maria não se deixou enganar e comeu todos os quadradinhos restantes. Sabendo que ambos comeram o mesmo número de quadradinhso, quantos quadradinhos podem ter os lados deste tipo de tablete? (Resp.: 5 x 12 ou 6 x 8)
(XXII Olimpíadas Portuguesas de Matemática)

222. Para n 1, determine, em função de n, de quantas maneiras podemos escolher 3 números distintos no conjunto {1, 2, ..., 3n} de modo que a soma dos números escolhidos seja divisível por 3.

Solução
Vamos subdividir o conjunto dado em 3 subconjuntos disjuntos: A₀, A₁ e A₂, sendo esses subconjuntos formados pelos números que deixam, respectivamente, resto 0, 1 e 2 quando divididos por 3.
Teremos então:

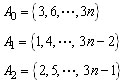
É fácil mostrar que se 3 números distintos forem escolhidos em um desses três subconjuntos, a soma deles será sempre divisível por 3. Assim, por exemplo, se escolhermos 3 números em A₂, teremos:

3u + 2 + 3v + 2 + 3w + 2 = 3(u + v + w + 2), que é um múltiplo de 3.

Como cada um dos três subconjuntos tem n elementos, esse processo de seleção nos fornece um total de escolhas possíveis.
Outra forma de conseguir 3 números distintos cuja soma seja múltiplo de 3, é escolher um número em cada subconjunto. Com em cada subconjunto existem n elementos, esse processo nos fornece n x n x n = n³ escolhas possíveis.Nenhuma outra escolha irá produzir um múltiplo de 3, logo, o total de escolhas possíveis é

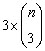+ n³ .

(Adaptada de soluções enviadas por diversos leitores.)

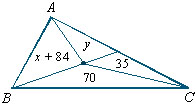
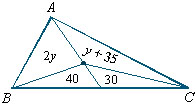
223. Na figura os números indicam as áreas dos triângulos parciais. Qual a área total?

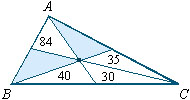
Solução
A área do triângulo ABC é igual a x + y + 189.

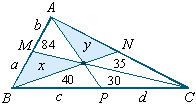
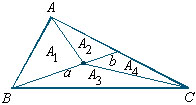
Os triângulos de áreas A₁ e A₂ têm, respectivamente, bases a e b e mesma altura em relação à essas bases, o mesmo ocorrendo com os triângulos de áreas A₃ e A₄. Logo, podemos afirmar que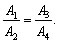
No triângulo do problema temos, então: 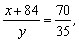o que implica

x + 84 = 2y. (1)

Por outro lado,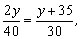 o que implica y = 70. De (1) vem x = 56.

Logo, a área do triângulo ABC é igual a 56 + 70 + 189 = 315.

(Solução enviada por J. Cláudio M. Veloso, RJ.)

224. Dado k inteiro, k > 1, considere 2k bolas brancas e 2k bolas pretas alinhadas numa ordem qualquer. Mostre que existe uma seqüência de 2k bolas consecutivas na qual o número de bolas pretas é igual ao número de bolas brancas.

Solução

Seja 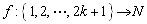a função definida por: “ f (i) é o número de bolas brancas presentes na sequência de 2k bolas consecutivas, tais que a primeira bola está na posição i ”.
Se f (1) = k, as primeiras 2k bolas satisfazem a condição do enunciado.
Se f (1) > k, então f (2k + 1) < k e como
f (i + 1) = f (i) + , com = 0, 1, -1,
segue que f assume todos os valores entre f (2k + 1) e f (1), existindo, portanto, i tal que f (i) = k.
Para f (1) < k, a solução é análoga.

(Solução enviada por Trajano Nóbrega Neto, SP.)

225. Imagine dois segmentos de reta desenhados em uma folha de papel e tais que suas retas suporte se cortam num ponto fora da folha. Seja P um ponto qualquer da folha de papel. Descreva e justifique um método para traçar a reta que passa por P e pelo ponto de encontro das retas suporte dos segmentos.

Solução
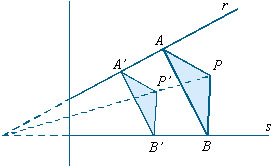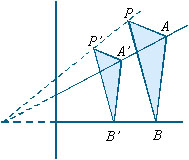
Sejam r e s as retas suportes dos segmentos dados. Tomamos A r e B s, A e B na folha do papel. Construímos um triângulo A’B’P’, com lados paralelos aos lados de ABP, (veja figuras) e A’B’P’ ainda na folha considerada.
Esses triângulos são homotéticos, por uma homotetia de centro no ponto procurado.
A reta 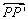é a reta solução.