|
Cláudio Possani
Élvia Mureb Sallum
Flávio Wagner
Rodrigues
IME-USP
Soluções e Sugestões
RPM - Problemas
Caixa
Postal 66281
05311-970 São Paulo, SP
|
|
226.
Uma moeda honesta é lançada até que pela primeira
vez apareçam duas caras em posições consecutivas.
a) Qual é o número máximo
de caras que podem ocorrer em n lançamentos sem que o processo
pare?
b) Quais as probabilidades de que em cinco lançamentos o processo
i) pare no quarto lançamento?
ii) não pare?
227.
Considere a função 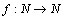 dada
por dada
por  onde
[k] denota o maior inteiro menor ou igual a k. Determine
o conjunto imagem de f. onde
[k] denota o maior inteiro menor ou igual a k. Determine
o conjunto imagem de f.
(Extraído do livro Problem-solving strategies de
A. Engel.)
228.
Dado um triângulo obtusângulo, é sempre possível
dividí-lo em um número finito de triângulos acutângulos?
Se for possível qual é o número mínimo necessário
de triângulos? Justifique sua resposta.
A figura abaixo ilustra uma tentativa que não deu certo...

(Tirado do livro My best Mathematical and Logic Puzzles,
de Martin Gardner.)
229. As equações
das circunferências C1 e C2
da figura são, no plano cartesiano, respectivamente: 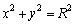 e e
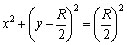 . .
A circunferência C3 é tangente ao eixo
x à C1 e à C2. A
circunferência C4 é tangente à
C1, C2 e C3.
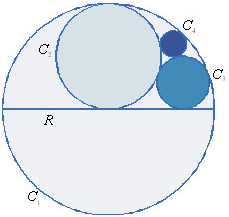
Determine, apenas em função de
R, as coordenadas do centro e o raio da circunferência C4.
(Enviado por Adriano Rocha Pereira, São Paulo, SP.)
1. A mãe de Ana Margarida
vende doces e pediu-lhe que embrulhasse 2003 brigadeiros de 5 cores diferentes em pacotes de 3, de forma que em cada pacote os
brigadeiros fossem da
de 5 cores diferentes em pacotes de 3, de forma que em cada pacote os
brigadeiros fossem da  mesma
cor. Como recompensa prometeu-lhe que poderia comer todos os brigadeiros
que restassem quando já não fosse possível fazer
mais pacotes.Quantos brigadeiros, no máximo, poderá a Ana
Margarida comer? mesma
cor. Como recompensa prometeu-lhe que poderia comer todos os brigadeiros
que restassem quando já não fosse possível fazer
mais pacotes.Quantos brigadeiros, no máximo, poderá a Ana
Margarida comer?
(Tirado
do Jornal de Matemática Elementar. Lisboa, dezembro de
2003.)
2.
João, parado na porta de sua casa, conta as pessoas que passam
em ambas as direções. Pedro caminha ida e volta no quarteirão
da casa de João e conta as pessoas com as quais cruza, em ambas
as direções. Quem conta mais?
(Adaptado
do livro Inteligência instantânea de Jaime Poniachik.)
3.
Dispomos de quatro cores distintas e precisamos colorir o mapa da figura
com os países P, Q, R e S, de modo que países cuja
fronteira é uma linha não podem ser coloridos com a mesma
cor. De quantas maneiras é possível colorir o mapa, se:
a)
P e S forem coloridos com cores distintas?
b)
P e S forem coloridos com a mesma cor?
(Vestibular
da UNESP, 2003.)
 Respostas na p. 52.
Respostas na p. 52.
|
Soluções dos problemas propostos na RPM 52 |
218. Dados m e
n inteiros positivos, considere um retângulo, de base m
e altura n,  quadriculado
com coordenadas inteiras. Determine o número de pontos de encontro
da diagonal do retângulo, d, com o quadriculado incluindo
os lados do retângulo original. quadriculado
com coordenadas inteiras. Determine o número de pontos de encontro
da diagonal do retângulo, d, com o quadriculado incluindo
os lados do retângulo original.
Solução
Sejam H = {pontos de d que estão sobre alguma horizontal
do quadriculado} e V = {pontos de d que estão sobre alguma
vertical do quadriculado}
Se A é um conjunto finito de pontos, usaremos a notação
| A | para indicar o número de elementos de A.
O número de pontos procurado é igual a:
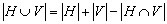
Aplicando o resultado do artigo Como
obter o MDC e o MMC sem fazer contas? (RPM
51, p. 29-31) temos  e,
como e,
como  e e
 segue segue
(Solução
adaptada da enviada por Marcelo Polezzi.)
219. Dados x e
y números inteiros positivos, mostre que, se  é
divisível por 10, então é divisível por 100. é
divisível por 10, então é divisível por 100.
Solução
Se 10 divide  ,
então 2 divide ,
então 2 divide  ;
logo, ;
logo,  é
par, implicando x e y pares, o que, por sua vez, implica é
par, implicando x e y pares, o que, por sua vez, implica
 múltiplo
de 4. Se 10 divide múltiplo
de 4. Se 10 divide  ,
então 5 divide ,
então 5 divide  . .
Se mostrarmos que isso implica x e y múltiplos
de 5, teremos que 25 dividirá  ,
que é múltiplo de 4, logo 100 dividirá ,
que é múltiplo de 4, logo 100 dividirá  . .
Prova de que x e y são múltiplos
de 5
Escrevendo  com
a, b, c e d inteiros não negativos e com
a, b, c e d inteiros não negativos e  obtemos obtemos
 
Como 5 divide  ,
temos que 5 divide ,
temos que 5 divide 
Se  temos temos
 que
não é múltiplo de 5, já que b =1, 2, 3 ou
4. que
não é múltiplo de 5, já que b =1, 2, 3 ou
4.
Se  fazendo
todas as possíveis substituições para b
e d em fazendo
todas as possíveis substituições para b
e d em  ,
obtemos: ,
obtemos:
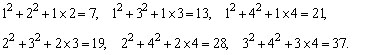
Como nenhum dos resultados é divisível por 5, concluímos
que b = d = 0 e, portanto, x e y são múltiplos de 5.
(Solução de Sérgio
dos Santos Correia Jr., RJ.)
 220.
Considere duas retas paralelas que distam a entre si e um quadrado ABCD,
de lado a, situado no plano das paralelas numa posição tal
que os vértices A e C estejam em lados opostos
do plano dividido pela faixa das paralelas. 220.
Considere duas retas paralelas que distam a entre si e um quadrado ABCD,
de lado a, situado no plano das paralelas numa posição tal
que os vértices A e C estejam em lados opostos
do plano dividido pela faixa das paralelas.
Calcule a soma dos perímetros dos triângulos sombreados.
Solução
Consideremos o quadrado MNPQ, com lados paralelos
às retas paralelas dadas e contendo os vértices ABCD,
como na figura. Se  é o ângulo indicado, então
é o ângulo indicado, então
DQ = asen e MD = acos
e MD = acos . .
Logo, a medida dos lados do quadrado MNPQ é igual a
asen + acos + acos . .
Indicando por z e z´ as hipotenusas dos triângulos
som-breados e por h e h´ as alturas desses triângulos,
temos:

221. Denotando por
[x] o maior inteiro menor ou igual a x, determine para que
valores de x cada uma das igualdades abaixo é verdadeira:
a) 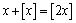 b) b) 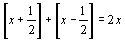 c) c) 
Solução
a) É fácil ver que a igualdade x + [x]
= [2x] vale para todo x inteiro. Por outro lado, se
a igualdade é verdadeira, então x = [2x]
- [x] terá que ser um inteiro, pois é a diferença
de dois números inteiros. Segue que a igualdade é verdadeira
se e somente se x for um número inteiro.
b) Se a igualdade dada em b) for verdadeira, 2x será um
número inteiro pois ele será igual à soma de dois
inteiros. Conclui-se pois que ou x é inteiro ou  com
k inteiro. com
k inteiro.
Para x inteiro  e e  e, portanto, e, portanto,

Para  , , 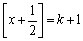 e e  Segue-se que Segue-se que 
Conclui-se que a igualdade b) é verdadeira se e somente se 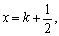 com k inteiro. com k inteiro.
c) Qualquer que seja o número real x, ele pode ser representado
pela soma 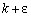 ,
onde k é inteiro e ,
onde k é inteiro e 
i) Suponha 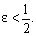 Então,
Então, 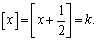
Por outro lado,  e
a igualdade é verdadeira. e
a igualdade é verdadeira.
ii) Suponha,  Então,
Então, 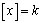 e
e  Por
outro lado, Por
outro lado, 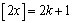 e a igualdade é verdadeira. Segue-se que c) vale para todo
e a igualdade é verdadeira. Segue-se que c) vale para todo 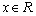 . .
(Adaptado da solução enviada
por Sérgio dos Santos Correia Jr., RJ.)
 Por outro lado, Por outro lado,  e e  . Sendo x, y, x´ e y´
os catetos indicados na figura, temos . Sendo x, y, x´ e y´
os catetos indicados na figura, temos
 e
e  o
que implica o
que implica 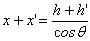
 e
e  o que implica
o que implica 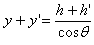
A soma, s, dos perímetros dos triângulos
sombreados será:
s = x + x´+ y + y´
+ z + z´


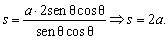
(Solução enviada pelo leitor
J. Claudio M. Velloso, RJ)
Algumas das soluções
enviadas por leitores assumiram que o quadrado estava numa posição
particular, ou assumiram, a priori, que a soma era constante. Essas
soluções não foram consideradas.
| Relação
dos leitores que enviaram soluções dos problemas da RPM 52 |
|
Adalberto A. Dornelles F., RS: 218, 219 |
J. Cláudio M. Velloso, RJ: 218,219,220 |
|
Amadeu C. Almeida, RJ: 219, 220 |
Milton
Dini Maciel, SP: 218,219,221 |
| Antonio
Matos dos Santos, PR: 218 |
Ricardo T. Gonçalves, SP: 218, 219, 220, 221 |
| Celso
M. Rodrigues, RJ: 219, 220, 221 |
Sérgio dos S.Correia Jr, SP: 218, 219, 220, 221 |
| Fernando
Carvalho Ramos, RS: 221 |
Tsunediro
Takahashi, SP: 221 |
| Francisco
Nery, SP: 218, 219, 220, 221 |
Zilton
Gonçalves. RJ: 220 |
|
Resposta dos ... probleminhas
1. 8
2. Contam o mesmo número
3. a) 48
b) 36 |
|