|
Cláudio Possani
Élvia Mureb Sallum
Flávio Wagner
Rodrigues
IME-USP
Soluções e Sugestões
RPM - Problemas
Caixa
Postal 66281
05311-970 São Paulo, SP
|
|
222. Para n
 1,
determine, em função de n, de quantas maneiras podemos
escolher 3 números distintos no conjunto {1, 2, 3,..., 3n}
de modo que a soma dos números escolhidos seja divisível
por 3. 1,
determine, em função de n, de quantas maneiras podemos
escolher 3 números distintos no conjunto {1, 2, 3,..., 3n}
de modo que a soma dos números escolhidos seja divisível
por 3.
(Generalização
de um problema proposta no livro Análise Combinatória
e Probabilidade da CPM - SBM)
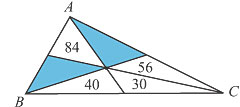
223. Na figura
os números indicam as áreas dos triângulos parciais.
Qual a área total?
(Concurso do IME - Instituto Militar de Engenharia)
224.
Dado k inteiro, k > 1, considere 2k bolas
brancas e 2k bolas pretas alinhadas numa ordem qualquer. Mostre
que existe uma seqüência de 2k bolas consecutivas
na qual o número de bolas pretas é igual ao número
de bolas brancas.
(Enviado por Cláudio Arconcher, Jundiaí,
SP.)
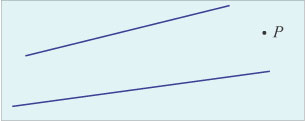
225. Imagine
dois segmentos de reta desenhados em uma folha de papel e tais que suas
retas suporte se cortam num ponto fora da folha.
Seja P um ponto qualquer da folha de papel. Descreva e justifique
um método para traçar a reta que passa por P e
pelo ponto de encontro das retas suporte dos segmentos.
(Enviado por Marcelo
Câmara, Recife, PE.)
1. Evandro e Augusto moram no mesmo edifício.
O número do andar de Evandro coincide com o número do apartamento
de Augusto e a soma dos números dos dois apartamentos é
56. Se cada andar tem 12 apartamentos, numerados de 1 a 12 no primeiro
andar, de 13 a 24 no segundo e assim por diante, quais os números
dos apartamentos de Augusto e Evandro?
(Adaptado
de um problema proposto por Fernando Casagrande.)
2.
Num concurso de televisão três concorrentes procuram acertar
o número de  caramelos
contidos numa taça de cristal. José diz que há 260,
Maria crê que há 274 e Carlota caramelos
contidos numa taça de cristal. José diz que há 260,
Maria crê que há 274 e Carlota  propõe
que sejam 234. Sabe-se que um deles se enganou em 9 caramelos, outro em
17 e outro em 31. Pode-se deduzir qual o número de caramelos na
taça? propõe
que sejam 234. Sabe-se que um deles se enganou em 9 caramelos, outro em
17 e outro em 31. Pode-se deduzir qual o número de caramelos na
taça?
(Tirado
do Jornal de Matemática Elementar, No 218. Lisboa,
setembro de 2003.)
 3.
95% da massa de uma melancia de 10 quilos é constituída
de água. A fruta é submetida a um processo de desidratação
(que elimina apenas a água) até que a participação
da água na massa de melancia se reduz a 90%. Qual é a massa
da melancia após o processo de desidratação? (FUVEST) 3.
95% da massa de uma melancia de 10 quilos é constituída
de água. A fruta é submetida a um processo de desidratação
(que elimina apenas a água) até que a participação
da água na massa de melancia se reduz a 90%. Qual é a massa
da melancia após o processo de desidratação? (FUVEST)
(Ver
respostas na
seção "O leitor pergunta")
|
Soluções dos problemas propostos na RPM 51 |
214.
Considere que no retângulo ABCD, com 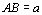 e
e 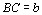 ,
existem duas circunferências ,
existem duas circunferências 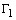 e
e 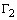 que satisfazem as condições:
que satisfazem as condições:
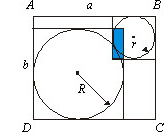
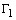 tangente a AB e BC,
tangente a AB e BC, 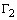 tangente a AD e DC e e tangentes entre si externamente.
Se os quadrados Q1 e Q2,
com lados paralelos aos lados do retângulo ABCD, são
circunscritos a
tangente a AD e DC e e tangentes entre si externamente.
Se os quadrados Q1 e Q2,
com lados paralelos aos lados do retângulo ABCD, são
circunscritos a 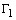 e
e 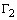 ,
respectivamente, prove que a área de ,
respectivamente, prove que a área de 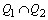 pode ser dada apenas em função de a e b.
pode ser dada apenas em função de a e b.
Solução
Os lados do retângulo 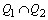 podem
ser calculados em função de a, b, R e r
e são expressos por podem
ser calculados em função de a, b, R e r
e são expressos por
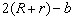 e
e 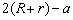 . .
A área é, portanto,
A = [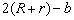 ].[ ].[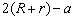 ],
isto é, ],
isto é,
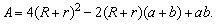
Aplicando o Teorema de Pitágoras ao triângulo
retângulo de lados paralelos aos lados do retângulo ABCD
e que possui os centros das circunferências como vértices,
obtém-se
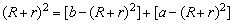 ou ou
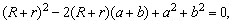 que
tem solução que
tem solução
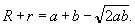
Substituindo esse valor na expressão de A, obtemos a
área em função de a e b escrita
de várias maneiras diferentes. Algumas das expressões enviadas
por nossos leitores são:
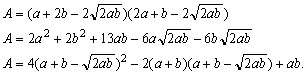
215.
Luís gastou todo o dinheiro que tinha em n lojas. Em cada
loja ele gastou R$1,00 a mais da metade do que tinha ao entrar na loja.
Determine, em função de n, quantos reais ele tinha
ao entrar na primeira loja.
Solução
Para 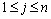 ,
seja ,
seja 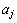 o
número de reais que Luís tinha ao entrar na j-ésima
loja. Como na n-ésima loja ele gastou um real a mais da
metade do que tinha ao entrar e ficou sem nada, segue-se que o
número de reais que Luís tinha ao entrar na j-ésima
loja. Como na n-ésima loja ele gastou um real a mais da
metade do que tinha ao entrar e ficou sem nada, segue-se que 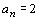 .
O mesmo raciocínio nos permite afirmar que, se ele .
O mesmo raciocínio nos permite afirmar que, se ele 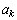 tem reais ao entrar numa loja, ao entrar na loja anterior ele teria
tem reais ao entrar numa loja, ao entrar na loja anterior ele teria 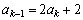 .
Segue-se .
Segue-se 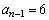 que
e que: que
e que: 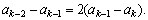
Portanto,
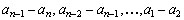 é uma progressão geométrica com
é uma progressão geométrica com 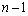 termos cujo primeiro termo é 4 e cuja razão é 2.
A soma dos termos dessa progressão é dada por:
termos cujo primeiro termo é 4 e cuja razão é 2.
A soma dos termos dessa progressão é dada por: 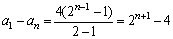 . .
Portanto,
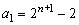 é
o número de reais que Luís tinha ao entrar na primeira loja. é
o número de reais que Luís tinha ao entrar na primeira loja.
(Adaptada de soluções enviadas por vários
leitores.)
216.
Para n > 1, seja 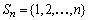 . .
(a) Determine os valores de n para os quais é possível expressar
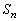 como
a reunião de dois conjuntos disjuntos tais que as somas dos elementos
contidos em cada um deles sejam iguais. como
a reunião de dois conjuntos disjuntos tais que as somas dos elementos
contidos em cada um deles sejam iguais.
(b) Para os valores de n, para os quais a representação
é possível, mostre uma maneira que permita a determinação
dos conjuntos.
Solução
A soma dos elementos de Sn é igual
a 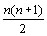 e
o problema terá solução somente quando essa soma
for par, isto é, quando n ou e
o problema terá solução somente quando essa soma
for par, isto é, quando n ou 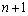 forem
múltiplos de 4. Nesses casos a solução existe sempre
e não é necessariamente única, como se vê para forem
múltiplos de 4. Nesses casos a solução existe sempre
e não é necessariamente única, como se vê para
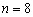 ,
que admite as decomposições: ,
que admite as decomposições:
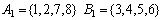
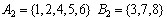
Uma maneira de determinarmos uma solução, quando ela existe,
é encontrar o inteiro k tal que:
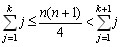 e em seguida observar que
e em seguida observar que
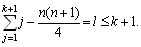
Excluindo l do conjunto 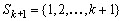 ,
obtemos uma solução. ,
obtemos uma solução.
Observações:
1) A técnica utilizada permite mostrar
também que se,  ,
existe um subconjunto de Sn cuja soma
dos elementos é igual a m. ,
existe um subconjunto de Sn cuja soma
dos elementos é igual a m.
2) Como foi observado por alguns leitores,
uma questão interessante seria determinar quantas soluções
existem para um dado n.
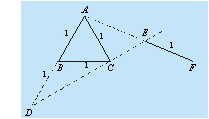 217.
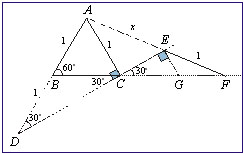
Seja ABC um triângulo equilátero de lado 1, D 217.
Seja ABC um triângulo equilátero de lado 1, D
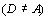 um
ponto na semi-reta um
ponto na semi-reta 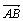 com
BD = 1. Considere os pontos E e F satisfazendo:
A, E e F alinhados, E entre A e F
e sobre a semi-reta com
BD = 1. Considere os pontos E e F satisfazendo:
A, E e F alinhados, E entre A e F
e sobre a semi-reta 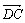 ,
F na semi-reta ,
F na semi-reta 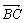 com
EF = 1. Calcule a medida do segmento AE. com
EF = 1. Calcule a medida do segmento AE.
Solução:
Sendo o triângulo BCD isósceles, temos a medida
do ângulo 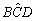 igual a 30°, logo, o ângulo
igual a 30°, logo, o ângulo 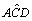 é
reto. Traçamos é
reto. Traçamos 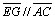 .
Pela semelhança dos triângulos FEG e FAC,
temos .
Pela semelhança dos triângulos FEG e FAC,
temos 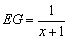 , ,
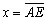 .
Por outro lado, .
Por outro lado,
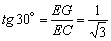 sendo
sendo 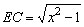 logo,
logo, 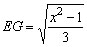 . .
Então, 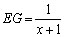 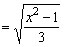 ,
o que implica ,
o que implica 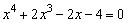 ,
ou seja, ,
ou seja, 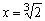 . .
(Solução enviada por Milton Dini Maciel,
SP.)
Observação:
A partir de um segmento unitário, é impossível construir
com régua e compasso um segmento de comprimento 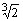 .
Porém, este problema oferece uma maneira prática, usando
uma faixa de papel, de construir tal segmento. Assim, após a construção
de um triângulo equilátero ABC de lado 1 e das semi-retas .
Porém, este problema oferece uma maneira prática, usando
uma faixa de papel, de construir tal segmento. Assim, após a construção
de um triângulo equilátero ABC de lado 1 e das semi-retas
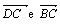 ,
marcamos nas beiradas de uma régua de papel dois pontos E
e F com ,
marcamos nas beiradas de uma régua de papel dois pontos E
e F com 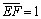 .
Colocando tal régua de modo que passe por A e que .
Colocando tal régua de modo que passe por A e que 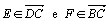 ,
obtemos ,
obtemos 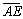 com medida
com medida 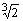 . .
|
Relação dos
leitores que enviaram soluções dos problemas da RPM 50 |
|
Alan Henrique de Sá, RJ: 210, 211 |
João F. Moura, RJ: 210, 211, 212, 213 |
|
Amadeu C. Almeida, RJ: 211, 213 |
João Linneu
A. Prado, SP: 210, 211, 213 |
|
Amaro José de O. Filho, PE: 210,
211 |
Joaquim Ferreira da Silva, PE: 211 |
|
Aníbio
Pacheco, SC: 210, 211 |
José C. M. Veloso, RJ: 210, 211, 212, 213 |
|
Antonio
Ferreira Sobrinho, SP: 211 |
Luiz César Niehues,
SC: 211 |
|
Antonio
Luiz Miranda, RJ: 211 |
Mauro Felix de Sousa, RJ: 210 |
|
Antonio
M. Santos, PR: 210, 211,212,213 |
Rizio SantAna,
MG: 210, 211 |
|
Celso Martinez Rodrigues, MG: 211 |
Roberto Alexandre Loewenberg,
SP: 211 |
|
Clodoaldo Lessa, SP: 210 |
Roberto P. Chagas, MG: 210, 211, 212 |
|
Eduardo Luís Estrada, SP: 210 |
Sebastião Maurício Santos, MG: 210, 211 |
|
Érico Rodrigues Silva, MG: 211 |
Sérgio S. Correia Jr., RJ: 210,
211, 212 |
|
Fernando Carvalho Ramos, RS: 211 |
Tsunediro Takahashi, SP- 211 |
|
Flávio Ricardo L. da Cunha, GO: 211 |
Victor Chakur.SP-210,211 |
|
Florival
Carlos Souza, GO: 210, 211 |
Wanderley
Gambá, SP- 211, 212 |
|
Geraldo Cláudio Broetto,
ES: 210 |
Robério
L. de Carvalho, CE - 210, 211 |
|
Geraldo Perlino
Jr., SP: 211, 212, 213 |
Paulo Sérgio C. Lino.MG-212 |
|
Henrique O. Pires, MG: 210, 211, 212 |
Milton Dini Maciel, SP - 210, 211, 212 |
|
Jaime Oliveira, SE: 211, 212 |
Carl Henning Schinke, RJ |
Nota
da RPM
Na solução do problema 212, publicada na p. 44 da seção
Problemas da RPM 52, há uma frase sem sentido. Trata-se da frase
que começa:
Pela congruência dos triângulos CXP e 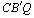 ..., ...,
que deve ser substituída por:
Pela congruência dos triângulos CXP e 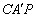 (caso (caso
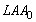 )
e dos triângulos CXQ e )
e dos triângulos CXQ e 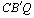 ,
concluímos que ,
concluímos que 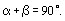
Pedimos desculpas aos nossos leitores pela falha involuntária. |