Concurso
PEB II do Estado de São Paulo 2003
(para
professores de 5ª a 8ª séries e Ensino Médio)
Conhecimento específico - Matemática
|
|
31.
Seja a e b naturais e o mdc(a,b)=17. Sabendo que a > b e a = 238, podemos
afirmar que, nessas condições, o total de valores que b
pode assumir será de:
a) 3 b)
4 c) 5 d)
6 e) 7
32.
Uma forma de iniciar o estudo dos quadriláteros é pedir
aos alunos que os classifiquem, tendo como critérios as suas propriedades
e regularidades. Desta forma, os alunos terão maior compreensão
de cada quadrilátero e das relações existentes entre
eles. Uma possibilidade de apresentar as relações existentes
entre alguns quadriláteros é por meio de conjuntos.
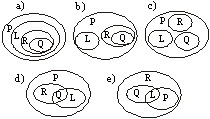
Seja L o conjunto dos losangos, P o
conjunto dos paralelogramos, Q o conjunto dos quadrados,
R o conjunto dos retângulos, a relação
entre eles pode ser representada por:
33.
O gráfico a seguir refere-se à função
f(x) = x2.
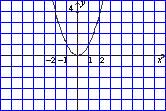
Se
transladarmos o gráfico dessa função, horizontalmente,
três unidades para a direita e, verticalmente, quatro unidades para
baixo, a nova função será:
a)
f(x) = (x + 3)2 + 4
b) f(x) = (x - 3)2 - 4
c) f(x) = (x + 3)2 - 4
d) f(x) = (x - 3)2 + 4
e) f(x) = (x - 4)2 + 3
34.
A escala Richter foi criada nos anos 30 pelo americano Charles Francis
Richter. Nessa escala é medida a magnitude do tremor causado por
um terremoto. A intensidade de um terremoto (I) é definida por
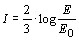 onde
E é a energia liberada pelo terremoto em quilowatt-hora, e E0 equivale
a 10-3 kwh. Se a diferença de intensidade de 2 pontos entre dois
terremotos corresponde a uma liberação de energia x
vezes maior, o valor de x, nesse caso, equivale a: onde
E é a energia liberada pelo terremoto em quilowatt-hora, e E0 equivale
a 10-3 kwh. Se a diferença de intensidade de 2 pontos entre dois
terremotos corresponde a uma liberação de energia x
vezes maior, o valor de x, nesse caso, equivale a:
a) 2 b) 10
c) 100 d) 200
e) 1000
35. Um octógono regular
é formado cortando-se triângulos retângulos isósceles
nos vértices de um quadrado, como mostra a figura a seguir. Se
o lado do quadrado é 1, o comprimento dos catetos dos triângulos
é igual a:
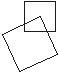
36. Conforme mostra a figura
abaixo, um quadrado grande de 3m de lado tem um de seus vértices
no centro do quadrado pequeno de 1,5m de lado. Dois lados do quadrado
grande cortam dois lados do pequeno, cada um em um terço do lado
do quadrado menor. A área comum aos dois quadrados, em relação
à área do quadrado menor, é igual a:
a) 1/6
b) 2/5
c) 1/4
d) 1/3
e) 1/2 |
 |
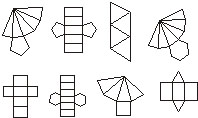
37. As figuras a seguir
representam as planificações de figuras tridimensionais.
As planificações que possuem 2 eixos de simetria são:
a)
cubo, tetraedro e prisma triangular regular
b) pirâmide triangular regular e pirâmide de base pentagonal
c) prisma triangular regular e prisma de base pentagonal
d) tetraedro, pirâmide de base quadrada e pirâmide de base
pentagonal
e) tetraedro, prisma de base quadrada e prisma de base pentagonal
38.
Em uma caixa, o fabricante acondicionou 100 camisetas de três cores
e de três tamanhos diferentes, nas quantidades indicadas na tabela
abaixo.

A probabilidade de uma pessoa retirar dessa caixa uma
camiseta vermelha ou grande é de:
a) 0,34 b) 0,48
c) 0,54
d) 0,68 e) 0,74
39. Em um tabuleiro de xadrez
(tabuleiro 8x8), o total de possibilidades de escolher um quadrado preto
e um quadrado branco de forma que os dois não pertençam
à mesma linha ou à mesma coluna é igual a:
a) 1024 b) 932
c) 800 d) 768
e) 576
40. Se o quociente e o resto
da divisão de um certo número natural por 327 são,respectivamente,
18 e 10, então, o quociente e o resto da divisão do dobro
deste número por 654, nesta ordem, são:
a) 9 e 5 b)
18 e 10 c) 18 e 20
d) 36 e 10 e) 36 e 20
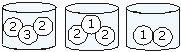
41. Se de cada uma das caixas
retirarmos uma bola, o total de possibilidades de que a soma das três
bolas seja 6 é:
a) 3 b) 5
c) 7 d) 9 e) 11
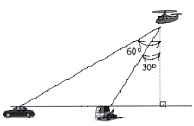
42. Um helicóptero
está a 200 metros de altura, na vertical, sobre uma estrada. Na
posição em que se encontra, o piloto do helicóptero
enxerga um carro quebrado em uma direção que forma 60º
com a vertical e, na mesma estrada, um guincho em uma direção
de 30º com a mesma vertical, conforme o desenho abaixo. Sabendo que
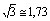 ,
a distância aproximada entre o carro quebrado e o guincho, nesse
momento, é igual a: ,
a distância aproximada entre o carro quebrado e o guincho, nesse
momento, é igual a:
a) 230 m b) 270 m
c) 320 m
d) 340 m e) 380 m
43. O IDH – Índice
de Desenvolvimento Humano – é um número entre 0 e
1, calculado pela média aritmética de três índices:
de educação, de expectativa de vida ao nascer e do PIB em
dólares. Com base nesses dados e na comparação entre
os países, é possível analisar a qualidade de vida
e o desenvolvimento humano no planeta. O cálculo do índice
do PIB é feito através da seguinte fórmula:
Índice do

onde PIB per capita é o valor da renda
per capita do país analisado, em dólar; U$40 000 é
o valor máximo de renda per capita no mundo.
Um país que tenha o índice do PIB igual a 0,79, possui um
PIB per capita aproximado de:
a) U$ 100
b) U$ 500
c) U$ 1 000
d) U$ 5 000
e) U$ 10 000.
(Dados: log20,30; log30,48; log50,70.)
44. O
gráfico abaixo mostra os recordes obtidos pelas mulheres e pelos
homens, na corrida de 100 metros.

A menor diferença entre os recordes masculino e feminino ocorreu
entre os anos:
a) 1972 e 1977 b) 1977 e 1984
c) 1984 e 1991 d) 1991 e 1996
e) 1996 e 2002
45. Ao longo da História
da Civilização muitos povos, como os egípcios, romanos,
maias, babilônios, entre outros, criaram diferentes sistemas de
numeração que auxiliaram seu desenvolvimento. O sistema
de nume-ração decimal, apesar do longo tempo para ser difundido
e aceito, é hoje o mais utilizado no mundo. Comparando-se as características
do sistema de numeração decimal e do romano, podemos dizer
que ambos:
a) são sistemas posicionais.
b) possuem o princípio aditivo.
c) possuem os princípios subtrativo e multiplicativo.
d) possuem um símbolo para o zero.
e) repetem no máximo três vezes os seus algarismos.
47. Em um artigo da Revista
do Professor de Matemática, o professor Elon Lages Lima justifica
a importância do estudo de sistemas lineares e discute o equívoco
em se utilizar a Regra de Cramer para discutir se um sistema é
possível ou impossível. Dessa forma, o professor aconselha
a resolver sistemas por escalonamento ou interpretação geométrica.
No artigo, o professor Elon cita o sistema:

Pode-se afirmar que o sistema é:
a) impossível.
b) possível e indeterminado.
c) possível e determinado com uma solução nula.
d) possível e determinado com o produto das soluções
igual a 28.
e) possível e determinado com a soma das soluções
igual a 15.
48. O diâmetro
da Lua é aproxi-madamente um quarto do diâmetro da Terra.
A razão entre o volume da Terra e o volume da Lua é, aproximadamente:
a) 64 b) 32
c) 16
d) 8 e) 4
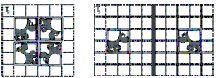
49. Observe que a figura
A sofreu algumas transformações .
|


|
Na ordem, as transformações
ocorridas foram de:
a) translação – reflexão – rotação
b) translação – rotação –
reflexão
c) reflexão – rotação – translação
d) reflexão – translação – rotação
e) rotação – translação –
reflexão
|
50. Mauro
foi convidado por seu amigo para dar uma palestra em uma escola no interior
de São Paulo. Como seu amigo sempre gostou de Matemática,
decidiu, utilizando coordenadas cartesianas, elaborar o mapa do local
onde aconte-ceria o evento. Como brincadeira, seu amigo enviou o mapa,
substituindo uma informação por um desenho. Veja o fax que
Mauro recebeu.


O ponto inicial a que o amigo de Mauro se referia é o ponto:
a) N b) P
c) R d) S
e) T
51. Um professor pediu a
seus alunos a leitura do problema e da demons-tração feita.
Solicitou que justificassem as últimas afirmações.
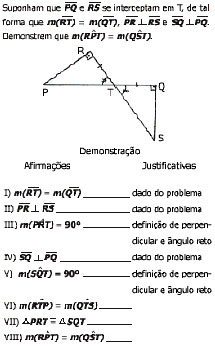
As justificativas VI, VII e VIII, respectivamente, são:
a) ângulos perpendiculares - caso LAL -
ângulos correspondentes de triân-gulos congruentes.
b) ângulos perpendiculares - caso ALA - ângulos correspondentes
de triân-gulos congruentes.
c) ângulos opostos pelo vértice - caso LAL - ângulos
correspondentes de triângulos congruentes.
d) ângulos opostos pelo vértice - caso ALA - ângulos
correspondentes de triângulos congruentes.
e) ângulos opostos pelo vértice - caso LLL - ângulos
correspondentes de triângulos congruentes.
52.
Uma das formas de extrair a raiz quadrada é através de aproximações
sucessivas. Veja uma explicação dada pelo professor Mário
Barone Júnior: “Para obter a 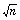 ,
começamos com uma primeira aproximação a1
escolhida de modo qualquer. A menos que n seja
um quadrado perfeito (o que não é comum), tem-se, em geral, ,
começamos com uma primeira aproximação a1
escolhida de modo qualquer. A menos que n seja
um quadrado perfeito (o que não é comum), tem-se, em geral,
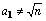 .
Então, um dos dois números a1
, .
Então, um dos dois números a1
, 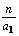 é
menor do que é
menor do que 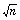 ,
e o outro é maior. A média aritmética ,
e o outro é maior. A média aritmética 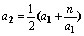 é,
neste caso, uma aproximação para é,
neste caso, uma aproximação para 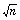 ,
melhor do que a1 ....”. De
acordo com essa explicação, se fôssemos extrair, através
desse método, a raiz quadrada de 86, poderíamos, por exemplo,
ter a1= 9. Dessa
forma: n = 86, a1=
9 e ,
melhor do que a1 ....”. De
acordo com essa explicação, se fôssemos extrair, através
desse método, a raiz quadrada de 86, poderíamos, por exemplo,
ter a1= 9. Dessa
forma: n = 86, a1=
9 e 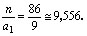 A
diferença entre a2 calculado
e o valor obtido na calculadora é de: A
diferença entre a2 calculado
e o valor obtido na calculadora é de:
a)
0,004 b) 0,015
c) 0,058
d) 0,093 e) 0,101
53. Observe a figura:
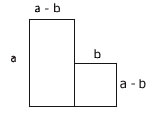
Essa
representação geométrica corresponde à expressão
algébrica:
a)
o quadrado da soma de dois termos
b) o quadrado da diferença de dois termos
c) a soma dos quadrados de dois termos
d) a diferença dos quadrados de dois termos
e) o produto de dois termos
54. As figuras abaixo, respectivamente,
são as construções relativas ao vértice A
da:
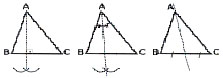
a) altura – mediana – bissetriz interna
b) altura – bissetriz interna – mediana
c) mediana – bissetriz interna – altura
d) mediana – altura – bissetriz interna
e) bissetriz interna – altura – mediana
55. Em um jogo, cada participante
recebe um total de fichas azuis correspondente ao valor obtido, quando
se joga o dado. Quando o jogador tiver em mãos 5 fichas azuis,
deverá trocar por 1 ficha verde. Com 5 fichas verdes, o jogador
deverá trocar por 1 preta e, finalmente, 5 pretas, por 1 branca.
Se um jogador juntar suas fichas azuis sem trocá-las, a quantidade
necessária dessas fichas para obter uma ficha branca será
de:
a) 125 b) 65
c) 45
d) 25 e) 5
56. Um
banco ofereceu a seus clientes um novo tipo de senha para o acesso da
conta corrente, composta por quatro dígitos. A senha deve ser formada
a partir dos conjuntos das 26 letras do alfabeto e dos algarismos do sistema
decimal (0 a 9), sem repetição. As letras e os algarismos
devem ser intercalados, ou seja, não pode haver duas letras juntas
ou dois algarismos juntos. O número máximo de senhas que
podem ser criadas neste sistema é:
a) 67 600
b) 98 500
c) 109 512
d) 117 000
e) 135 200
59. Uma empresa resolveu
divulgar um evento pela internet. Para isso enviou uma mensagem por e-mail
para 2 pessoas, as quais deveriam retransmiti-la a outras 2 pessoas no
dia seguinte, e assim por diante. Suponha que esse processo tenha sido
seguido à risca pelas pessoas, sempre enviando a mensagem para
outras 2 pessoas no dia seguinte. Em uma semana, o número total
de pessoas que terá recebido essa mensagem será de:
a) 14 b) 49
c) 126
d) 254 e) 508
60. Considerando o conjunto
de pontos a seguir:
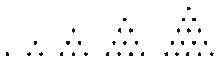
pode-se dizer que é uma seqüência numérica cuja
lei de formação correspondente é:
a) 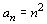
b) 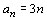
c) 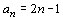
d) 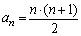
e) 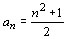
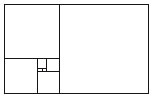
61. A figura abaixo é
composta por quadrados. Se os dois quadrados menores têm lado 1,
então a área total da figura será:
a) 441
b) 625
c) 714
d) 1024
e) 1156 |
 |
62. Em uma determinada época,
o dólar estava sendo cotado a R$ 3,20 no mercado de câmbio,
ou seja, US$1=R$3,20. Se houver uma valorização do real
em relação ao dólar de 25%, então podemos
afirmar que:
a) o dólar sofrerá uma desvalorização
de 20%.
b) o dólar sofrerá uma desvalorização de 30%.
c) a cotação do dólar passará a ser de R$
2,40.
d) a cotação do dólar passará a ser de R$
3,00.
e) a cotação do dólar passará a ser de R$
4,00.
63. A área
da região limitada pela interseção das inequações
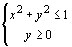 é é
a)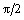 b)
b)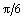 c)
c)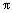 d)
d) 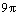 e)
e) 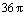
64. Com o objetivo de ensinar
o significado das operações com matrizes a seus alunos,
um professor propôs a seguinte discussão: analisando a tabela
de classificação da última Olimpíada (Tabela
1), verificou-se uma distorção entre a posição
de alguns países e o número total de medalhas obtidas. Isso
acontece em função de um critério de classificação
que beneficia sempre “o melhor”, não considerando fatores
como diversidade de modalidades, número total de medalhas, etc...
Uma forma de contornar essa situação seria considerar o
número total de medalhas obtidas por cada país com pesos
diferenciados (ver Tabela 2).
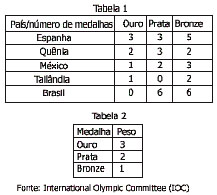
A partir das tabelas fornecidas, o professor propôs
a construção de uma nova tabela que forneça o total
de pontos obtidos por cada país pelo novo critério, envolvendo
uma operação entre matrizes. A respeito da nova classifi-cação
obtida, podemos afirmar que:
a) a pontuação do Brasil seria superior
à do Quênia, México e Tailândia.
b) a pontuação do Brasil seria inferior apenas à
do Quênia e da Espanha.
c) o Brasil estaria melhor colocado, em relação aos demais
países, por obter o maior número de medalhas.
d) a classificação geral não se alteraria devido
ao maior peso das medalhas de ouro.
e) a pontuação do México seria inferior apenas à
do Brasil e da Espanha.
65. Na disputa de um jogo
de pôquer, utilizam-se 32 cartas do baralho, sendo 8 de cada naipe
(do 7 ao Ás). São distribuídas cinco cartas para
cada jogador. A probabilidade de um jogador receber 3 Ases é:
a)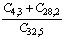 b)
b) 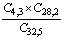
c)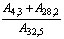 d)
d)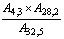
e)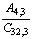
67. A razão entre
o número de anagramas das palavras COSSENO e SECANTE é:
a) 1/2 b) 2/3
c) 1/4
d) 3/4 e) 4/5
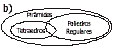
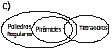
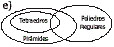
68.Qual
dos diagramas representa os argumentos a seguir?
Alguns tetraedros são regulares.
Todos os tetraedros são pirâmides.
Logo, algumas pirâmides são regulares.


69. A equação
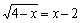 em
R: em
R:
a) admite duas soluções.
b) admite apenas uma solução.
c) não admite soluções.
d) admite uma solução irracional.
e) admite mais de duas soluções.
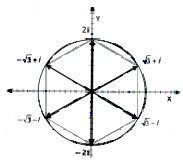
70. Os afixos das n raízes
enésimas de um número complexo Z podem ser representados
geometricamente no plano de Argand-Gauss. Os pontos representados correspondem
às raízes do complexo:
a)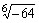 b)
b) c)
c)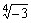 d)
d)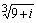 e)
e)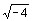
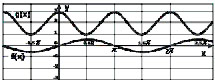
71. Os gráficos abaixo
correspondem às seguintes funções trigonométricas
:
a)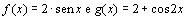
b)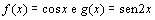
c)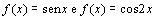
d)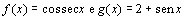
e)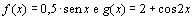
72. O resto da divisão
do polinômio
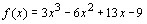 por por
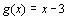 é: é:
a) 81 b) 57
c) 9 d) 3
e) -3
73. No mundo da imaginação,
a idéia de reduzir ou ampliar o tamanho do corpo humano aparece
com freqüência, tanto no cinema como na literatura.
Imaginemos então que exista uma máquina
capaz de ampliar ou reduzir (por homotetia) as dimensões (comprimentos)
do corpo humano em até cinco vezes. Considere que a sustentação
óssea do corpo humano varie proporcionalmente à área
da seção transversal dos ossos, e o peso varie proporcionalmente
ao volume do corpo. Então, podemos afirmar que:
a) não haveria problemas na redução
ou ampliação do corpo, uma vez que todas as dimensões
variam proporcionalmente.
b) somente haveria problemas na redução, uma vez que a estrutura
óssea não sustentaria o peso do corpo.
c) a ampliação seria inviável, uma vez que a massa
cresceria cinco vezes mais do que a capacidade de sustentação
do corpo.
d) a redução implicaria um corpo mais denso, e, portanto,
com uma massa muscular cinco vezes maior que o tamanho do corpo.
e) a ampliação implicaria um corpo mais denso, uma vez que
a massa cresceria cinco vezes mais do que a altura.
74. Dados os conjuntos 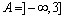 e e
 podemos
afirmar que: podemos
afirmar que:
a) 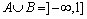
b) 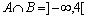
c) 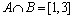
d) 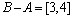
e) 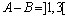
75. Um
professor pediu a seus alunos que efetuassem o cálculo mental do
produto 15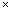 13.
Solicitado a descrever o processo utilizado para se chegar ao resultado,
um dos alunos disse: primeiro multipliquei 15 por 10, obtendo 150. Depois
multipliquei 15 por 3, obtendo 45. Somei 150 com 45 obtendo 195. A propriedade
aritmética que fundamenta esse processo é: 13.
Solicitado a descrever o processo utilizado para se chegar ao resultado,
um dos alunos disse: primeiro multipliquei 15 por 10, obtendo 150. Depois
multipliquei 15 por 3, obtendo 45. Somei 150 com 45 obtendo 195. A propriedade
aritmética que fundamenta esse processo é:
a) comutativa da adição.
b) decomposição em fatores primos.
c) associativa da multiplicação.
d) distributiva da multiplicação em relação
à adição.
e) comutativa da multiplicação.
76. A informação
armazenada em computadores tem como unidade de medida o byte. Seus múltiplos
são o kilobyte, que equivale a 210 bytes, e o megabyte,
210 kilobytes. Assim, um arquivo de tamanho 2 megabytes equivale
exatamente a:
a) 2 000 bytes.
b) 2 000 kilobytes.
c) 210 kilobytes.
d) 211 bytes.
e) 221 bytes.
77. O número de lados
de um polígono regular cujo ângulo interno mede 168°
é:
a) 12 b) 20
c) 30
d) 36 e) 40
78. A passagem conjunta
de dois cometas pela Terra acontece a cada 2 280 anos. Se o período
de um deles é de 120 anos, então o período do outro
poderia ser de:
a) 21 anos.
b) 55 anos.
c) 76 anos.
d) 144 anos.
e) 187 anos.
79. A taxa de inflação
corresponde à variação percentual ponderada dos componentes
de um índice de preços em um determinado período.
Em um certo mês, a taxa de inflação foi de 0,8%. A
tabela, a seguir, mostra a composição do índice e
a variação média dos preços de cada item ocorridas
neste mês.
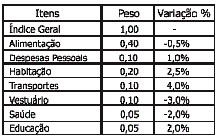
A partir da análise dos dados da tabela, podemos
afirmar que:
a) a contribuição do item educação
na taxa de inflação foi de 0,2%.
b) a contribuição do item vestuário na taxa de inflação
foi de –0,2%.
c) o item que apresentou a menor contribuição para a alta
da inflação foi saúde.
d) o item que mais contribuiu para a alta da inflação foi
transportes.
e) o item que mais contribuiu para a alta da inflação foi
habitação.
80. A equação
da reta, que tangencia a parábola de equação
y = x 2 - 12x + 32 , no ponto (4, 0)
é:
a) y = 3x + 12
b) y = - 4x + 16
c) y = 4x - 32
d) y = - 2x + 8
e) y = x - 4
As questões 46, 57, 58 e 66 foram anuladas.
|