Daniel dos Santos Costa

Esta foi uma atividade desenvolvida com meus alunos da 5ª série de um colégio particular de Brasília e que envolveu as disciplinas de Matemática e Português. Foi uma brincadeira de amigo oculto, com 3 semanas de intervalo entre o sorteio e a revelação.
O objetivo da atividade foi reforçar o estudo dos sólidos geométricos e de suas propriedades e desenvolver a capacidade de redigir textos matemáticos.

A face matemática da atividade consistiu na construção dos presentes (sólidos geométricos), na descrição de algumas de suas propriedades e na resolução de problemas propostos no dia da revelação.
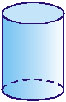
Cada aluno construiu o seu presente, que constou de um cartão e dois sólidos: um era um cone ou um cilindro e o outro era um prisma ou uma pirâmide de base retangular. A construção desses sólidos foi trabalhada na aula de Matemática,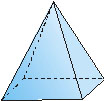 com papel ou sabão. O presente foi embalado numa caixa em forma de paralelepípedo (caixa de camisa, sapatos, etc.) atado com um laço. Foi preciso calcular as dimensões dos sólidos para que coubessem na caixa escolhida e, em sala, no dia da revelação, calcular o tamanho do barbante para fazer o laço na caixa. Cada aluno recebeu o pedaço de barbante do tamanho que ele próprio solicitou.
Alguns calculavam mal e não conseguiam dar o laço, outros precisavam cortar a sobra que era muito grande.

O cartão que acompanhou o presente contava ao amigo algumas das propriedades do presente que ele estava ganhando (número de faces, vértices, etc.). Essa descrição foi trabalhada nas aulas de Português.

Depois de revelados os amigos e entregues os presentes, cada aluno fez o desenho da vista superior, lateral e frontal do presente que ganhou. Teve ainda que resolver alguns problemas propostos, como dar os nomes dos sólidos, calcular número de vértices, faces e arestas do prisma ou pirâmide (verificando a relação de Euler) e fazer algumas medidas no cone ou cilindro.

No final da atividade, os alunos deram sua opinião: acharam interessante, divertida, diferente, embora para alguns ela tenha sido um tanto complicada e trabalhosa.
Fica a idéia.

Curiosidade

O valor de x que verifica a equação abaixo comprova isso.

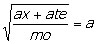
Elevando ao quadrado ambos os membros da igualdade, temos:

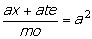, o que leva a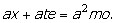

Transpondo a parcela ate para o outro lado da igualdade e dividindo-se todos os termos por a, que é suposto diferente de zero, obtemos o resultado:

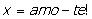
Do Jornal de Matemática Elementar, N. 220, Novembro de 2003. Lisboa, Portugal.