| Fausto
Arnaud Sampaio
Proponho,
neste artigo, uma forma de complementar o ensino do tema fatoração,
estabelecendo conexões com seqüências, extração
de raízes quadradas, e o uso de um algoritmo que pode ser implementado
em um ábaco convencional.
Em 1643, Mersenne enviou a Fermat o desafio
de fatorar o número 100 895 598 169, uma tarefa bastante árdua,
se levarmos em consideração os recursos então disponíveis
para a execução rápida de cálculos. Fermat
resolveu o problema utilizando um método sistemático, baseado
na procura de números x e y tais que:

sendo N o número a ser fatorado.
Como veremos adiante, essa identidade leva a um algoritmo que, apesar
de ainda envolver cálculos trabalhosos, simplificou suficientemente
o problema para permitir a Fermat vencer o desafio.
Observe, inicialmente, que todo número
ímpar é a diferença de dois quadrados. Por exemplo,
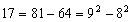
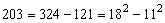
 ,
etc. ,
etc.
A  igualdade
mostra que a afirmação acima é sempre verdadeira,
pois qualquer ímpar é um produto de dois ímpares
e, se a e b são ímpares, os números
entre parênteses são inteiros. igualdade
mostra que a afirmação acima é sempre verdadeira,
pois qualquer ímpar é um produto de dois ímpares
e, se a e b são ímpares, os números
entre parênteses são inteiros.
O problema de fatorar o número ímpar N consiste,
então, em achar x e y tais que  . .
A idéia central do método de Fermat é começar
com x igual ao menor inteiro maior ou igual a 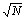 e calcular
e calcular  .
Se o resultado for um quadrado perfeito, o problema está resolvido.
Se não, repete-se o processo, sucessivamente, para os números
x + 1, x + 2, ..., até encontrar um quadrado
perfeito. .
Se o resultado for um quadrado perfeito, o problema está resolvido.
Se não, repete-se o processo, sucessivamente, para os números
x + 1, x + 2, ..., até encontrar um quadrado
perfeito.
1) Fatorar 133.
N = 133 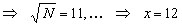

Então,
 . .
2) Fatorar 407.
N = 407 

Então,  . .
Sugerimos que o leitor fatore mais alguns números ímpares
(pequenos) para pegar o jeito.
Observações:
1) Um aluno de 5a série,
tendo em mãos uma calculadora, seria capaz de usar esse algoritmo.
Certamente trata-se de uma alternativa interessante para fatorar um número.
2) Para números muito grandes, calcular
 torna-se
muito trabalhoso. Fermat usou um algoritmo recursivo, que veremos adiante,
para evitar esses cálculos. torna-se
muito trabalhoso. Fermat usou um algoritmo recursivo, que veremos adiante,
para evitar esses cálculos.
3) O processo pode ser muito demorado. Usado
para  ,
exige o cálculo de ,
exige o cálculo de  até
432. Mas, na pior das hipóteses, acaba para até
432. Mas, na pior das hipóteses, acaba para  porque, sempre, porque, sempre,
 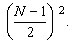 Isso
acontece quando N é um número primo. Isso
acontece quando N é um número primo.
Um outro jeito bom de explorar o método de Fermat é utilizá-lo
em um ábaco.
Suponha que um certo número, 21, por exemplo, seja
fatorado como um produto de dois números ímpares,
 .
Podemos entender essa multiplicação como sendo composta
pela soma repetida  ou
por uma de termos de uma P.A., como 
Escolhemos deliberadamente uma P.A. composta por números
ímpares sucessivos, pois a soma dos n primeiros
ímpares é  Assim,
poderemos estabelecer uma relação entre a identidade
envolvendo a diferença entre |
|
quadrados 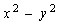 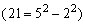 ,
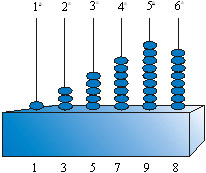
e as fichas nas várias colunas do ábaco representando
as parcelas ímpares, no caso, 5, 7 e 9 fichas. ,
e as fichas nas várias colunas do ábaco representando
as parcelas ímpares, no caso, 5, 7 e 9 fichas.
Vemos ainda que na multiplicação 7 x 3
será 7 o elemento central da soma, e 3 o número de parcelas:
5 + 7 + 9 .
Assim, para fatorar um número ímpar usando fichas, basta
encontrar uma configuração dessas, com a quantidade de
fichas na coluna central do ábaco correspondendo a um dos fatores,
e o número de colunas utilizadas sendo o outro fator.
Mas, como encontrar essa configuração?
 |
Uma vez
que a fatoração de um número implica encontrar
uma soma conveniente de ímpares, comecemos exprimindo-o
como uma soma de 1 + 3 + 5 = ... fichas no ábaco,
e, em seguida, buscaremos um novo arranjo das fichas até
chegarmos à configuração desejada, como mostra
o exemplo abaixo para 
|
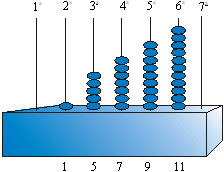 |
Como a 6ª
coluna do ábaco deveria conter 11 fichas para serem a soma
de ímpares sucessivos, a completaremos com as fichas que
faltam, remanejando as 4 primeiras fichas da 1ª e 2ª
colunas. |
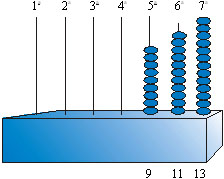 |
Seguindo a mesma idéia, precisamos completar a coluna
seguinte. Para isso, retiramos peças das 3 primeiras colunas.
Agora obtivemos uma seqüência de ímpares suces-sivos.
Assim, temos:
elemento central: 11;
número de termos: 3. |
Portanto, 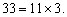
Resta apenas observar que esse procedimento equivale ao processo de
Fermat. Uma vez que estamos remanejando fichas das colunas em ordem
crescente de ímpares, quando o processo leva a uma seqüência
de ímpares sucessivos, iniciada na coluna m (5ª,
na figura) e finalizada na coluna  (7ª,
na figura), a soma das fichas sempre poderá
ser escrita como a diferença de (7ª,
na figura), a soma das fichas sempre poderá
ser escrita como a diferença de  e e
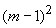 ( ( na figura).
na figura).
No exemplo acima, compare o processo de Fermat e o uso do ábaco: ; x = 6. ; x = 6.
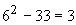 (no
ábaco faltam 3 fichas na coluna com 8 para atingir 11); (no
ábaco faltam 3 fichas na coluna com 8 para atingir 11);
 (somando-se
as 3 fichas anteriores com as 13 que faltaram na 2ª etapa, obtemos
16, portanto (somando-se
as 3 fichas anteriores com as 13 que faltaram na 2ª etapa, obtemos
16, portanto  ). ).
Assim, o uso do ábaco nada mais é do que a utilização
do método de Fermat sob outra forma!
Finalmente, o ábaco fornece todas as fatorações
possíveis de 2 fatores. Por exemplo, se tomarmos o número
45, usando o ábaco obtemos:
(1 + 3 + 5 + 7 + 9 + 11 + 9)
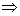 (5
+ 7 + 9 + 11 + 13) = 9.5 (5
+ 7 + 9 + 11 + 13) = 9.5
Se prosseguirmos desse ponto em diante, completando a próxima
coluna com 15 fichas retiradas das colunas com 5,7 e 9, obteremos:
(5 + 7 + 9 +11 +13)
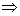 (6 +11+13
+15) (6 +11+13
+15) 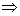 (13 +15 +17)
= 15 x 3 (13 +15 +17)
= 15 x 3
Como vimos, para fatorar o número ímpar N,
devemos encontrar x e y tais que  . A procura inicia-se com 
igual ao menor inteiro maior ou igual a  .
Essa escolha garante que  ,
condição necessária para encontrar y tal
que  .
Escolhido  ,
constrói-se, como no exemplo da página 7, a tabela:

até
encontrar um  que
seja um quadrado perfeito. que
seja um quadrado perfeito.
Mas, observe:
 e,
portanto, e,
portanto,  , ,
 e,
portanto, e,
portanto,  , ,
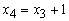 e,
portanto, e,
portanto,  . .
Prosseguindo dessa forma, teremos 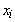 e
e  dados recursivamente
dados recursivamente
por 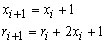
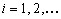
e o processo pára quando
 for
um quadrado perfeito. As igualdades acima podem ser provadas usando
indução infinita. for
um quadrado perfeito. As igualdades acima podem ser provadas usando
indução infinita.
Veja como fica agora a fatoração
já vista de  , ,
 : :

Não foi mais necessário calcular 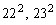 e e
 ,
pois usando a fórmula recursiva, só aparecem termos lineares
em ,
pois usando a fórmula recursiva, só aparecem termos lineares
em  e
e  . .
Fermat ilustrou seu método tomando como exemplo a fatoração
de 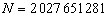 . .
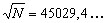 ; ;
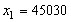
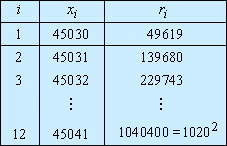
N = 450412 - 10202 = (45041 + 1020) . (45041 - 1020) = 46061 x 44021,
resultado obtido por Fermat.
A experiência de construir conceitos, e reconhecer interrelações
entre conteúdos matemáticos aparentemente desconexos,
desenvolve habilidades necessárias à aprendizagem matemática,
complementa a visão tradicional oferecida pelos livros didáticos,
e pode estimular as mentes mais curiosas a investigar o comportamento
dos números.
Referência bibliográfica
CHABERT, J.L. et al. A History of Algorithms.
Springer - Berlin, 1999.
|