|
Cláudio Possani
Élvia Mureb Sallum
Flávio Wagner
Rodrigues
IME-USP
Soluções e Sugestões
RPM - Problemas
Caixa
Postal 66281
05311-970 São Paulo, SP
|
 |
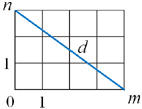
218. Dados m e n inteiros
positivos, considere um retângulo, de base m e altura n,
quadriculado
com coordenadas inteiras. Determine o número de pontos de encontro da
diagonal do retângulo, d, com o quadriculado incluindo os lados do
retângulo original.
(Proposto por José Antonio Verderesi, SP.)
219. Dados x e y números
inteiros positivos, mostre que, se x2 + y2 + xy é
divisível por 10 então é divisível por 100.
(Proposto por Luiz Fichmann,
SP.)
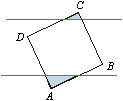 220.
Considere duas retas paralelas que distam a entre si e um quadrado
ABCD, de lado a, situado no plano das paralelas numa posição
tal que os vértices A e C estejam em lados opostos do plano dividido pela
faixa das paralelas. 220.
Considere duas retas paralelas que distam a entre si e um quadrado
ABCD, de lado a, situado no plano das paralelas numa posição
tal que os vértices A e C estejam em lados opostos do plano dividido pela
faixa das paralelas.
Calcule a
soma dos perímetros dos triângulos sombreados.
(XIV Asian Pacific Mathematics Olympiad, enviado por
Cláudio Arconcher, SP)
221. Denotando por [x] o maior
inteiro menor ou igual a x, determine para que valores de x
cada uma das igualdades abaixo é verdadeira
: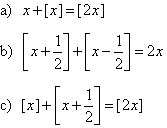
1. A média das idades dos elementos de uma
equipe de uma feira de ciências é 14,625. Qual é o menor número de
elementos que podem constituir a equipe?
(XXI Olimpíadas Portuguesas de
Matemática.)
 2. No Jardim dos Números, os algarismos
a e b passeavam a
uma velocidade constante. Às 2. No Jardim dos Números, os algarismos
a e b passeavam a
uma velocidade constante. Às
 14:00 h já tinham percorrido
ab metros, às 14:42 h
ba metros e às 15:00 h
a0b
metros. 14:00 h já tinham percorrido
ab metros, às 14:42 h
ba metros e às 15:00 h
a0b
metros.  Sabendo que no número a0b o algarismo das
dezenas é zero, mas o das Sabendo que no número a0b o algarismo das
dezenas é zero, mas o das
 centenas não, a «que horas começou o passeio? centenas não, a «que horas começou o passeio?
(XXI Olimpíadas Portuguesas de Matemática.)
3. Um destacamento de soldados precisa atravessar um rio muito profundo e
sem pontes. Eles  pedem ajuda a dois meninos que estão passando pelo rio num
barco. Porém, o barco é tão pequeno que nele só cabem os dois meninos ou
um soldado de cada vez. Como eles fizeram para todos os soldados
atravessarem o rio? pedem ajuda a dois meninos que estão passando pelo rio num
barco. Porém, o barco é tão pequeno que nele só cabem os dois meninos ou
um soldado de cada vez. Como eles fizeram para todos os soldados
atravessarem o rio?
(Do livro En el reino del ingenio, de E.I.
Ignátiev)
(Ver
respostas na
seção "O leitor pergunta")
|
Soluções dos problemas propostos na RPM 50 |
210.
Mostre que, se a, b, c são números inteiros ímpares, então a
equação ax2bx+c=0 não tem raízes racionais.
Solução
Se existe uma
raiz racional, temos b2 > 4ac e também temos que b2
 4ac
é um quadrado perfeito m2. Sendo b ímpar,
b2 é ímpar e, como 4ac é par, temos b2 4ac
é um quadrado perfeito m2. Sendo b ímpar,
b2 é ímpar e, como 4ac é par, temos b2
 4ac ímpar,
implicando m2 ímpar, que, por sua vez, implica m
ímpar. Como b2 4ac ímpar,
implicando m2 ímpar, que, por sua vez, implica m
ímpar. Como b2
 m2 = 4ac e a
diferença dos quadrados de dois números ímpares é sempre um múltiplo de 8
(verifique!), conclui-se que 4ac é múltiplo de 8. Mas, sendo a e
c ímpares, 4ac não é um múltiplo de 8; logo, a equação ax2+bx+c=0 não tem raízes racionais. m2 = 4ac e a
diferença dos quadrados de dois números ímpares é sempre um múltiplo de 8
(verifique!), conclui-se que 4ac é múltiplo de 8. Mas, sendo a e
c ímpares, 4ac não é um múltiplo de 8; logo, a equação ax2+bx+c=0 não tem raízes racionais.
211.
Numa classe com 12 alunos, o professor escreveu na lousa um número natural
menor que 50 000 e pediu que os alunos falassem alguma coisa a respeito
dele. O primeiro aluno disse que o número era múltiplo de 2, o segundo
disse que o número era múltiplo de 3 e assim sucessivamente até o último,
que disse que o número era múltiplo de 13. Em seguida o professor disse
que, com exceção de dois alunos consecutivos que erraram, todos os demais
acertaram.
a) Quais foram os alunos que
erraram?
b) Qual foi o número que o
professor escreveu? Justifique suas respostas.
Solução
Analisando os
pares de números consecutivos, 2 e 3; 3 e 4; 4 e 5; 5 e 6; 6 e 7; 9 e 10; 10 e 11;
11 e 12; 12 e 13, é fácil verificar que se dois alunos
consecutivos erraram ao afirmar que o número era múltiplo de um desses
pares, então o número de alunos que erraram seria maior que 2. Restam,
portanto, os pares 8 e 9 e 7 e 8 e o par que produz um número menor que 50 000 é o
par 7 e 8 ao qual corresponde o número 25 740.
(Adaptado de soluções enviadas por vários leitores.)
212.
Seja  uma parábola com foco F e seja PQ um segmento que contém
F, com P e, Q pertencentes a uma parábola com foco F e seja PQ um segmento que contém
F, com P e, Q pertencentes a
 . Sejam r e s as retas tangentes
a . Sejam r e s as retas tangentes
a  , respectivamente em P e
Q, e seja C o ponto de encontro de r
e s.
Obtenha a medida do ângulo PCQ e determine o lugar geométrico
de todos os pontos C obtidos. , respectivamente em P e
Q, e seja C o ponto de encontro de r
e s.
Obtenha a medida do ângulo PCQ e determine o lugar geométrico
de todos os pontos C obtidos.
Solução
Seja
 a parábola de foco F e
diretriz d. Dado um ponto P a parábola de foco F e
diretriz d. Dado um ponto P

 ,
admitiremos conhecido que a reta tangente à ,
admitiremos conhecido que a reta tangente à
 em P é bissetriz de
APF, onde AP é perpendicular à d. em P é bissetriz de
APF, onde AP é perpendicular à d.
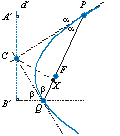
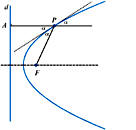 Considere P e Q dois
pontos em Considere P e Q dois
pontos em  tais que
PQ contém o foco F. Sejam
C o ponto de
encontro das tangentes a tais que
PQ contém o foco F. Sejam
C o ponto de
encontro das tangentes a  em P e Q, d' a reta paralela à d
por C, PA' e
QB' perpendicular a
d' e CX perpendicular a
PQ.
Pela congruência dos triângulos CXP e CB'Q, concluímos
que em P e Q, d' a reta paralela à d
por C, PA' e
QB' perpendicular a
d' e CX perpendicular a
PQ.
Pela congruência dos triângulos CXP e CB'Q, concluímos
que  + +
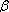 = 90°. Assim P = 90°. Assim P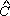 Q é um ângulo reto. Queremos mostrar agora
que C Q é um ângulo reto. Queremos mostrar agora
que C  d. d.
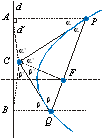
Na figura à direita, temos
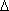 ACP ACP

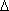 FCP (caso LAL) e FCP (caso LAL) e
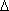 BQC BQC

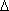 FQC (caso LAL). Assim, ACB =
2 FQC (caso LAL). Assim, ACB =
2 ' + 2 ' + 2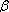 '
= 2 . 90° = 180° isto é, C pertence à diretriz d. '
= 2 . 90° = 180° isto é, C pertence à diretriz d.
(Solução
adaptada das soluções enviadas por diversos leitores.)
213.
Em um triângulo acutângulo ABC, sejam P e Q os pés das
alturas relativas aos lados AB e AC respectivamente, M o
ponto médio de BC e D a intersecção de CP e BQ. Prove que:
a) a circunferência
 determinada por APQ passa por D.
determinada por APQ passa por D.
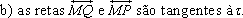
c) as circunferências determinadas por
CQM, BPM e  possuem um ponto comum.
possuem um ponto comum.
Solução
a) Como
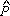 + +
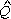 =180°, o quadrilátero
APQD é inscritível; logo, a circunferência determinada por APQ
passa por D. =180°, o quadrilátero
APQD é inscritível; logo, a circunferência determinada por APQ
passa por D.
b) O
triângulo POA é isósceles e, se
 é a medida de seus ângulos
internos congruentes, temos, no triângulo ABH, é a medida de seus ângulos
internos congruentes, temos, no triângulo ABH,
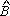 = 90° = 90°

 e, no
triângulo PCM, temos o ângulo M e, no
triângulo PCM, temos o ângulo M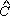 P ou B P ou B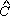 P com
medida
igual a P com
medida
igual a  . O triângulo PCM é isósceles;
logo, também é . O triângulo PCM é isósceles;
logo, também é
 a medida
do ângulo C a medida
do ângulo C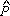 M.
Daí segue que a medida de O M.
Daí segue que a medida de O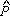 D é
90° D é
90° 
 , e, portanto, a medida de
O , e, portanto, a medida de
O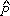 M = 90° M = 90°

 + +
 = 90°, o que implica que MP é tangente a = 90°, o que implica que MP é tangente a
 . Analogamente para MQ. . Analogamente para MQ.
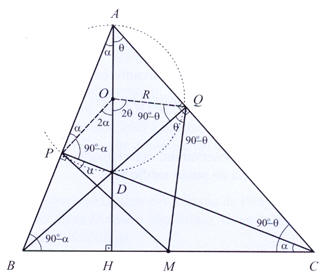
c) Seja K o segundo ponto de encontro de
 com a circunferência determinada por
Q, M e C. Os
quadriláteros MKQC e APKQ são inscritíveis; logo, medida M com a circunferência determinada por
Q, M e C. Os
quadriláteros MKQC e APKQ são inscritíveis; logo, medida M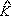 Q =
180° Q =
180°
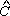 e, medida P
e, medida P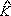 Q = 180° Q = 180°

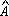 , o que implica medida P , o que implica medida P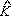 M = M =
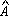 + +
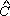 e, como
e, como
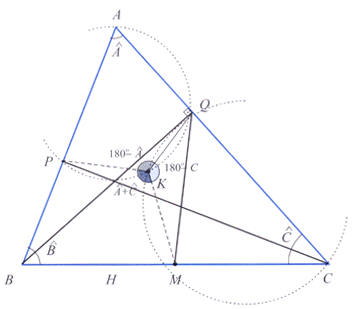
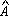 + +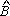 + +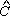 =180°,
segue que BPKM é inscritível e, assim, a circunferência determinada
por B, P e M também passa por K. =180°,
segue que BPKM é inscritível e, assim, a circunferência determinada
por B, P e M também passa por K.
Concluímos, então, que as
três circunferências concorrem em K.
(Solução adaptada das soluções enviadas por João F. de
Moura e José Cláudio M. Veloso.)
Obs.:
Alguns leitores observaram, corretamente, que o item c) pode ser provado
sem referência ao ponto médio M.
|
Relação dos
leitores que enviaram soluções dos problemas da RPM 50 |
|
Alan Henrique de Sá, RJ: 210, 211 |
João F. Moura, RJ: 210, 211, 212, 213 |
|
Amadeu C. Almeida, RJ: 211, 213 |
João Linneu
A. Prado, SP: 210, 211, 213 |
|
Amaro José de O. Filho, PE: 210,
211 |
Joaquim Ferreira da Silva, PE: 211 |
|
Aníbio
Pacheco, SC: 210, 211 |
José C. M. Veloso, RJ: 210, 211, 212, 213 |
|
Antonio
Ferreira Sobrinho, SP: 211 |
Luiz César Niehues,
SC: 211 |
|
Antonio
Luiz Miranda, RJ: 211 |
Mauro Felix de Sousa, RJ: 210 |
|
Antonio
M. Santos, PR: 210, 211,212,213 |
Rizio SantAna,
MG: 210, 211 |
|
Celso Martinez Rodrigues, MG: 211 |
Roberto Alexandre Loewenberg,
SP: 211 |
|
Clodoaldo Lessa, SP: 210 |
Roberto P. Chagas, MG: 210, 211, 212 |
|
Eduardo Luís Estrada, SP: 210 |
Sebastião Maurício Santos, MG: 210, 211 |
|
Érico Rodrigues Silva, MG: 211 |
Sérgio S. Correia Jr., RJ: 210,
211, 212 |
|
Fernando Carvalho Ramos, RS: 211 |
Tsunediro Takahashi, SP- 211 |
|
Flávio Ricardo L. da Cunha, GO: 211 |
Victor Chakur.SP-210,211 |
|
Florival
Carlos Souza, GO: 210, 211 |
Wanderley
Gambá, SP- 211, 212 |
|
Geraldo Cláudio Broetto,
ES: 210 |
Robério
L. de Carvalho, CE - 210, 211 |
|
Geraldo Perlino
Jr., SP: 211, 212, 213 |
Paulo Sérgio C. Lino.MG-212 |
|
Henrique O. Pires, MG: 210, 211, 212 |
Milton Dini Maciel, SP - 210, 211, 212 |
|
Jaime Oliveira, SE: 211, 212 |
Carl Henning Schinke, RJ |
|