João Pitombeira de Carvalho
Departamento de Matemática, PUC-Rio

Suponhamos que você tem uma calculdadora de bolso que efetua as quatro operações, e extrai raízes quadradas. Será possível, usando essa calculadora, extrair a raiz n-ésima de um número qualquer?

No artigo Vamos usar a calculadora publicado na RPM 26, p. 16 os autores mostram como calcular a raiz cúbica de um número e também como calcular . Na verdade, dado um número real x, não negativo, usando somente as teclas é possível achar , onde p e q são números naturais. Vamos explicar como isso é possível:

Exemplo: Calcule .

Seja Então, e vemos que donde Vamos construir uma sequência como na tabela, usando uma calculadora para obter os números da segunda coluna:





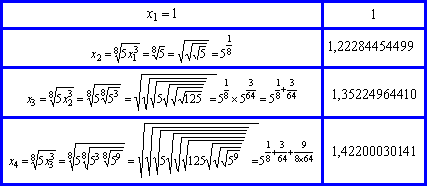
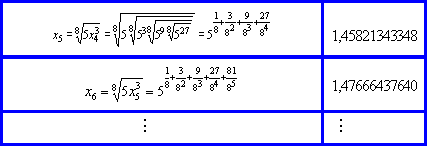
De maneira geral, e, vemos que para calcular , conhecendo , é suficiente utilizar as teclas de raiz quadrada (pois ) e de produto (para elevar ao cubo e em seguida multiplicar o resultado por 5).

Aceitando que a sucessão converge para o limite x, e que esse limite é diferente de 0, podemos fazer:

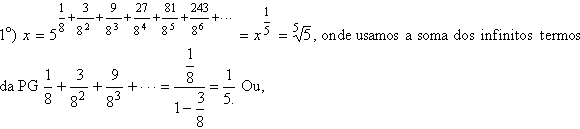
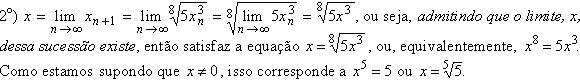Toda a argumentação anterior foi baseada no fato de que a sucessão converge. Isso realmente acontece? Para responder a essa pergunta faremos uma pequena digressão: Os gráficos das funções e estão mostrados na figura a seguir e como o número procurado, satisfaz vemos que x será exatamente a abscissa, com , do ponto de intersecção dos gráficos de e .

Ora, o fato algébrico de que a raiz existe, é equivalente ao fato de que os gráficos se cortam. Para o gráfico de estará acima do gráfico de .

Partindo de um valor arbitrário, por exemplo, , examinemos a seguinte sucessão de pontos do plano cartesiano, representados no gráfico acima:

Observe que os pontos estão sobre o gráfico de e que os pontos estão sobre o gráfico de .

Os pontos convergem para o ponto , que é exatamente o ponto de intersecção dos dois gráficos. É então óbvio que a sucessão converge exatamente para . Pode-se mostrar, rigorosamente, usando, por exemplo, as técnicas expostas em [1], que isso realmente acontece.

Quanto a escolha, ela foi feita simplesmente para facilitar os cálculos e também por sabermos que está próximo de 1. Se tivéssemos escolhido qualquer outro valor para , por exemplo, o limite da sucessão, que estamos supondo existir, continuaria satisfazendo
Você certamente já percebeu o procedimento geral: se quisermos calcular ou seja, achar x tal que devemos transformar essa igualdade de modo a obter, do lado esquerdo, um expoente que seja uma potência de 2. Isso é feito multiplicando-se os dois membros por uma potência conveniente de x. Assim, por exemplo, se então donde ou e utilizaremos a sucessão na qual

 

Quadrados mágicos e o teorema de Pitágoras
	A constante mágica do quadrado construído sobre o cateto maior é igual a 46, a constante do quadrado sobre o cateto menor é 147 e a constante do quadrado sobre a hipotenusa é igual a 125. Consequentemente, a soma de todos os números dos quadrados citados é, respectivamente, 184, 441 e 625. Assim, a soma dos números do quadrado construído sobre a hipotenusa, 625, é igual a soma dos números dos quadrados construídos sobre os catetos, 184 + 441.
Enviado por Bruno Alves da Silva, Rio de Janeiro, que se baseou em texto publicado por Elisha Scott Loomis, publicado pelo National Council of Teacher of Mathematics, de 1972.