Cláudio Possani
Élvia Mureb
Sallum
Flávio Wagner Rodrigues
IME–USP
Soluções e Sugestões
RPM – Problemas
Caixa Postal 66281
05311-970 São Paulo, SP
|

|
206.
Suponha que cada ponto de um plano seja pintado de uma cor escolhida
entre três cores dadas. Prove que existem dois pontos de mesma cor cuja
distância é k, sendo  um número real dado.
um número real dado.
207.
Um rapaz esqueceu o último algarismo do telefone da namorada e
resolveu tentar falar com ela escolhendo ao acaso o último dígito. Se ele está
num telefone público e só tem duas fichas, qual é a probabilidade de que ele
consiga conversar com a namorada?
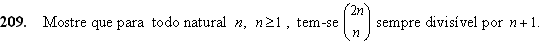
3.
Obtenha a palavra MU começando com a
palavra MI e por uma seqüências de aplicações das seguintes regras:
a)
toda palavra pode ser triplicada.
b)
uma letra U pode ser substituída por duas letras I seguidas (II).
c)
quatro letras I seguidas podem ser eliminadas.
d)
depois de uma letra M pode ser colocada uma letra U.
e)
se em uma palavra aparece IMU podemos eliminar a letra M.
|
2.
Calcule, sem usar calculadora, a área sombreada sendo
 e e

|

|
1.
 Em
homenagem ao “PENTA” vamos pintar os lados de um pentágono regular com as duas
cores verde e amarelo. De quantas maneiras diferentes podemos fazer isso? Em
homenagem ao “PENTA” vamos pintar os lados de um pentágono regular com as duas
cores verde e amarelo. De quantas maneiras diferentes podemos fazer isso?
 Considera-se
que duas pinturas são iguais quando é possível obter uma a partir da outra
através de um movimento rígido no plano. Considera-se
que duas pinturas são iguais quando é possível obter uma a partir da outra
através de um movimento rígido no plano.
(Ver
respostas na
seção "O leitor pergunta")
|
Soluções dos problemas propostos na RPM 47 |
198.
Para cada número natural, n, n
 0,determinar
os inteiros a, b, c e d, 0,determinar
os inteiros a, b, c e d,
 , tais que , tais que
 . .
Solução:
Sejam a, b, c,
d inteiros,  , com , com
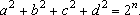
Para
 a única possibilidade
é a única possibilidade
é  e para e para
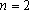 temos duas
possibilidades temos duas
possibilidades  e e
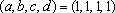 . .
Consideremos
 . .
Quanto a paridade dos números a,
b, c e d, pode acontecer: todos são pares, todos são
ímpares ou dois deles são pares e dois ímpares.
Não podemos ter todos ímpares pois:
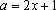 , ,
 , ,
 e e
 implica implica
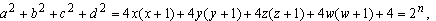 ou, ou,
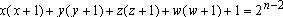 , o que é impossível,
uma vez que , o que é impossível,
uma vez que 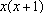 , ,
 , ,
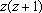 e e
 são todos pares. são todos pares.
Também não podemos ter dois pares e dois
ímpares pois:
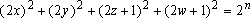 implica implica
 , de novo, uma igualdade
impossível. , de novo, uma igualdade
impossível.
Assim, para
 , devemos ter os
números a, b, c e d todos pares: , devemos ter os
números a, b, c e d todos pares:
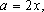  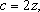
 Logo, Logo,
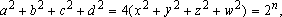 ou ou

Repetindo o processo, agora para os
números x, y, z e w, obtemos:

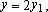 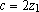 e
e  , ou , ou
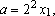 
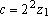 e e
 , com , com

Se n é ímpar,
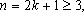 repetindo o processo
anterior k vezes, podemos escrever repetindo o processo
anterior k vezes, podemos escrever

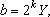 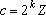 e
e  com com
 donde donde
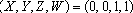 e e
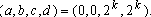
Se n é par,
 repetindo o processo repetindo o processo
 vezes, temos vezes, temos

 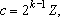
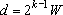 com com
 , donde , donde
 ou ou
 e e
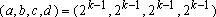 ou ou
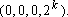
(Solução adaptada da enviada por Carlos
Alberto da Silva Victor, RJ.)
|
|
|
|
199.
Considere ABC um triângulo de área 5.
Para cada ponto
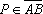 , mais próximo de
A do que de B, considere , mais próximo de
A do que de B, considere
 e e
 de modo que de modo que
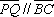 , ,
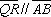 e e
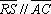 . Determine o valor
máximo atingido pela área do quadrilátero PQRS. . Determine o valor
máximo atingido pela área do quadrilátero PQRS.
|

|
Solução:
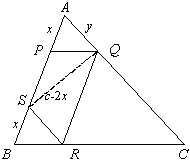 |
De QR = PB = AS, temos, AP
= SB = x.
Se AB = c, BC = a e
AC = b, da semelhança dos
  de SPQR é dada por
de SPQR é dada por
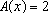 área
área  AQS – área APQ,
AQS – área APQ,
|
 (Solução
de Milton Dini Maciel, SP.)
(Solução
de Milton Dini Maciel, SP.)
200.
Seja f: IN
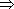 Z uma função
tal que Z uma função
tal que
i)
 se se
 , ,
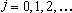 . .
ii)
 se se
 , ,
 . .
Demonstre que, para qualquer
 IN, existe
IN, existe
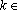 Z, Z,
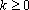 tal que tal que
 . Calcule . Calcule
 . .
Solução:
Para qualquer
 IN, existe
IN, existe
 Z, Z,
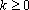 tal que tal que
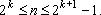
Se n = 2k+1
 1, então por
i) temos f(n) = 0 e, neste caso, f(n) + n
= 2k+1 1, então por
i) temos f(n) = 0 e, neste caso, f(n) + n
= 2k+1
 1 . 1 .
Se 2k
 n
< 2k+1 n
< 2k+1
 1 fazemos: 1 fazemos:
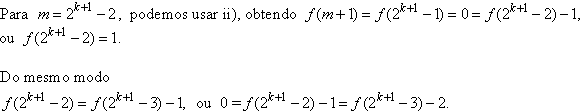

Do último termo, observando que 2k+1
 2k
= 2k , temos f(2k)
= 2k 2k
= 2k , temos f(2k)
= 2k
 1 ,
de onde f(21990) = 21990 1 ,
de onde f(21990) = 21990
 1. 1.
Para cada n, 2k
 n < 2k+1
n < 2k+1 1 temos n = 2k+1
1 temos n = 2k+1
 r ,
com 1 < r r ,
com 1 < r
 2k
logo, f(n) = r 2k
logo, f(n) = r
 1 = 2k+1 1 = 2k+1
 n n
 1, o que
prova f(n) + n = 2k+1 1, o que
prova f(n) + n = 2k+1
 1 . 1 .
|
201.
Sobre os lados de um triângulo ABC são construídos
quadrados e, em seguida, ligam-se os vértices, formando-se um hexágono
DEFGHI. Sendo
 , e , e
 , determine a área
desse hexágono. , determine a área
desse hexágono.
|

|
Solução:
O hexágono decompõe-se em sete polígonos,
sendo quatro triângulos e três quadrados.
As áreas dos quadrados são 169, 196 e
225.
Por outro lado, temos: med =
=  med med , o que implica sen
, o que implica sen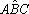 =
sen =
sen e, então, e, então,
2(área
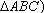 =
AB.BC.sen =
AB.BC.sen = EB.BF.sen
= EB.BF.sen
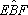 =
2(área =
2(área 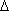 EBF)
. Logo, área EBF)
. Logo, área
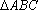 = área = área

De modo análogo mostra-se que as áreas dos
quatro triângulos são iguais.
Usando a fórmula de Heron para calcular a
área 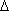 ABC
obtemos ABC
obtemos  Assim, a área do hexágono é igual a 926.
Assim, a área do hexágono é igual a 926.
|
Relação dos leitores que
enviaram soluções
dos problemas da RPM 47 |
Ademir Sartim, ES – 199, 201
|
Jorge David Jr., SP – 201
|
|
Alberto Hassan Raad, MG –
199, 201
|
José Evandro Lemes, RJ – 199, 201
|
Alixanzito R. S. Costa, CE – 201
|
José Hernandes, SP – 201
|
Amadeu C. de Almeida, RJ – 199, 200, 201
|
Luiz César Niehues, SC –
201
|
|
Amaro José de Oliveira Fo,
PE – 199, 201
|
Luiz H. Ribeiro dos Santos, PR – 201
|
Antonio Ferreira Sobrinho, SP – 201
|
Milton Dini Maciel, SP –
199, 201
|
|
|
Paulo Roberto Mendonça, SP – 201
|
Carl Henning Schinke, RJ –
201
|
Paulo Sérgio C. Lino, MG – 199
|
Carlos A. S. Victor, RJ –
198, 199, 201
|
Pierre Bedouch, MG – 199
|
Carlos Alexandre Gomes, RN – 201
|
Roberto Luís Dotto, SP – 201
|
Cristovom A. Girodo, SP – 201
|
Roberto Pinheiro Chagas, MG – 199
|
Fernanda Teles Nunes, MG – 201
|
Ronaldo A. dos Santos, GO – 199, 201
|
Fernando Carvalho Ramos, RS – 201
|
Ruy Carlos Miritz, RS –
201
|
Francisco Rocha F. Neto, MA – 201
|
Sebastião M. dos Santos, MG – 199, 201
|
Geraldo Perlino Jr., SP – 199, 201
|
Tsunediro Takahashi, SP – 201
|
Geraldo Perlino, SP – 201
|
Vander L. Martins, RJ – 201
|
Guita Nascimento, RJ – 201
|
Victor Chakur, SP – 199,
201
|
Jaime Oliveira, SE – 199
|
Wanderley Gamba, SP – 199,
201
|
João Ferreira, AP – 201
|
Zilton Gonçalves, RJ – 199,
201
|
|