Gilson Braviano
M^a Helena W. L. Rodrigues

Há alguns anos um novo termo vem sendo usado na área da Matemática e da Educação Matemática: Geometria Dinâmica. Não se trata de uma nova Geometria, ou uma alternativa à Geometria Euclidiana, como aquela de Lobachevski, mas simplesmente uma exploração da idéia de movimento para descrições geométricas.

Parece-nos interessante que professores de Matemática conheçam melhor o significado da chamada Geometria Dinâmica e se ela pode ser-lhes útil. Este é o objetivo desse artigo: pôr os leitores da RPM a par dessa nova expressão e dar informações que permitam a cada um decidir se vale a pena embrenhar-se nessa trilha.
 

A idéia de movimento na Geometria não é recente; os geômetras gregos idealizaram vários instrumentos para descrever curvas mecanicamente definidas. Porém, o uso de movimento entre eles era evitado por uma questão de purismo lógico. O século XVII marcou uma quebra com a tradição grega e o uso do movimento para estabelecer propriedades geométricas ou realizar construções geométricas tornou-se explícito. [Colette Laborde (apud Scher 2000)] .

Foi, no entanto, em meados da penúltima década do século XX¹ que nasceu um instrumento que permite a abordagem da Geometria de modo efetivamente dinâmico, usando o  computador. Trata-se  da  possibilidade de fazer construções eletrônicas como aquelas com régua e compasso e outras mais. Além disso, elementos básicos podem ser manipulados através do teclado ou do mouse, deslocando-se na tela e trazendo atrelados a si os elementos construídos a partir deles, ou seja, não alterando a posição relativa entre eles. Nessa mudança automática de posição está o dinamismo, cuja grande vantagem é preservar relações entre os elementos da figura. Assim, por exemplo, se uma reta  r  foi inicialmente construída de modo a ser a mediatriz de um segmento  AB,  é possível impor que, ao mudarmos a posição de um dos extremos  A  ou  B,  ela se desloque automaticamente, mantendo-se como mediatriz do novo segmento.

O importante é que essa característica permite explorar diversas instâncias de um problema em busca da verificação de uma conjectura. E isso pode ser feito desde cedo por qualquer estudante.

No decorrer deste artigo apresentaremos sucintamente três dos softwares que nos permitem trabalhar com a Geometria Dinâmica.

O termo “Dynamic Geometry” é, na verdade, marca registrada da Key Curriculum Press, responsável pela comercialização do Geometer’s Sketchpad, um dos programas de Geometria Dinâmica que será mencionado na seqüência deste artigo.  

Sant (1995, pág. 36), em artigo publicado no número 29 da RPM sob o título O Cabri-Géomètre, descreve o software como sendo “um programa de computação que traça figuras geométricas, permite sua deformação mantendo algumas características da figura de partida e mede segmentos e ângulos.”

O CABRI, ao contrário de muitos programas, é voltado para o uso em sala de aula com o objetivo de facilitar a aprendizagem, funcionando como um caderno de rascunho interativo (em francês: CAhier de BRouillon Intéractif) e informatizado. Sua potencialidade para tratar problemas geométricos (até então resolvidos graficamente com régua e compasso) permite que seja utilizado a partir dos últimos anos do curso Fundamental, dando oportunidade aos professores de verificar o conhecimento dos alunos com relação a questões de Geometria ou a problemas que dificilmente poderiam ser abordados somente com o uso de lápis, papel e instrumentos de desenho. 

O Cabri-Géomètre II é dotado de novos recursos (como a construção de certos lugares geométricos, de cônicas por 5 pontos, a associação de elementos de Geometria Analítica às construções, a ilustração de características dinâmicas através de animações, entre outros) e parece ser o software de Geometria Dinâmica mais utilizado no Brasil. Existem, inclusive, vários sites sugerindo atividades que podem ser realizadas em sala com ele² e dois congressos³ internacionais já foram realizados exclusivamente para divulgar suas potencialidades, o primeiro deles ocorrido no Brasil.

Citamos, a seguir, outros programas de Geometria Dinâmica bem conhecidos:

    The Geometer’s Sketchpad: tem funcionalidades muito próximas àquelas do Cabri, porém com um menu de opções propositalmente reduzido. Outra diferença é que os elementos devem ser escolhidos antes de selecionar-se a construção a ser realizada. Na home page da Key Curriculum Press (http://www.keypress.com) pode ser obtida uma versão demonstração gratuita do Geometer’s Sketchpad.

   Cinderella: diferentemente dos programas acima citados, este software, como destaca Burgiel (1999), foi exclusivamente desenvolvido por e para pesquisadores matemáticos, permitindo o trabalho com as Geometrias euclidiana, hiperbólica e elíptica. Criado na Alemanha, e lançado comercialmente em 1999, pode ser executado em qualquer plataforma. A versão demonstração gratuita deste programa pode ser obtida através do site http://www.cinderella.de.

Pesquisadores e educadores estão se empenhando em explorar as potencialidades dos programas de Geometria Dinâmica. No Brasil, particularmente, alguns resultados podem ser vistos nos trabalhos publicados em eventos científicos. Apenas como exemplo, cita-se que no VII ENEM⁴ (Encontro Nacional de Educação Matemática), realizado no Rio de Janeiro em julho de 2001, foram apresentados mais de dez trabalhos nesse contexto.

No GRAPHICA´2001⁵ uma das sessões técnicas e um workshop dedicaram-se completamente a este tema, inclusive, apresentando à  comunidade da área gráfica programas que implementam a Geometria Dinâmica, desenvolvidos por equipes de pesquisadores brasileiros⁶.  

Não é por acaso que existe tanto interesse em melhorar o ensino da Geometria. Em 1988, José Carlos Putnoki publicou na RPM 13 uma matéria intitulada Que se Devolvam a Euclides a Régua e o Compasso, de onde extraímos o seguinte texto:

“Já faz um bom tempo que o Desenho Geométrico foi banido das nossas escolas de primeiro e segundo graus. Coincidentemente, de lá para cá, a Geometria, cada vez mais, vem se tornando o grande terror da Matemática, tanto para alunos quanto para professores. Com certeza, não se trata apenas de uma coincidência, mas sim, em parte, de uma conseqüência.”

Ora, sendo esta disciplina formativa, portanto imprescindível na formação de profissionais que lidam com a Geometria e com as relações espaço/forma, não se estranha que o mercado de trabalho acabe deparando-se com profissionais que não distinguem formas, que não diferenciam sequer, nas representações bidimensionais, formas planas e objetos que possuem volume. 

A escola não pode funcionar mais como um meio inibidor do desenvolvimento das noções espaciais do estudante. Com o advento do computador e sua inserção nas escolas, ainda que por etapas, pode-se oferecer aos alunos a possibilidade de aprimorar seus conhecimentos geométricos usando ambientes computacionais que executem a Geometria Dinâmica.

Não querendo ser exaustivos na apresentação deste tema, lembramos que uma das contribuições do uso da Geometria Dinâmica no ensino vem da possibilidade de tornar disponíveis representações gráficas de objetos geométricos que aproximam o objeto material da tela do computador (desenho) do objeto teórico (figura). Ela favorece o desenvolvimento de uma leitura geométrica do desenho para o aprendiz, contornando, assim, uma das dificuldades do ensino da Geometria (o desenho é, em geral, o objeto de raciocínio do aluno, enquanto o professor aborda a figura).

Esses programas merecem, portanto, ser explorados e avaliados por nós, profissionais na área da educação.  
 

Assim, a Geometria Dinâmica não é uma nova Geometria pois não se baseia em outros axiomas ou proposições nem em novas relações de espaço-forma, mas sim um termo usado para designar um modo dinâmico e interativo de trabalhar a Geometria e suas propriedades usando editores gráficos construídos para esse fim. 

Há que se lembrar também que qualquer desenho no computador é construído a partir de um número finito de pontos e, por menos que se perceba, a dinâmica também se dá discretamente, isto é, as várias posições, embora muito próximas, são em número finito também. A grande diferença é que estas posições são desenhadas numa grande velocidade, o que nos permite obter um número muito grande delas.

Ao considerar o emprego de computadores na educação como um meio que possibilita a aprendizagem ativa, cabe a você, professor de Matemática, decidir se é o momento de integrar essa ferramenta em suas aulas (em particular, aquelas de Geometria e desenho geométrico). Este artigo fornece um ponto de partida (e por que não dizer... incentivo?) para que você possa avaliar mais concretamente essa possibilidade.

__________

1 Mais precisamente, em 1985, na cidade de Grenoble (França), nasceu o Cabri-Géomètre e, ao mesmo tempo,  nos Estados Unidos, o Visual Geometry Project começava o desenvolvimento de uma ferramenta computacional para realizar desenhos de maneira precisa usando régua e compasso eletrônicos, a qual, mais tarde, se chamaria The Geometer’s Sketchpad.  

2 Como exemplo, citamos: http://www.cabri.com.br e http://www.mat.ufrgs.br/~edumatec.

3  Em http://www.cabri.com.br pode ser obtido material referente ao Cabri World I, realizado em 1999, na cidade de São Paulo. Estão à disposição em  http://www.cabriworld.net informações relativas ao segundo congresso, realizado no Canadá em 2001.

4  Ver http://www.viienem.ufrj.br.

5  15^o Simpósio Nacional de Geometria Descritiva e Desenho Técnico & IV International Conference on Graphics Engeneering for Arts and Design, realizado em novembro de 2001, cuja home page é:  http://www.pcc.usp.br/graphica2001

6  Os programas em questão são: Transpontuais (ambiente computacional didático desenvolvido por Maria Helena Wyllie Lacerda Rodrigues e Daniel Wyllie Lacerda Rodrigues) e Tabulae (desenvolvido por Luiz Carlos Guimarães).
____________

Referências bibliograficas

[1]   BELLEMAIN, F. Geometria Dinâmica: Diferentes implementações, papel da manipulação direta e usos na aprendizagem. In: CD Rom do GRAPHICA (15^o Simpósio Nacional de Geometria Descritiva e Desenho Técnico & IV International Conference on Graphics Engeneering for Arts and Design). São Paulo, 2001.

[2]   BURGIEL, H. Rewiew of the interactive geometry software Cinderella. Mathematical Association of America, 1999.

[3]   PUTNOKI, J.C. Que se devolvam a Euclides a régua e o compasso. RPM 13, p. 13-17.

[4]   SANT, Jean-Marc. O “Cabri Geomètre”, RPM 29 (1995), pg 36-40.

[5]   SANTOS, E. T. Novas tecnologias no ensino de desenho e Geometria. In: I Encontro Regional do Vale do Paraíba de Profissionais de Ensino na Área de Expressão Gráfica; p. 71-81; Outubro, 2000.

[6]   SCHER, D. Lifting the Curtain: The evolution of the Geometer’s Sketchpad. In: Mathematics Educator, vol. 10, n^o 2, p. 42-48, 2000.

Leônidas de Oliveira Brandão
Depto. de Ciência da Computação, IME – USP
leo@ime.usp.br

Neste artigo apresentaremos um exemplo de atividade que utilizamos para estudos de geometria, algoritmos e progressões geométricas (PG) a partir de fractais; e fractais construídos por algoritmos geométricos. Essa atividade pode ser utilizada, sob diferentes pontos de vista, no ensino médio e no primeiro ano de graduação em exatas. Com essa atividade desejamos mostrar como o computador pode catalisar o processo de aprendizagem, principalmente num ensino que privilegie o pensar, construir, testar... Outro objetivo deste artigo é ilustrar como é possível, com programas de Geometria Dinâmica (GD), estudar o conceito de algoritmo. Vale destacar que disponibilizamos no endereço http://www.matematica.br/igeom um programa gratuito de GD com o qual o professor pode desenvolver as propostas aqui apresentadas.  
 

O uso do computador pode trazer grandes benefícios ao ensino de matemática, mas para isso é necessário escolher programas (software) adequados e uma metodologia que tire proveito das características do computador, como boas representações gráficas e rapidez em cálculos.

Um bom exemplo dessa agilização no estudo de Matemática é o uso (adequado) de programas de Geometria Dinâmica (GD) [5]. Podemos dizer que a GD é a implementação, no computador, de construções com régua e compasso, na qual o estudante pode, a partir de uma construção inicial, mover com o mouse algum dos objetos iniciais. O programa se encarrega de redesenhar toda sua construção, de modo aparentemente contínuo.

Dessa forma, um programa de GD possibilita ao aprendiz, a partir de uma única construção, efetuar um número arbitrário de testes (para procurar ou verificar uma conjectura), o que seria praticamente impossível com régua e compasso. Por isso podemos dizer que a GD é do tipo 1-construção, n-testes, enquanto a geometria de “régua e compasso” é do tipo 1-construção, 1-teste.

Um exemplo simples pode ilustrar o dinamismo desse processo: a construção da mediatriz de dois pontos dados, A e B. Para construir a mediatriz basta encontrar dois pontos distintos que equidistem de  A  e  B:

Exemplo 1  Dados dois pontos, A e B, construir sua mediatriz (lugar geométrico dos pontos que equidistam dos dois pontos dados).

Construção 1  Dados: ponto A, ponto B  (resposta: construir mediatriz r).

Neste artigo não mostraremos detalhes das construções nesse ou naquele programa de GD e por isso usaremos uma linguagem simbólica para descrevê-las.

Os métodos de construção variam de programa para programa. Entretanto, todos eles dispõem de recursos que desempenham o papel da régua e do compasso. Além disso, todos eles apresentam o “dinamismo” mencionado: uma vez pronta uma construção, podemos arrastar o ponto A (ou B) pela área de desenho e o programa, automaticamente, redesenha toda a figura preservando as propriedades determinadas pela construção.

Outra característica interessante de programas de GD é introduzir a necessidade de formalização rigorosa (uma vez que o computador não admite ambiguidades) e, devido ao dinamismo, facilitar a verificação da correção das construções.

Existem vários programas de GD, que funcionam em diferentes plataformas (Linux, Windows, Mac), com licenças gratuitas ou comerciais e que exportam ou não construções para World Wide Web (ou apenas Web ou WWW).

Hoje também existem “programas nacionais” para GD, que visam atingir um número maior de usuários no Brasil, implementando recursos deixados de lado pelos programas mais conhecidos ou que sejam mais “baratos” e possam ser usados em larga escala. Temos o iGeom - Geometria Interativa na Internet, que vem sendo desenvolvido por nós (http://www.matematica.br/igeom), e que além de gratuito permite que o aprendiz/“internauta” realize suas próprias construções diretamente na Internet. Existe também o Tabullae, desenvolvido por um grupo do IM - UFRJ, coordenado por Luiz Carlos Guimarães. Ambos estão começando a ser divulgados nesse primeiro semestre de 2002.  

Uma vez que na GD as construções precisam ser bem definidas e sem ambiguidades, podemos agrupá-las na forma de função. Para isso é necessário explicitar quais (e de que tipo) são os parâmetros de entrada e de saída da função. Por exemplo, a construção da mediatriz tem como entrada os objetos geométricos “ponto, ponto” e como saída “reta”. Assim, podemos agrupá-la como a função mediatriz  sendo  e  rótulos para pontos, e depois aplicá-la em quaisquer pares de pontos, obtendo a correspondente mediatriz. No exemplo anterior a chamada da função seria mediatriz  A esse agrupamento de comandos damos o nome de macro-construções (ou apenas macro ou ainda script). Na construção da mediatriz a ordem dos pontos iniciais pode ser invertida sem qualquer alteração do resultado final. Entretanto, existem casos em que essa ordem é relevante. Um exemplo corriqueiro, em que a ordem é essencial, é a divisão de um número por outro. Abaixo apresentamos um exemplo geométrico em que ordem diferente produz resultado diferente. 

Exemplo 2. Dados os pontos  A  e  B, construir o ponto  F,  pertencente a semireta definida por  A  e  B,  tal que a distância entre  B  e  F  seja metade da distância entre  A  e  B,     

Construção 2  (dist_metade) Entrada:  ponto A,  ponto B 

Saída: ponto F, pertencente a semireta com origem em A e contendo B , e  d(B,F) = d(A,B)/2.

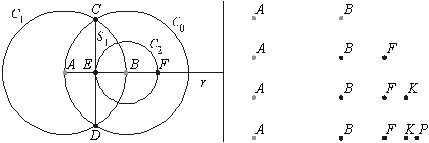
Construção do exemplo 2 (várias aplicações da macro-contrução)

Se a macro anterior for agora aplicada invertendo-se as entradas, dist_metade mantendo os pontos  A  e  B  como na figura, o ponto F ficará à esquerda de  A  e não à direita de  B.  Isso porque os conceitos de “superior”, “inferior”, “direito” ou “esquerdo” dependem de direção, no exemplo definido pela semi-reta 

Na figura acima, à esquerda, estão representados todos os objetos geométricos da construção 2. À direita, estão seguidas aplicações da macro: dist_metade depois dist_metade e então dist_metade (Alguns dos programas que dispõem de agrupamento na forma de macro são o Cabri e  GSP, ambos comerciais, e o    Dr. Genius e iGeom, gratuitos.) 

Nos exemplos anteriores, as macro-construções 1 e 2 são exemplos de algoritmos. Em cada caso existe uma sequência de entradas (em ambos, os pontos iniciais,  A  e  B),  uma sequência de passos e uma sequência de saídas (no exemplo 1 é a reta mediatriz e no 2 o ponto  F).

O exemplo 2 pode ser reescrito na forma mais compacta,

dist_metade:                      ponto x ponto  ponto

dist_metade :   e  

e pode ser utilizado para simular um problema clássico da Matemática, que leva ao paradoxo de Zenão. Esse paradoxo está apresentado e discutido na RPM 39 ([2]), sendo originado pelo exemplo a seguir.

Exemplo 3  Aquiles e uma tartaruga apostam uma corrida, sendo que Aquiles tem o dobro da velocidade da tartaruga, e por isso, a tartaruga larga à frente. Aquiles alcançará a tartaruga?

Considerando o instante inicial, , e os instantes  em que Aquiles chega à posição anteriormente ocupada pela tartaruga, a construção 2 serve para gerar os pontos  que a tartaruga ocupará quando Aquiles atingir a última posição ocupada pela tartaruga (no instante ).

Sendo A e B  as posições inciais, respectivamente, de Aquiles e da tartaruga, então:    e,

1.  Aquiles na posição : tartaruga em  dist_metade

2.  Aquiles na posição : tartaruga em dist_metade e assim por diante.

 

O uso de recorrência em macros permite escrever algoritmos, de forma elegante, para construções de fractais geométricos [3] com os quais podemos explorar conceitos de progressões geométricas, somatórios e até de convergência. O exemplo 3 pode ser utilizado para iniciar tal atividade, que deve ser seguida de exemplos graficamente mais interessantes, como o fractal baseado em circunferências, descrito a seguir.

Exemplo 4  Dados dois pontos  A  e  B  e uma circunferência    com centro  A  e passando por  B,  construir quatro novas circunferências centradas nos “polos” de    e com raio metade da primeira.

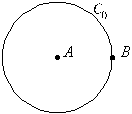
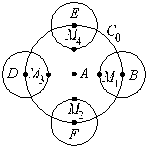
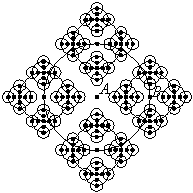
Nas figuras anteriores podemos observar três fases da construção do fractal: na primeira, a circunferência inicial tem raio  r,  na segunda está a base da macro, na terceira uma aplicação da macro com duas recorrências ( circunferências de raio  r/2²) e na última com três recorrências ( circunferências de raio  r/2³ ).

Uma possível utilização dessas figuras, no ensino médio, é trabalhar as macros como caixas pretas, sem explorar como elas foram obtidas, e discutir propriedades das figuras geradas. No caso da macro acima (frac_circ) o professor fornece a macro pronta e pode-se: 

1.    procurar contabilizar o número de circunferências em cada nível de aplicação (termos de uma PG);

2.    procurar uma equação para, dado n, determinar o número de circunferências que se obtém com n aplicações repetidas de frac_circ (soma dos termos da PG);

3.   procurar saber se a figura  formada com  número cada  vez  maior de aplicações, (tendendo a ) é limitada ou não (PG infinita convergente, de razão menor que 1);

4.    uma vez que a figura é limitada, procurar determinar para que figura converge (para um quadrado);

5.   procurar  formalizar o  porquê de  um  quadrado  conter  o fractal, provando que: é quadrado pois seus diâmetros encontram-se em ângulo de 90^° e ambos tem mesmo comprimento iguais a  4r, onde  r  é o raio de C₀  pois o diâmetro é:

Pode-se fazer o mesmo tipo de atividade com vários fractais conhecidos, como por exemplo, o triângulo de Sierpinski e a curva de Kock (ou floco de neve).

Exemplo 5  (Curva de Kock) Dados dois pontos  A  e  B  e um segmento  trocar o terço central do mesmo por dois lados de um triângulo equilátero e aplicar a macro recorrentemente aos quatro novos segmentos de comprimento igual a 1/3 do original.

Três passos para construção da curva de Kock

Note que, neste exemplo, existe um problema inicial que é dividir um segmento em três partes iguais. Para isso podemos utilizar uma técnica de desenho geométrico baseado no Teorema de Tales, tomando um cuidado adicional para que a macro dependa apenas de dois pontos  A  e  B.

Exemplo 6  (Triângulo de Sierpinski) Dado um triângulo formado pelos pontos  A,  B  e  C  construir uma macro que encontra os pontos médios de cada um dos lados, ligando-os por segmentos, e aplicá-la recorrentemente.

Três passos para construção do fractal triângulo de Sierpinski

Existe uma infinidade de possíveis fractais para serem explorados, seja para o estudante tentar implementar uma macro recorrentemente que o descreva ou descobrir propriedades na abordagem caixa preta. Nas figuras abaixo apresentamos dois tipos baseados em segmentos  AB, abrindo ramos de comprimento metade do original (árvores binárias). Nesse tipo de exemplo (linhas conexas) um exercício interessante é encontrar o comprimento da curva no nível de recorrência  k  (soma dos termos de uma PG).

Um fractal tipo árvore binária, com ângulo de 90^o,  três aplicações

Um fractal tipo árvore binária, com ângulo de 120^o, três aplicações

Neste texto mostramos que a geometria pode ser examinada do ponto de vista de algoritmo e com a ajuda dos programas de geometria dinâmica (GD) podemos introduzir confortavelmente esse conceito.

Além disso, se empregarmos uma abordagem tipo caixa preta, podemos trabalhar com alunos do ensino médio, fornecendo-lhes as macros recorrentes prontas e solicitando tarefas exploratórias sobre número de objetos e, no caso de fractais, qual o formato do mesmo (para que figura converge).

Referências bibliográficas

[1]   A Little History of the World Wide Web, disponível no URL:  http://www.w3.org/History.html, consultada em 13/05/2002.

[2]   Ávila, Geraldo. Os paradoxos de Zenão, RPM 39, p. 9-16.

[3]   The fractal geometry of nature, Benoit Mandelbrot, W.H. Freeman, 1983.

[4]   iMática: ambiente interativo de apoio ao ensino de matemática via internet, anais do Workshop sobre informática na escola, do XXI Congresso da Sociedade Brasileira de Computação, agosto, 2001.

[5]   SANT, Jean-Marc. O “Cabri Geomètre”, RPM 29, p. 36-40.

[6]   ÁVILA, Geraldo. As séries infinitas, RPM 30, p. 10-17.