|
|
|
|
|||
|
|
|||||
|
|
|
|
|||
|
|
|||||
José Cloves Verde
Saraiva
|
|
Introdução |
A nossa intuição geométrica de vez em quando é surpreendida pela comprovação matemática.
Nestas notas vamos provar que o poliedro regular de maior volume, inscrito numa mesma esfera, é o dodecaedro. E não o icosaedro como se esperava! Esse resultado, já conhecido dos gregos, foi desenvolvido pelo aluno Jonas de Jesus na sua monografia de conclusão de graduação e, devido algumas longas deduções trigonométricas não me conformei com a conclusão meio paradoxal! Procurei mais simplicidade!
Aqui, os cálculos serão baseados nas
coordenadas dos vértices dos poliedros regulares inscritos numa esfera de raio 1
centrada na origem de um sistema cartesiano ortogonal. As coordenadas do
dodecaedro e do icosaedro foram retiradas do artigo do Nicolau Saldanha,
Coordenadas para o Icosaedro da revista RPM 38, pp.34 – 36 [1].
Também utilizaremos a conhecida fórmula do volume de um tetraedro OABC
cujos vértices são ![]() ,
, ![]()
![]() e
e ![]() , que é a seguinte:
, que é a seguinte:
|
|
sendo que no cálculo do volume consideramos o módulo do determinante. |
|
Poliedro regulares na esfera unitária |
Os cinco poliedros regulares são bastante conhecidos:
|
|
|
|
|
|
As coordenadas dos vértices do octaedro inscrito são imediatas considerando sua simetria. As coordenadas do tetraedro e do cubo são calculadas observando a figura abaixo, na qual o cubo está centrado na origem do sistema e os eixos passam pelo centro de cada face.
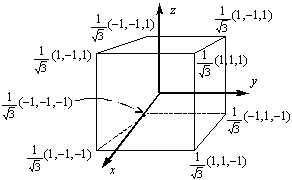
|
Tetraedro |
![]() .
.
|
Hexaedro (cubo) |
![]()
|
Octaedro |
![]() .
.
As coordenadas, a seguir, dos vértices do
dodecaedro e do icosaedro foram retiradas de [1] e normalizadas para obter os
poliedros inscritos na esfera unitária:
|
Dodecaedro |
![]()
![]()
![]()
![]()
|
Icosaedro |

|
Volume dos poliedros regulares |
Os volumes serão calculados aplicando-se
várias vezes a fórmula (1) e considerando a simetria dos poliedros centrados na
origem do sistema. Isso é feito triangulando-se as faces dos poliedros e
considerando-se tetraedros com bases nos triângulos obtidos e vértice na origem.
|
Tetraedro (4 faces triangulares) |
|
O volume do tetraedro ABCD é obtido calculando-se os volumes (iguais) dos quatro tetraedros: OABC, OABD, OACD e OBCD, ou seja, é igual a quatro vezes o volume do tetraedro OABD da figura, sendo este último calculado pela fórmula (1). |
|
![]()
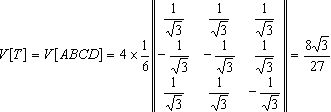 .
.
|
Hexaedro (cubo – 6 faces quadradas) |
O volume do cubo é obtido calculando-se os volumes dos tetraedros com vértice na origem e faces nos triângulos resultantes da triangularização das faces como na figura abaixo.
|
|
|
|
Como cada face dá origem a dois triângulos temos, por aplicação da fórmula (1):
|
|
|
Octaedro (8 faces triangulares) |
|
No octaedro as faces são triangulares, logo, de modo análogo aos poliedros anteriores, temos: |
|
|
Dodecaedro (12 faces pentagonais) |
Com um processo análogo aos dos poliedros anteriores, temos, para o dodecaedro:
|
|
|

|
Icosaedro ( 20 faces triangulares ) |

Por observação direta dos valores calculados para os volumes temos
![]() ,
,
o que prova que o dodecaedro é o de maior volume e, além disso,
observamos que entre os poliedros duais (cubo-octaedro e dodecaedro-icosaedro),
o de menor número de faces tem maior volume. Sabiamente, os gregos
antigos usavam os poliedros regulares numa simbologia na qual o dodecaedro
representava o Universo.
Referência bibliográfica
[1] SALDANHA, C. Nicolau. Coordenadas para o Icosaedro. RPM 38, p. 34–37.