|
SENHORA COM
CACHORRO
Andréa Vanessa
Rocha
André Toom
UFPE, Departamento de Estatística
|
 |
O Teorema Fundamental da Álgebra, ou
abreviadamente TFA, é um dos mais importantes teoremas de toda a Matemática.
Esse teorema declara o seguinte:
Toda equação algébrica

com grau
 e quaisquer coeficientes complexos tem pelo menos uma raiz
complexa. e quaisquer coeficientes complexos tem pelo menos uma raiz
complexa.
Esse famoso teorema tem várias provas
diferentes, sendo as idéias de algumas demonstrações clássicas (veja [1])
devidas a Gauss. Normalmente as demonstrações usam idéias bastante avançadas. O
que é pouco conhecido é que a demonstração clássica do teorema tem uma
explicação tão clara que pode ser apresentada para calouros na universidade ou,
até mesmo, a alunos do ensino médio se eles conhecerem os números complexos e
tiverem interesse pela Matemática. Entre os matemáticos russos, essa explicação
é conhecida como senhora com cachorro.
Seja z nossa variável que muda no
plano complexo da seguinte maneira: o módulo de z é uma constante r
e o argumento de z varia de zero até
 . Assim, z percorre um círculo no plano
complexo, cujo centro é o ponto O e o raio é r. Sabemos que
geralmente . Assim, z percorre um círculo no plano
complexo, cujo centro é o ponto O e o raio é r. Sabemos que
geralmente
 e e 
Em nosso caso, o módulo de z é
r o tempo todo, e assim o módulo de
 é é  o tempo todo. Dessa forma, como o argumento de z
vai de 0 até o tempo todo. Dessa forma, como o argumento de z
vai de 0 até  , o argumento de , o argumento de
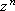 vai de 0 até vai de 0 até
 . Logo, quando z percorre um círculo com centro
O e raio r, . Logo, quando z percorre um círculo com centro
O e raio r, 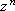 percorre n vezes o círculo com o mesmo centro e
raio percorre n vezes o círculo com o mesmo centro e
raio 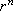 . .
Imaginemos que
 é uma senhora muito organizada, cuja casa é no ponto é uma senhora muito organizada, cuja casa é no ponto
 . Essa senhora sai da sua casa e faz um passeio saudável no
plano complexo, percorrendo n vezes o círculo perfeito com centro O
e raio . Essa senhora sai da sua casa e faz um passeio saudável no
plano complexo, percorrendo n vezes o círculo perfeito com centro O
e raio  . .
O comportamento do polinômio
 nesse processo é muito mais complicado. Imaginemos que esse
polinômio é um cachorro alegre que gosta de visitar muitos lugares, mas está
conectado com a senhora por uma coleira, como mostra o desenho a seguir. nesse processo é muito mais complicado. Imaginemos que esse
polinômio é um cachorro alegre que gosta de visitar muitos lugares, mas está
conectado com a senhora por uma coleira, como mostra o desenho a seguir.

A senhora, isto é, o termo
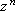 , percorre n círculos com o centro O e raio , percorre n círculos com o centro O e raio
 . O cachorro, isto é, o polinômio . O cachorro, isto é, o polinômio
 , percorre uma curva complicada, mas durante todo o passeio
está refreado por uma coleira. , percorre uma curva complicada, mas durante todo o passeio
está refreado por uma coleira.
O comprimento da coleira é o máximo da
distância entre o cachorro e a senhora, isto é, entre
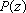 e e 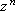 , que é o máximo do módulo da diferença entre o
polinômio , que é o máximo do módulo da diferença entre o
polinômio  e o termo e o termo
 : :
comprimento da coleira
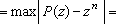
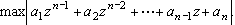
Mostremos que, quando r é muito
grande, o comprimento da coleira é muito menor que
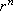 . Por exemplo, se quisermos que o comprimento de coleira
seja menor que . Por exemplo, se quisermos que o comprimento de coleira
seja menor que  , basta tomar , basta tomar
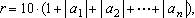 (1) (1)
pois, nesse caso, o comprimento da
coleira, ou a distância entre a senhora e o cachorro, satisfaz:

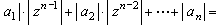
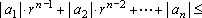

Agora temos a parte mais delicada de nosso
argumento: se o comprimento da coleira é menor que
 , o cachorro também tem que fazer n voltas em torno
de zero! Esta conclusão informal é o ponto não rigoroso da argumentação, por
isso dizemos que apresentamos uma “explicação” e não uma “prova”. Contudo, é
possível fazer a apresentação rigorosa se incluirmos definições e provas, como
no livro [2], capítulo 8, págs. 134-136. , o cachorro também tem que fazer n voltas em torno
de zero! Esta conclusão informal é o ponto não rigoroso da argumentação, por
isso dizemos que apresentamos uma “explicação” e não uma “prova”. Contudo, é
possível fazer a apresentação rigorosa se incluirmos definições e provas, como
no livro [2], capítulo 8, págs. 134-136.
Então, quando r é bastante
grande, o cachorro dá n voltas em torno do ponto O. O que
acontece quando r é pequeno? Quando
 , o cachorro fica no ponto , o cachorro fica no ponto
 durante todo o passeio e, quando r é pequeno, o
cachorro fica perto desse ponto. Se durante todo o passeio e, quando r é pequeno, o
cachorro fica perto desse ponto. Se
 , nosso teorema é evidente, pois , nosso teorema é evidente, pois
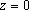 é uma raiz. Logo, podemos supor que é uma raiz. Logo, podemos supor que
 . Neste caso, quando r é bastante pequeno, o
cachorro não dá nenhuma volta em torno do ponto O. . Neste caso, quando r é bastante pequeno, o
cachorro não dá nenhuma volta em torno do ponto O.
Agora pensaremos sobre a função
 , que fornece, para cada r, o número de voltas do
cachorro em torno do ponto O. Sabemos que: , que fornece, para cada r, o número de voltas do
cachorro em torno do ponto O. Sabemos que:
A função
 é definida só quando o cachorro não visita o ponto O. é definida só quando o cachorro não visita o ponto O.
A função
 só pode tomar valores inteiros. só pode tomar valores inteiros.
Quando r é pequeno, a função
 é igual ao zero. é igual ao zero.
Quando r é grande, a função
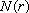 é igual ao n. é igual ao n.
Quando r cresce de um valor
bastante pequeno até um valor bastante grande, a função
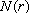 tem que crescer também. Mas como pode crescer uma função que
só tem valores inteiros? Apenas com saltos: saltando de um valor inteiro para
outro. Quando a função tem que crescer também. Mas como pode crescer uma função que
só tem valores inteiros? Apenas com saltos: saltando de um valor inteiro para
outro. Quando a função  salta, ela não está definida e isso acontece somente quando
a trajetória do cachorro cruza o ponto O. Logo, existe pelo menos um
valor de r tal que o cachorro visita o ponto O. Mas então
temos uma raiz! salta, ela não está definida e isso acontece somente quando
a trajetória do cachorro cruza o ponto O. Logo, existe pelo menos um
valor de r tal que o cachorro visita o ponto O. Mas então
temos uma raiz!
Notas
1.
Quem descobriu o TFA? Como isso aconteceu em vários estágios, não há
uma resposta simples. Vários matemáticos contribuíram nesse teorema, mas é claro
que o matemático alemão Gauss (1777–1855) foi o maior contribuidor. Ele teve
bastante interesse por ele em toda a sua vida e apresentou várias provas. Mais
informações sobre o TFA e sua história podem ser obtidas na Internet através do
www.google.com,
fazendo uma busca por Fundamental Theorem of Algebra.
2.
Quando um dos autores deste artigo, a saber A. Toom, foi aluno da
Universidade de Moscou, ouviu este argumento como parte do folclore entre os
alunos e o publicou numa revista russa [2]. O nome “senhora com cachorro” foi
tomado de um conto do escritor russo Tchekhov.
Referências bibliográficas
[1] COURANT, R. e ROBBINS, H. O que é
a Matemática? Uma abordagem elementar de métodos e conceitos. Rio de
Janeiro: Editora Ciência Moderna.
[2] FINE,
B. e ROSENBERGER, G. The Fundamental Theorem of Algebra. New York:
Springer, 1948.
|
Você Sabia |
|
Que a célebre igualdade
 , que contém os 5 números mais significativos da
Matemática, mereceu de vários matemáticos frases apaixonadas? Veja
algumas: , que contém os 5 números mais significativos da
Matemática, mereceu de vários matemáticos frases apaixonadas? Veja
algumas:
“... esta mais surpreendente
jóia..., a mais notável fórmula da Matemática.”
(R. Feynman, prêmio Nobel
de Física)
“Elegante, concisa e cheia de
significação..., ela interessa tanto ao místico quanto ao cientista,
ao filósofo, ao matemático.”
(E. Kasner e J. Newman,
autores do best seller Matemática e Imaginação.)
“Cavalheiros, isso é certamente
verdade, é absolutamente paradoxal; não podemos entendê-lo, e não
sabemos o que significa, mas provamo-lo e, portanto, sabemos que deve
ser a verdade.”
(Benjamin Pierce, eminente
matemático da Universidade de Harvard no século XIX, após deduzir a
fórmula em uma conferência.)
|
Enviado por Antonio Vladimir Martins
(MTM – UFSC). |
|
Brasileiro vira doutor em Matemática
sem fazer faculdade |
|
Jornal do
Brasil,
10/10/01: O Ministério da Educação (MEC) concedeu o título de doutor em
Matemática ao niteroiense Leonardo Macarani, 24 anos, que nunca passou por
uma universidade. O feito é inédito no Brasil. Autodidata, Macarani
abandonou o colégio na 7a série, sendo acolhido pelo
IMPA – Instituto de Matemática Pura e Aplicada, e passou a se dedicar ao
universo das ciências computacionais e da física quântica. Em pouco tempo,
o garoto prodígio, louco por Matemática desde os 10 anos, conseguiu ser
orientador do Deparatamento de Informática da Faculdade de Economia e
Administração da Universidade Federal Fluminense. Casado e amante de Led
Zeppelin e Eric Clapton, Macarani se diz "uma pessoa normal". |
|