 |
|
|
|||
 |
|||||
|
|
|
|
|||
|
|
|||||
Roberto
Ribeiro Paterlini
|
|
O problema do jogo dos discos |
Uma
escola estava preparando uma Feira de Ciências e foi pedido aos
estudantes que bolassem um jogo que servisse para arrecadar fundos. Os
estudantes observaram que no salão da Feira o piso era feito com
quadrados de 30 cm de lado, desses quadrados de Paviflex. Pensaram então
em construir discos de papelão de um certo diâmetro d
que seriam comprados pelos visitantes por R$ 1,00 cada um. O
visitante jogaria o disco aleatoriamente no piso. Se o disco, depois de
pousar no piso, tocasse um lado de um quadrado, ele perderia para a escola
o que tinha pago. Se, ao contrário, acertasse o disco inteiramente dentro
de um quadrado, ele receberia R$ 2,00 (R$ 1,00 como devolução e mais R$
1,00 como prêmio).
O
problema dos estudantes consistia em determinar o diâmetro
d dos discos de modo
que o jogo resultasse favorável à escola. Observaram que quanto menor
d, melhor para o jogador,
e quanto maior d,
melhor para a escola. O favorecimento para a escola não deveria
ser exagerado, pois, se o jogo fosse muito desfavorável para o jogador,
ninguém iria querer jogar. Resolveram que uma probabilidade de 60% favorável
à escola seria adequada.
Pergunta
1: Como determinar o
valor de d
que resulta em uma probabilidade de 40% favorável ao jogador e de
60% à escola?
Pergunta
2: Qual será, em média,
o ganho da escola se 500 discos forem vendidos na feira?
Pergunta
3: Se os quadrados do
piso têm lado l, qual a fórmula para o valor de
d que resulta numa probabilidade
p para o jogador?
Pergunta
4: O que muda no jogo
se for feita a seguinte modificação: se o bordo do disco tangenciar o
lado de um quadrado, a jogada é favorável ao jogador. Qual a
probabilidade de ocorrer esse caso?
|
Solução
do problema do jogo dos discos |
Resposta da Pergunta 1
Para
obtermos uma solução exata, podemos resolver primeiro a pergunta 3 e
depois especificar os valores
cm e
Isso está feito logo
abaixo, onde
podemos ver que o diâmetro procurado é
Uma solução
aproximada pode ser obtida simulando-se o jogo com discos de vários diâmetros.
Para cada diâmetro fazemos o quociente do número de acertos do jogador
pelo número de jogadas. Colocamos os dados num gráfico cartesiano em que
o eixo dos x
representa o diâmetro dos discos e o eixo dos
y
representa a probabilidade de o jogador ganhar. Unindo-se os pontos
assim conseguidos, obtemos uma curva que se assemelha a uma parte do gráfico
de uma função quadrática
Através desse gráfico
procuramos o valor de d
para o qual resulta
Esse é o valor
aproximado. Abaixo apresentamos os dados de um experimento realizado por
estudantes, no qual foi obtido
|
Resposta
da Pergunta 2 |
Se
500 discos forem vendidos na feira, a arrecadação bruta será R$ 500,00. Supondo que em 40% das jogadas (200 jogadas) os
jogadores ganhem, a escola pagará R$ 400,00. Sobrará R$ 100,00 para a
escola.
|
Resposta
da Pergunta 3 |
Seja
l a medida do lado do quadrado do piso e seja
d,
o diâmetro do disco.
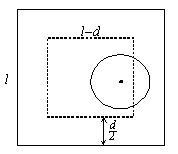
Construindo um quadrado de lado
simetricamente disposto
dentro do quadrado de lado l
(ver figura), vemos que o jogador ganha se o centro do disco cair
no interior do quadrado de lado
Sob
condições ideais podemos supor que lançar o disco aleatoriamente no
piso é o mesmo que lançar seu centro aleatoriamente. Assim, a
probabilidade p
de o jogador ganhar é a mesma probabilidade de um ponto, lançado
aleatoriamente dentro do quadrado de lado
l, cair dentro do quadrado de lado
Da definição de
probabilidade geométrica (veja [3]) temos
um
disco de diâmetro d,
lançado
aleatoriamente, cair inteiramente no interior do quadrado de lado
l.
Dada uma probabilidade p,
com
resolvendo a equação
em
d,
obtemos
Lembrando que
, temos
Esse é o diâmetro do
disco que resulta em uma probabilidade
p
em favor do jogador.
Podemos
agora encontrar a resposta exata da Pergunta 1. Fazendo
e
, obtemos
Em valores aproximados
resulta
cm.
é um zero duplo de
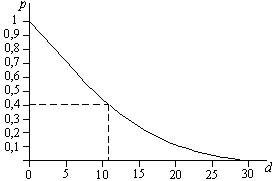
As
duas linhas pontilhadas na figura acima mostram como se obtém
graficamente o valor de d
tal que
|
Resposta
da Pergunta
4 |
Teoricamente
nada muda. A probabilidade de o disco tangenciar o lado de um quadrado é
zero, embora a contagem desses casos no método experimental dependa do
observador das jogadas.
|
Comentários
sobre o uso do jogo dos discos em sala de aula |
Participando
de um projeto dos Departamentos de Matemática e Física da UFSCar tivemos
a oportunidade de orientar um grupo de professores que aplicaram o
problema do jogo dos discos em suas escolas.
|
d |
p |
Para
resolver o problema por experimentação foram construídos discos
de madeirit ou de borracha com diâmetros 4, 6, 8, 10, 12 e 14 cm. Os
professores observaram que devem ser feitos pelo menos 200 lançamentos
para cada diâmetro e para facilitar a experiência foram feitos 10
discos de cada diâmetro. |
|
4 |
75,5% |
|
|
6 |
68,5% |
|
|
8 |
62% |
|
|
10 |
50% |
|
|
12 |
38% |
|
|
14 |
32% |
Os
resultados obtidos em uma classe da 2a série estão
dispostos na tabela ao lado, sendo d o diâmetro dos
discos, em cm, e p a probabilidade de o
jogador ganhar.
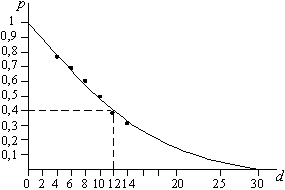
No
gráfico estão dispostos os pontos obtidos. Os estudantes, usando uma
folha de papel quadriculado e uma régua, desenharam a curva que lhes
pareceu ser a que melhor se aproximava dos pontos dados e obtiveram a solução
(ligeiramente diferente
do que obtivemos no gráfico). Ao fazer nosso gráfico (acima), usamos o
aplicativo computacional Maple V para
obter a função quadrática que mais se aproxima dos pontos dados.
Acrescentamos na lista dos estudantes os pontos
e
A função obtida foi
Resolvendo
a equação
em
d,
temos
|
Fazendo
conexões |
No
problema do jogo dos discos podemos considerar pavimentações de outros
tipos para o piso onde serão lançados os discos, fazendo conexões com
outras áreas da Matemática.
Consideremos
as pavimentações chamadas mosaicos regulares do plano. Conforme vemos em
[1], p. 3, são pavimentações constituídas por polígonos regulares de
um único tipo e satisfazendo as condições:
a) quando dois polígonos se intersectam, essa interseção é um
lado ou um vértice comum; b)
a distribuição dos polígonos ao redor de cada vértice é sempre a
mesma. Os únicos mosaicos regulares do plano são os constituídos por
triângulos equiláteros, quadrados ou hexágonos regulares.
Vamos
aplicar nosso jogo dos discos a esses tipos de pavimentação. O caso de
mosaicos formados por quadrados já foi estudado acima. Vejamos os outros
dois casos.
|
Suponhamos
que o piso do jogo dos discos seja pavimentado com peças na forma
de triângulos equiláteros de lado
l. |
|
|
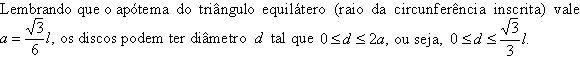
No
interior do triângulo equilátero de lado
l
dispomos um triângulo equilátero de lado t,
com lados paralelos ao triângulo maior, de modo que a distância
entre o lado do triângulo maior
|
|
Podemos
verificar que a relação entre l
e t
é
Lembrando que a razão
entre as áreas de duas figuras semelhantes é igual à razão entre os
quadrados dos lados, a probabilidade de um disco de diâmetro
d,
lançado aleatoriamente no piso, cair inteiramente dentro do triângulo
de lado l
é
o caso de o piso ser pavimentado com triângulos
equiláteros.
Se
o piso for pavimentado com peças na forma de hexágonos regulares, a
probabilidade de um disco de diâmetro
d, lançado aleatoriamente no piso, cair inteiramente dentro de um hexágono
é
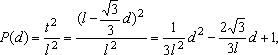
com
Resolvendo a equação
em
d,
temos
Como
, vem
Essa é a solução
para o caso de o piso ser pavimentado com hexágonos regulares.
Outros
tipos de pavimentação podem ser considerados.
Referências
bibliográficas
[1]
RPM 40. Mosaicos
no plano, Sérgio Alves e Mário Dalcín.
[3]
RPM 34. Probabilidade geométrica,
Eduardo Wagner.
|
RPM:
Nota histórica sobre Buffon e o problema dos ladrilhos |
Georges
Louis Leclerc, Conde
de Buffon, nasceu em 7 de setembro de 1707, em Montbard, na França, e
morreu em 16 de abril de 1788, em Paris. Nascido
na aristocracia, estudou Medicina e Direito. Mostrou interesse pela Matemática,
tendo descoberto sozinho a Fórmula do Binômio e mantido correspondência
com Cramer sobre Mecânica, Geometria, Probabilidade, Teoria dos Números
e Cálculo Diferencial e Integral. Mas era a Natureza a sua paixão.
Dedicou-se principalmente à História Natural, tendo sido o maior responsável
pelo crescimento do interesse pela História Natural na Europa, no século
XVIII. O
jogo do ladrilho Era
bastante jogado pelas crianças francesas no século XVIII. Uma pequena
moeda de raio R é lançada ao
acaso em um chão coberto por ladrilhos quadrados de lado
l
(l>2r) Buffon
notou que a probabilidade de a moeda cair inteiramente dentro de um
ladrilho era a probabilidade de o centro da moeda cair dentro de um
quadrado de lado
Essa probabilidade é a razão entre as áreas do quadrado e do ladrilho,
pois a probabilidade de o centro da moeda cair em uma região é
proporcional à área dessa região. Portanto, a
probabilidade de a moeda cair inteiramente dentro de um ladrilho é
|
