José Paulo Carneiro
jpqc@uninet.com.br 

     1.  Introdução

A figura 1 apresenta um gráfico que pode descrever a seguinte situação, muito comum em modelagem: um pesquisador está investigando como uma certa quantidade  y  (por exemplo, o custo de um produto, ou a voltagem nos terminais de um condutor, etc.) varia com outra quantidade  x  (o número de unidades produzidas, ou a corrente que atravessa o condutor, etc.), e as observações parecem sugerir que o gráfico é ou “deveria ser” uma reta, sendo que os desvios em relação a essa suposta reta podem ser atribuídos talvez a flutuações ou imprecisões dos instrumentos de medição. Trata-se então de saber qual é a reta que melhor se “ajusta” a esse conjunto de dados. Como se faz isso?


figura 1

Suponhamos que tenham sido feitas  n  observações do fenômeno, medindo-se os valores de  x  e os correspondentes valores de  y,  obtendo-se os pontos  .  Queremos determinar uma reta, de equação  ,  que de uma certa maneira seja a reta “mais próxima possível de todos os  n  pontos”. Considere então uma reta de equação  .  Para cada ponto  ,  temos o valor observado    e o valor “esperado”  ,  isto é, o valor que  y  assumirá se o modelo representar corretamente a realidade.

O “desvio” cometido, para cada ponto  ,  é a diferença entre o valor esperado e o valor observado,  isto é:

  (figura 2).

         figura 2

Uma medida que pareceria bem natural do “desvio total” seria a soma dos valores  absolutos  dos  desvios individuais. No entanto, algumas razões técnicas (ver Apêndice) recomendam o uso da soma dos quadrados dos desvios individuais, ou seja,

  ou, para quem prefere a notação de somatório: mínimos quadrados”. Portanto, o nosso problema se reduz a:

Determinar  m  e  p  de modo que seja mínima a soma

Note-se que escrevemos    para deixar bem claro que    são dados do problema. As incógnitas são  m  e  p.  Portanto, trata-se de determinar o valor mínimo de uma função de duas variáveis. Tal problema costuma ser abordado apenas em cursos superiores, após o estudo do Cálculo Diferencial de várias variáveis. O objetivo do presente artigo é mostrar que ele pode perfeitamente ser resolvido por métodos mais elementares, usando somente o que é conhecido no ensino médio sobre funções quadráticas. Comecemos com um exemplo de caráter didático, para concretizar.  

 

     2.      Exemplo  

Suponha que os dados sejam         e   (faça uma figura!). Neste caso:   (confira as contas!).

Como determinar  m  e  p  de modo que    seja mínimo? A expressão de    já sugere qual é a dificuldade do problema. Repare que, se não existisse o termo  18mp  (isto é, se o coeficiente de  mp  fosse 0), o problema seria bem mais fácil, ou melhor, seria um problema conhecido, já que nesse caso    seria a soma de duas funções quadráticas independentes (uma em  m,  outra em  p).  Bastaria então determinar os valores de  m  e  p  que, separadamente, tornassem mínimos os valores dessas funções quadráticas, um problema usual no ensino médio.

Mas de onde vem o coeficiente de  mp?  Se o leitor tiver feito as contas do exemplo dado, desenvolvendo os quadrados e depois somando, deve ter observado que esse coeficiente foi obtido como   . De um modo geral, no caso de n pontos  quaisquer, esse coeficiente seria, analogamente:

Isso pode sempre ser arranjado: basta fazer uma translação horizontal do eixo  Y  de modo que a nova origem seja o ponto   (figura 3). Então cada abscissa    mudará para    mantendo-se as ordenadas  .

Logo, a média dos    será:

figura 3



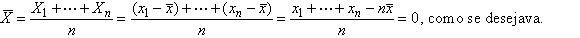
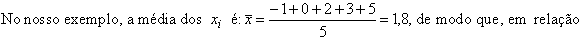
a esse novo sistema de coordenadas, as coordenadas dos pontos    passam a ser:     e  .

Vamos então refazer o problema em relação a esse sistema de coordenadas, isto é,  

  Observe que não há termo em  MP,  porque  Como é conhecido a respeito de funções quadráticas,    é mínimo quando

Retornando ao sistema inicial (isto é, substituindo  X  por  ), obtém-se:

(figura 4), que é a procurada reta dos mínimos quadrados para o dado conjunto de pontos do exemplo.

figura 4

     3.    O caso geral  

O professor pode optar por refazer esse tipo de procedimento em cada caso: 

(i) calcula-se a média    dos  ;  (ii) translada-se a origem para  ,  o que equivale a trocar cada    por  ;  (iii) determina-se a equação da reta dos mínimos quadrados,
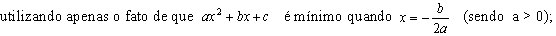
 (iv) retorna-se ao sistema de coordenadas primitivo.

Mas também pode-se aplicar esse procedimento ao caso geral e chegar a uma fórmula. O raciocínio para  n  pontos genéricos    é análogo e vai resumindo agora (usando a notação de somatório, e onde todos os somatórios que aparecem são de 1 até  n).

que dá os coeficientes  m  e  p  da reta dos mínimos quadrados para os pontos 

Observações:


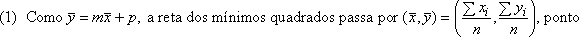
que é chamado o centro de gravidade dos  n  pontos 

(2) Há outras expressões interessantes para m (e conseqüentemente para p), que o
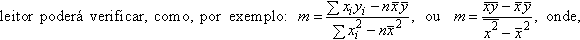
naturalmente,    é a média aritmética dos    e    é a média aritmética dos 

   

     4.  Apêndice  

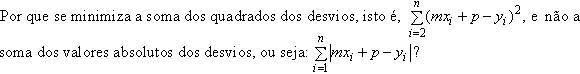Em primeiro lugar, é claro que lidar com uma função quadrática, que é uma função polinomial, com um gráfico suave, sem “bicos” (isto é, derivável), é muito mais fácil do que lidar com uma função modular, com “bicos” (isto é, não derivável).

Mas não é só isso. O ponto-chave da questão é que quando os dados   são tais que os desvios podem ser considerados aleatórios, no sentido próprio e estatístico da palavra, então os coeficientes da reta dos mínimos quadrados têm interpretações estatísticas precisas, em termos de variâncias, covariâncias, correlações e outros conceitos estatísticos, o que possibilita a aplicação de todo o ferramental estatístico à explicação dos fenômenos envolvidos. Nesse caso, a reta dos mínimos quadrados também é chamada, por motivos históricos, de reta de regressão.  

 

     5.  Comentário bibliográfico  

Em qualquer livro de Estatística, sob o título ajustamento ou regressão, podem encontrar-se outros detalhes sobre esse assunto, que também aparece como exercício ou aplicação em livros de Cálculo Diferencial.