Eduardo Wagner
Comitê Editorial da RPM

Em todo poliedro convexo com  V  vértices,  A  arestas e  F  faces, vale a relação  .  Este é o Teorema de Euler para poliedros. A simplicidade do enunciado, a sua generalidade e a facilidade de ilustrá-lo com belos desenhos o tornam atraente, ou mesmo fascinante, para o estudante. Ao longo da história (o teorema foi descoberto em 1758), diversas demonstrações apareceram, mas nem todas corretas ou completas.

Na RPM 03, num artigo do Prof. Zoroastro Azambuja Filho, encontra-se uma demonstração elementar e muito bonita do teorema; o leitor pode ver também a mesma idéia na demonstração que se encontra no volume 2 do livro Matemática do ensino médio, publicado pela SBM.

A pergunta natural que se impõe é a seguinte: dados três números naturais  V,  A  e  F  tais que   ,  existe sempre um poliedro convexo com  V  vértices,  A  arestas e  F  faces? A resposta é gritantemente não. Por exemplo,  V = 7,  A = 9  e  F = 4  satisfazem a relação de Euler  ,  mas não são números de nenhum poliedro, uma vez que com 4 faces só existe o tetraedro, que tem 4 vértices e 6 arestas.

Portanto, que condições os números  V,  A  e  F  devem satisfazer, além da relação de Euler, para que possamos garantir a existência de um poliedro com esses números de vértices, arestas e faces? Obter a resposta para essa pergunta é o objetivo deste artigo.
 

Imagine um poliedro (ver a definição no Apêndice)  P  com todas as suas faces triangulares (como o tetraedro, por exemplo). Nesse caso,     3F = 2A,  uma vez que cada aresta é lado de exatamente duas faces. Entretanto, se  P  possui alguma face não triangular, então 3F < 2A.

É portanto condição necessária que  .                    (1)

Imagine agora que, no poliedro P, cada vértice seja ponto comum a três arestas (como no cubo, por exemplo). Nesse caso, 3V = 2A,  pois, contando as arestas que incidem em cada vértice, teremos contado cada uma duas vezes. Entretanto, se  P  possui algum vértice onde incidem mais de 3 arestas, teremos 3V < 2A.

É portanto condição necessária que .                     (2)

Se  P  é convexo, então    ou    e, usando (1),  obtemos   ou seja,    Usando  (2),  obtemos 

Portanto, para a existência de um poliedro convexo com  V  vértices,  A  arestas e  F  faces, é necessário que, além da relação de Euler, e de que ,  tenhamos:    e 

Se o número de arestas é pequeno, podemos facilmente investigar o aspecto de alguns poliedros. Por exemplo: Como são os poliedros que possuem  10  arestas?

Considerando as condições que acabamos de estabelecer, se A = 10, devemos ter    e  .

Logo,  F = 6  e  V = 6.  Veja como eles são:

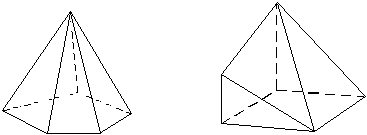
O primeiro é uma pirâmide pentagonal e o segundo possui duas faces quadrangulares e quatro faces triangulares.

Observe que não podemos construir um poliedro, com as características estabelecidas, somente com faces triangulares. Como vimos antes, se um poliedro possui apenas faces triangulares, então  3F = 2A,  o que não ocorre aqui.

Vamos prosseguir para encontrar condições suficientes para a existência de um poliedro convexo com  V  vértices,  A  arestas e  F  faces.

Representaremos por  (V, A, F)  qualquer um dos poliedros da família de todos os poliedros que possuem  V  vértices,  A  arestas e  F  faces. Por exemplo,  (6, 10, 6)  representa qualquer um dos dois poliedros que estão ilustrados na figura anterior.  

Existe um poliedro convexo com V vértices, A arestas e F  faces se, e somente se:

i)   

ii)  

iii) 

iv) 

Prova: Inicialmente observamos que as condições  i)  e  iv)  podem ser obtidas  de  ii)  e  iii);  logo, não seria necessário escrevê-las, mas optamos por fazê-lo para maior clareza.

Já vimos que as condições são necessárias. Vamos então provar a suficiência.

a) Inicialmente, definimos os poliedros (famílias) que chamaremos de primitivos. São os seguintes:

(4, 6, 4): o tetraedro,

(5, 8, 5):    a pirâmide de base quadrangular,

(6, 10, 6):  os poliedros que ilustramos na página anterior.

b)  Vamos agora definir duas transformações a serem aplicadas nos poliedros primitivos:

A transformação denotada por  (2, 3, 1)  acrescenta a um poliedro dois vértices, três arestas e uma face. Ela é realizada ajustando as arestas que incidem em um vértice, acrescentando uma nova face triangular como mostra a figura a seguir. As arestas e os vértices novos estão em negrito.

A transformação denotada por  (1, 3, 2)  acrescenta a um poliedro um vértice, três arestas e duas faces. Ela é realizada, introduzindo duas faces triangulares novas a partir de duas arestas adjacentes de uma face do poliedro. As arestas novas e o vértice novo estão em negrito.

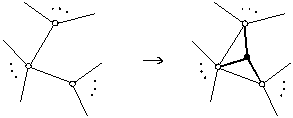
A idéia dessas transformações deve-se a Edward Bender, da Universidade da Califórnia, que as publicou no artigo “The number of three dimensional convex polyhedra”, da American Mathematical Monthly, volume 94, January, 1987. Washington, D.C.

Os poliedros primitivos satisfazem as condições  i)  a  iv)  e, aplicando-se a eles qualquer número de transformações  (1, 3, 2)  ou           (2, 3, 1),  continuamos obtendo poliedros que satisfazem essas condições. Por exemplo, se aplicarmos  x  vezes a transformação  (1, 3, 2)  ao poliedro  (4, 6, 4),  obtemos o poliedro ,  que claramente satisfaz a condição  i);

satisfaz  ii), pois  4 + x – 6 – 3x + 4 + 2x = 2;

satisfaz  iii), pois  ;

satisfaz  iv), pois  .

Um trabalho análogo mostra que os três poliedros primitivos submetidos às transformações  (1, 3, 2)  e  (2, 3, 1)  conservam as condições i)  a  iv).

A parte final vem a seguir, onde mostraremos que se  V,  A,  e  F  satisfazem  as condições  i)  a  iv),  existe  um  poliedro  com  esses números de vértices, arestas e faces.

c) Dado  (V, A, F),  satisfazendo i)  a  iv),  existem inteiros não negativos  x  e  y  e existe um poliedro primitivo    tais que

, ou seja,  (V, A, F)  pode ser construído a partir de um dos poliedros primitivos.

Para provar isso, observe inicialmente o número de arestas dos poliedros primitivos. No primeiro, o número de arestas é múltiplo de  3,  no segundo, deixa resto  2  quando dividido por  3  e, no terceiro, deixa resto  1 quando dividido por  3. Veja também que, para quaisquer  x  e  y,  o número  A  permanece inalterado (módulo 3),  ou seja, seu resto na divisão por  3  permanece o mesmo.

Suponhamos que  A 0 (mod 3),  ou seja,  A  é divisível por  3.

Nesse caso, mostraremos que existem inteiros não negativos  x  e  y  tais que

,

o que é equivalente ao sistema:

Se  x  e  y  satisfazem a primeira e a terceira equações, então também satisfazem a segunda, uma vez que somando a primeira e a terceira equações obtemos, usando a relação de Euler,

Devemos ainda mostrar que as soluções  x  e  y  do sistema

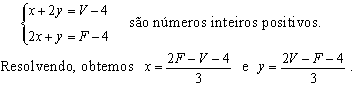
Vamos provar que  x  é inteiro:

Como estamos no caso A 0 (mod 3), temos A + 2 2 (mod 3) ou  2(A + 2) 1 (mod 3).

Como  3V 0 (mod 3)  e  4 1 (mod 3), temos

2F V 4 = 2F + 2V 3V 4 = 2(A + 2) 3V 4   = 0(mod3).

Assim,    é divisível por  3,  o que mostra que  x  é inteiro.

Da mesma forma, mostra-se que  y  é inteiro.

Com procedimento análogo mostra-se que, se  A 1 (mod 3),  conseguimos encontrar  x  e  y  inteiros tais que:

e que, se  A º 2 (mod 3),  conseguimos encontrar  x  e  y  inteiros positivos tais que

.  A primeira igualdade decorre da relação de Euler e a segunda da hipótese iii). Portanto,  x  não é negativo e, da mesma forma, mostra-se que  y  também não é negativo, completando a demonstração.

NOTA DA RPM: A idéia deste artigo foi inicialmente apresentada pela professora Silvana L. Vincenzi Bortolotti – CEFET – Medianeira – PR, que enviou à RPM uma proposta de artigo tratando do assunto. Agradecemos a ela o interesse pela RPM e por ter chamado nossa atenção sobre o tema.

O que significa a palavra poliedro neste artigo

Poliedro pode ser definido com diferentes níveis de generalidade. Como estamos interessados aqui na relação de Euler, vamos inicialmente definir poliedros convexos, para os quais a relação vale.

Um poliedro convexo é uma reunião de um número finito de polígonos planos de modo que:

a)      Cada lado de um polígono é também lado de um, e apenas um, outro polígono.

b)      O plano que contém um desses polígonos deixa todos os outros em um mesmo lado.

Cada polígono é denominado face do poliedro, cada lado comum a dois desses polígonos é uma aresta do poliedro e cada vértice de um desses polígonos é também vértice do poliedro.

É verdade que todo poliedro convexo satisfaz a relação de Euler, mas é fácil achar exemplos de poliedros não convexos para os quais ela ainda vale, como o poliedro  P,  na  figura a seguir. Observe agora o poliedro   à direita.

Diremos que os poliedros P e  são equivalentes. O poliedro  P  não é convexo, mas    é convexo. A idéia que vem a seguir é a de transformar um poliedro em outro, de forma suave. A definição (nada formal) é a seguinte:

Dois poliedros são equivalentes se existe uma deformação contínua que transforma qualquer um deles no outro.

No caso dos poliedros  P  e    acima, a deformação consiste em “puxar” o vértice da pirâmide interior para fora.

Com essa ferramenta, podemos modificar a forma de um poliedro como se ele fosse de borracha, sem nos preocuparmos se as faces são planas ou se as arestas são retas.

Em todo o artigo, a palavra poliedro designa um objeto que é equivalente a um poliedro convexo. Isso permite ler a demonstração sem a preocupação da convexidade a cada instante.

No livro Meu professor de Matemática, do prof. Elon Lages Lima, o leitor encontrará material interessantíssimo sobre poliedros, sua história, a dificuldade em conseguir uma definição e duas demonstrações do teorema de Euler.

Referência bibliográfica:

BENDER, E. A. The number of three dimensional convex polyhedra. The American Mathematical Monthly, volume 94, number 1, January, 1987. Washington, D.C.