Cláudio Possani
Élvia Mureb Sallum
Flávio Wagner Rodrigues
IME–USP
Soluções e Sugestões
RPM – Problemas
Caixa Postal 66281
05315-970 São Paulo, SP
|

|
198.
Para
cada número natural, n, n
 0, determinar os inteiros a, b, c e
d, 0, determinar os inteiros a, b, c e
d, 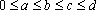 , tais que , tais que
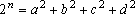 . .
(Olimpíadas Argentinas.)
200.
Seja f: IN ® Z uma função tal que
i)
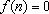 se se
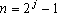 , ,
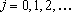 . .
ii)
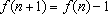 se se
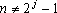 , ,
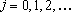 . .
Demonstre que, para qualquer
 IN, existe IN, existe
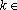 Z, Z,
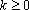 tal que tal que
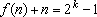 . Calcule . Calcule
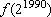 . .
(Olimpíadas
Ibero-Americanas de Matemática.)
|
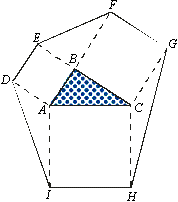
200. Sobre os lados de um triângulo ABC são construídos
quadrados e, em seguida, ligam-se os vértices, formando-se um hexágono
DEFGHI. Sendo AB =
13, BC = 14 e
AC = 15, determine a
área desse hexágono.
(Enviado por J. Cláudio M. Velloso,
RJ.) |
 |
|
1. Joaquim deve transportar alguns
sacos para um depósito, recebendo R$0,20 por quilo transportado. Os sacos
podem pesar 30, 40 ou 50 kg e ele demora 8, 12 ou 20 minutos para
transportá-los, respectivamente. Qual é a quantia máxima que o Joaquim
poderá ganhar em exatamente uma hora de trabalho?
(Olimpíadas Portuguesas de Matemática, 8º 9º anos.)
|
 |
2. 36 alunos de uma determinada escola prestaram exames vestibulares em duas
universidades, A e B, sendo que, desse grupo de alunos, todos
os aprovados em A também foram aprovados em B e o número de
aprovados em B foi o triplo do número de aprovados em A. Se
foram aprovados menos da metade e mais de um terço desses alunos, quantos não
foram aprovados em nenhuma das duas universidades?
|
3. Vou ganhar dois cães, um branco e
um preto. Sei que um deles é macho. Qual é a probabilidade de ambos serem
machos?
(Enviado por Jorge
Luis R.Silva, CE.) |
 
|
|
(Ver
respostas na
seção "Os primos esquecidos")
|
Soluções dos problemas propostos na RPM 45 |
190.
Escreva o número 512 como uma soma
de dois números inteiros positivos, um dos quais é múltiplo de 11 e o outro é
múltiplo de 13. Seria possível resolver o problema se fosse solicitado que um
fosse múltiplo de 15 e o outro múltiplo de 21? Justifique sua resposta.
Solução
Supondo que existam inteiros positivos a e
b tais que
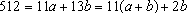 , ,
concluímos que
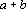 é um número par. Além disso, é um número par. Além disso,
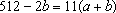 e, então, não é difícil verificar que o maior valor
possível para e, então, não é difícil verificar que o maior valor
possível para 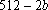 é 506 e o menor é 440, o que implica é 506 e o menor é 440, o que implica
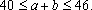 Resultam as possibilidades: Resultam as possibilidades:
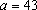 e e
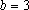 ; ;
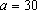 e e
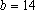 ; ;
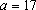 e e
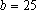 ; ;
 e e
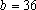 . .
A resposta para a pergunta “Seria possível resolver
o problema se fosse solicitado que um fosse múltiplo de 15 e o outro múltiplo de
21?” é:
Não existem a, b inteiros positivos
tais que
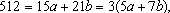 pois 512 não é divisível por 3. pois 512 não é divisível por 3.
(Solução enviada por diversos leitores.)
191.
Determine três números inteiros
positivos, distintos, cujos quadrados estejam em progressão aritmética.
Justifique sua resposta.
Solução:
É fácil exibir três números com a propriedade
exigida, como, por exemplo, 1, 5 e 7 (PA: 1, 25, 49). Vamos, agora,
apresentar uma solução genérica para o problema.
Sejam a, b, c inteiros
positivos, distintos tais que
 , ,
 e e
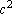 estejam em PA. Mostraremos que existem x,
estejam em PA. Mostraremos que existem x,
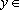 IN tais que IN tais que
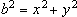 . De fato: . De fato:
Como
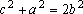 , temos que , temos que
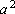 e e 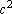 são ambos pares ou ambos ímpares, logo, o mesmo acontece com
a e c. são ambos pares ou ambos ímpares, logo, o mesmo acontece com
a e c.
Assim, existem x,
y  IN tais que IN tais que
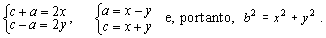
Reciprocamente, sejam b, x, y inteiros positivos tais
que 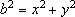 . .
As soluções naturais de
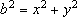 são dadas (ver RPM 7, p.49 e RPM 18, p.10),
por: são dadas (ver RPM 7, p.49 e RPM 18, p.10),
por:
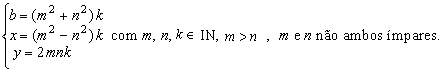
Se 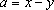 e e
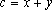 , mostremos que , mostremos que
 , ,
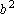 e e
 estão em PA. De fato, temos: estão em PA. De fato, temos:
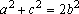 ; ;
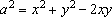 ; ;
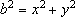 e e
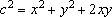 . .
Logo, as triplas (a, b, c) de inteiros positivos,
distintos, cujos quadrados estão em PA, são dadas por
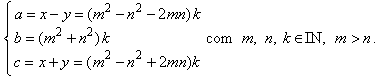
192.
Sejam A1, A2, A3,
A4, A5 e A6 os
vértices de um hexágono convexo equilátero, tal que
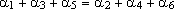 , onde , onde
 é a medida do ângulo interno no vértice Ai.
Prove que é a medida do ângulo interno no vértice Ai.
Prove que 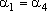 , ,
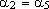 e e
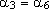 . .
O
hexágono equilátero A1 A2 A3 A4 A5 A6 é tal que
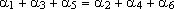 . Não podemos admitir outras condições adicionais
como regularidade, paralelismo entre lados, etc. . Não podemos admitir outras condições adicionais
como regularidade, paralelismo entre lados, etc.
Seja O A1 A3
o triângulo obtido pela reflexão do triângulo A1 A2
A3 em torno do lado A1 A3.
Os triângulos P A3
A5 e Q A5
A1 são obtidos de forma análoga.

Como 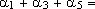 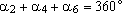 , segue que , segue que
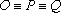 , e o hexágono inicial fica decomposto em três losangos. , e o hexágono inicial fica decomposto em três losangos.
Além disso, na figura temos:
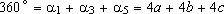 , o que implica , o que implica
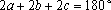 e e
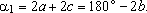 Mas no triângulo O
A3
A5, Mas no triângulo O
A3
A5,
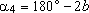 , logo, , logo,
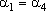 . .
De modo análogo mostra-se que
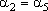 e e
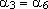 . .
(Solução adaptada da enviada por Carlos Alberto da Silva Vitor, RJ.)
193.
Para que valores de n é possível construir uma seqüência de
segmentos A1A2,
A2A3, ...
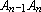 , ,
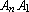 tais que tais que
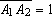 , ,
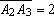 , ... , ...
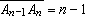 , ,
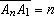 e tais que quaisquer dois segmentos adjacentes sejam
perpendiculares? e tais que quaisquer dois segmentos adjacentes sejam
perpendiculares?
|
Relação dos leitores que
enviaram soluções dos problemas da RPM 45 |
|
Amaro José de Oliveira Fo,
PE – 190 |
Leonardo Barroso, CE – 190 |
|
Anderson A. de Araujo, RJ –
190, 192 |
Lhioko S. Tayra, SP – 190, 191 |
Antonio Ferreira
Sobrinho, SP – 190
|
Luciano Marinho Fo, PE –
190, 191 |
|
Antônio Matos dos Santos, PR – 190, 191 |
Luís Felipe de Araújo, PB – 190, 191 |
Carlos A. Gomes, RN –
190
|
Luiz
César Niehues, SC – 190
|
Carlos
A.S. Victor, RJ – 190, 191, 192
|
Marcelo da Silva
Mendes, PI – 190, 192
|
Deise Leandra
Fontana, PI – 190, 191, 192
|
Mauro Felix de Souza,
RJ – 190
|
Florival Carmo de
Sousa, GO – 190, 191
|
Milton
Dini Maciel, SP – 190 |
Fernando Carvalho
Ramos, RS – 191
|
Pedro Sérgio S. de
Sousa, SP – 190, 191
|
Francisco das C. S.
Carvalho, PI – 191
|
Pierre
Bedouch, MG – 190
|
Geraldo Perlino Jr.,
SP – 190, 191
|
Rizio Sant’Ana, MG – 190, 191 |
Guita Nascimento, RJ
– 190
|
Robério L. de Carvalho, CE – 190, 192 |
Jaime Oliveira, SE –
190
|
Roberto Luís Dotto,
SP – 190, 191
|
Joaquim M. Coutinho,
RJ – 190, 191
|
Ruy
Carlos Miritz, RS – 190
|
João Socorro P.
Ferreira, AP – 190
|
Sebastião M. Santos,
MG – 190, 191
|
Jorge F. dos Santos, RJ – 190, 191, 192
|
Tsunediro Takahashi, SP – 190
|
José Cláudio M.
Velloso, RJ – 190, 191
|
Valdir Ferreira
Lobo, CE – 190, 191
|
|
José Henrique Piccirillo, SP
– 190, 191 |
Victor
Chakur, SP – 190, 191
|
|
José Hernandes, SP – 190, 191 |
Wanderley Gamba, SP –
190, 191
|
|
Notas da RPM:
|
|
1.
A
RPM agradece mais uma preciosa colaboração de Gilberto
G. Garbi que nos enviou a solução do problema 191
enriquecida com comentários a respeito do tema. O material será
examinado pelo Comitê Editorial da revista para possível publicação.
2.
Na relação de
acertadores da RPM 46
erramos o nome do leitor
Macelo da Silva Mendes (publicamos Marcelo da Silva Mendes). A ele, nossas
sinceras desculpas.
|
|