|
Novo Lançamento da SBM
Exame de Textos
Análise de Livros de Matemática para o
Ensino Médio
Elon Lages Lima
(editor)
(470 páginas) Rio de Janeiro 2001
Publicação da Sociedade Brasileira de Matemática.
Estrada Dona Castorina 110, CEP 22460-320, Rio de Janeiro, RJ.
Fones (0xx21) 529-5073, 529-5076.
http:// www.sbm.org.br
e-mail: sbm@impa.br |
 |
Analistas: Augusto Cesar Morgado,
Edson Durão Judice, Eduardo Wagner, Elon Lages Lima,
João Bosco Pitombeira de Carvalho, José Paulo Quinhões Carneiro,
Maria Laura Magalhães Gomes, Paulo Cezar Pinto Carvalho.
A Sociedade Brasileira de Matemática acaba
de publicar o livro intitulado Exame de Textos.
Ele contém uma apreciação de 36 volumes, constituindo 12 coleções de livros
didáticos usados no ensino médio de Matemática nas escolas brasileiras. Os
exames e as respectivas conclusões foram feitos por oito professores de
reconhecida experiência no ensino. O projeto foi patrocinado pela sociedade
VITAE, uma organização privada à qual a Educação em nosso país muito deve, com o
apoio do IMPA, que muito corretamente vê o ensino básico como uma etapa
indispensável para a pesquisa, e da SBM, cujo suporte às iniciativas que visem à
boa qualidade do ensino de Matemática é constante e incentivador.
O total de páginas lidas, analisadas,
discutidas em conjunto e depois resenhadas excede a 15 000. Para ser exato, esse
número deveria ser multiplicado por 2, pois dois analistas se responsabilizaram
pelo escrutínio e redação definitiva da resenha de cada texto.
O resultado final do trabalho é
apresentado num livro de quase 500 páginas, que a SBM põe agora à disposição dos
professores, estudantes universitários e, de modo geral, de todos aqueles
interessados em questões de ensino.
Seria um engano pensar que se trata
meramente de uma série enfadonha de 36 resenhas que se limitam a descrever o
conteúdo de cada livro considerado, ocasionalmente apontando alguns erros de
cálculo ou impressão.
Na verdade, as análises não se restringem
a apontar acertos e eventuais defeitos encontrados nos 36 textos
estudados. Críticas são feitas e são muitas. Mas se baseiam em princípios
claramente enunciados, muitos deles delineados na Introdução que abre o livro. E
são sempre seguidas de orientação, sugestões e até mesmo exemplos, ilustrando o
caminho a seguir.
Por isso, Exame de Textos é um
livro que educa, abre horizontes, apresenta desafios e ensina a ensinar. Tem
tudo para tornar-se um clássico, leitura obrigatória para quem gosta de
Matemática e de ensiná-la.
Transcrevemos a seguir o Posfácio
do livro, que, nas palavras do Professor Elon Lages Lima, “resume a impressão
que me restou após a leitura de tantos volumes, acompanhada de freqüentes
discussões com meus sete co-autores”.
Elon Lages Lima
IMPA, RJ
Ao concluirmos este trabalho, temos plena
consciência de que não examinamos todos os livros adotados em nosso Ensino
Médio, mesmo porque a cada ano surgem novos títulos, enquanto outros saem de
circulação. Isso, sem mencionar as inúmeras apostilas, às vezes anônimas e
freqüentemente mal concebidas, que tantas escolas utilizam. Por outro lado,
estamos certos de que as coleções aqui analisadas são adotadas pela absoluta
maioria dos professores. Mais ainda: elas refletem em seu bojo a atitude, a
visão da matéria, a linguagem, os hábitos e o conhecimento matemático
predominantes no meio em que estão inseridas.
Por isso não hesitamos em considerar a
amostra da qual dispomos representativa o suficiente para permitir, a partir
dela, falar genericamente, sem mencionarmos as exceções de praxe, caso existam.
O livro didático é o instrumento essencial
utilizado pelo professor para realizar o seu trabalho. Dele são tiradas as
listas de exercícios, é nele que estão as definições, os exemplos, as
observações, as demonstrações e a linguagem a ser usada na comunicação com a
classe. Muitas vezes (quase sempre) o livro didático é onde o professor aprende
aquilo que vai transmitir a seus alunos, pois em geral não estudou na faculdade
(se é que freqüentou alguma) um número considerável de assuntos que fazem parte
do currículo escolar.
Portanto, o nível, a qualidade do ensino
e, conseqüentemente, a formação adquirida pelo aluno dificilmente serão
superiores ao nível e à qualidade média dos livros didáticos disponíveis. Daí a
importância dos mesmos.
Da extensa leitura que fizemos, refletida
nos comentários das páginas precedentes, emerge a figura do livro genérico
brasileiro de Matemática para o Ensino Médio.
O livro genérico não é nenhum dos que
existam realmente. Entretanto, cada uma de suas características, que
enumeraremos a seguir, está presente na maioria (pelo menos oitenta por cento)
dos textos atualmente em uso. E, reciprocamente, esses compêndios possuem a
maioria (ainda oitenta por cento, pelo menos) das características do livro
genérico.
E quais são essas qualidades e defeitos do
livro genérico?
Ele é muito bem impresso e diagramado, em
várias cores, com belas ilustrações, embora as figuras matemáticas contenham
muitas imprecisões e erros.
Seu texto não induz o leitor (aluno) a
pensar. Quando propõe problemas que exigem raciocínio, são quebra-cabeças que
não se relacionam com a matéria ensinada.
Transmite sistematicamente a impressão de
que as conclusões gerais da Matemática resultam do exame superficial de dois ou
três casos particulares.
Contém afirmações gerais obviamente
falsas, que poderiam ser evitadas mediante cuidados elementares, como no uso
indevido da Regra de Cramer.
Usa uma terminologia peculiar, que o aluno
deverá esquecer em estudos posteriores, na Universidade. Exemplos: ciclo
trigonométrico, paralelas coincidentes, retas ortogonais devem ser reversas,
interceptar em vez de intersectar, função afim não pode ser constante.
Omite inteiramente qualquer menção a um
dos conceitos mais relevantes da Matemática, que é o de vetor, cujo uso
simplificaria e esclareceria enormemente o estudo dos sistemas lineares.
Não estabelece conexões entre os assuntos
estudados em diferentes capítulos ou volumes. Exemplo: progressão geométrica e
função exponencial.
Das três componentes básicas do ensino da
Matemática (conceituação, manipulação, aplicações), privilegia a manipulação. A
parte conceitual é extremamente deficiente e as aplicações reais,
contextualizando os temas estudados, praticamente inexistem.
Tomemos quatorze assuntos dentre os mais
relevantes que se estudam no Ensino Médio e vejamos rapidamente como o livro
genérico os trata.
1.
Conjuntos e funções. Não fica claro para o leitor (aluno ou
professor) que os conjuntos são o modelo matemático para o raciocínio lógico.
(Por exemplo: que a implicação lógica eqüivale a uma inclusão entre conjuntos.)
Funções são definidas como relações binárias, ponto de vista que nenhum
matemático nem usuário da Matemática adota em seu dia-a-dia. Pior: esta
generalidade inútil é rapidamente abandonada e todas as funções que surgem
depois são bolinhas e flechinhas, ou então dadas por fórmulas.
2.
Números reais. Apresentação obscura. Não há menção a medidas.
Deseduca e mistifica. Exemplo:
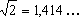 é irracional porque não é uma decimal periódica. Quem
garante isso? Ou então: é irracional porque não é uma decimal periódica. Quem
garante isso? Ou então:
 quando b está à direita de a na reta. Como
saber se quando b está à direita de a na reta. Como
saber se
 ou não? ou não?
3.
Função afim. A importantíssima noção de proporcionalidade, que
o aluno não aprendeu corretamente no Ensino Fundamental, não é retomada de forma
adequada. A caracterização da função afim (acréscimos iguais a x
provocam acréscimos iguais em
 ) nunca é mencionada. Que seu gráfico é uma reta é uma
conclusão nunca provada, mas afirmada a partir de três pontos particulares num
exemplo particular. Além disso, é chamada função do primeiro grau, como se
funções tivessem graus. ) nunca é mencionada. Que seu gráfico é uma reta é uma
conclusão nunca provada, mas afirmada a partir de três pontos particulares num
exemplo particular. Além disso, é chamada função do primeiro grau, como se
funções tivessem graus.
4.
Função quadrática. Um acúmulo de impropriedades. O método de
completar quadrados, instrumento essencial para o estudo deste tópico, não é
usado nem ao menos mencionado. A forma canônica do trinômio, idem. A parábola
não é definida geometricamente nem é feita a conexão com a curva de mesmo nome
(a mesma curva) estudada na terceira série. Os inúmeros e interessantes
problemas contextuais que o assunto permite (e que livros didáticos já expunham
há 250 anos) se reduzem a um único. Empregos importantes da parábola, como
antenas de televisão, por exemplo, não são mencionados.
5.
Funções exponenciais e logarítmicas. São tratadas
separadamente e só de passagem é dito que uma é a inversa da outra. Há menção,
extremamente anacrônica, de tábuas de logaritmos e pouco uso da calculadora. Os
variados, atuais e importantes exemplos em que estas funções são aplicadas são
escassos e apresentados sob a forma enganosa em que a exponencial e o logaritmo
já vêm junto com o enunciado do problema. As propriedades características
destas funções não são mencionadas, logo não é possível propor questões em que
elas sejam usadas na resolução mas não ocorram no enunciado. Nunca é observado
que progressões geométricas são discretizações de funções exponenciais.
6.
Trigonometria. Tratamento
demasiadamente longo, com ênfase em trivialidades, omissões importantes,
conceitos mal definidos e ausência de problemas contextuais atraentes. O radiano
é mal definido, as calculadoras não são enfatizadas e nunca é claramente exposta
a diferença entre o seno (por exemplo) de um ângulo e o seno de um número.
7.
Progressões aritméticas e geométricas. A noção de seqüência é
definida incorretamente. Uma P.A. não é exibida geometricamente como pontos
igualmente espaçados sobre uma reta nem como pontos situados sobre uma reta do
plano cartesiano (o que deixaria claro que uma P.A. é a discretização de uma
função afim). A soma dos termos de uma P.A. finita não é relacionada com uma
função quadrática nem são mencionadas P.A.’s de segunda ordem. Não é feita a
conexão entre P.G. e função exponencial nem são oferecidos problemas não
artificiais que exibam situações de fato onde se poderiam usar P.G.’s ou funções
exponenciais. Temas irrelevantes e inúteis como produto dos termos de uma P.G.
são destacados. Na soma dos termos de uma P.G. infinita, nenhuma explicação é
dada sobre o fato de que
 quando quando
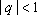 . A Matemática Financeira não é suficientemente
desenvolvida. . A Matemática Financeira não é suficientemente
desenvolvida.
8.
Análise Combinatória. O livro genérico deixa a impressão de
que os problemas combinatórios se reduzem à questão de saber se se trata de uma
permutação, uma combinação ou um arranjo e então aplicar a fórmula, sem se dar
conta de que a maioria dos problemas interessantes de contagem não cabe nesse
restrito formato. Não são propostas questões nas quais o leitor tenha que tomar
decisões a partir da contagem de situações.
9.
Álgebra Linear. Enquadramos sob esta epígrafe os capítulos de
matrizes, determinantes e sistemas lineares. O tratamento deste tópico no livro
genérico é provavelmente o mais anacrônico e mal concebido de todo o programa de
Matemática do Ensino Médio. A noção de vetor que, como dito acima, seria o
elemento unificador, esclarecedor e simplificador, não é mencionada, embora
esteja presente nas linhas e colunas das matrizes e nas soluções dos sistemas.
Os conceitos de combinação e dependência
linear também não são mencionados, embora indispensáveis para explicar os fatos
e enunciar as conclusões. Com efeito, uma matriz é invertível se, e somente se,
nenhuma de suas linhas (ou colunas) é combinação linear das outras. Um sistema
linear possui solução se, e somente se, a coluna dos termos independentes é
combinação linear das colunas da matriz do sistema. Um determinante se anula
quando, e somente quando, uma de suas linhas (ou colunas) é combinação linear
das demais. Esta injustificável omissão evidencia falta de preparo de nossos
autores.
Mesmo sem falar nas omissões acima citadas
(porém como conseqüência delas), há falhas imperdoáveis no tratamento da Álgebra
Linear dado no livro genérico. O estudo de matrizes é desmotivado, com
definições arbitrárias e afirmações peremptórias não justificadas. Determinantes
são incorretamente definidos e suas propriedades fundamentais não são
devidamente destacadas. Dessas propriedades elementares (segundo as quais o
determinante é uma função multilinear alternada das linhas ou colunas da
matriz), resultaria facilmente que o determinante do produto de duas matrizes é
o produto dos seus determinantes. Este fato é citado, mas nunca é provado.
No estudo de sistemas lineares, a Regra de
Cramer é destacada como um método de resolução sem que se perceba que
dificilmente método menos eficiente pode existir. Também a inversão de matrizes
é proposta, sem que se dê conta de que inverter uma matriz
 requer resolver n sistemas lineares requer resolver n sistemas lineares
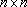 . .
Há muito mais o que criticar no lamentável
tratamento dado em nosso ensino a um tópico de tão grande importância como a
Álgebra Linear. Mas encerremos este assunto dizendo que uma visão geométrica dos
sistemas
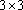 , nunca apresentada, muito ajudaria o entendimento do
assunto. E que o tema permite aplicações bastante interessantes, como os
tradicionais problemas de ligas e vários outros mais modernos, os quais não são
estudados. , nunca apresentada, muito ajudaria o entendimento do
assunto. E que o tema permite aplicações bastante interessantes, como os
tradicionais problemas de ligas e vários outros mais modernos, os quais não são
estudados.
10. Geometria
Espacial. A Geometria é tratada de modo insatisfatório no livro
genérico. A escolha dos axiomas é no mínimo curiosa. É dada ênfase ao chamado
“axioma fundamental”, segundo o qual a reta, o plano e o espaço têm infinitos
pontos. Este axioma nunca é usado. Como o ponto médio de um segmento tem sua
existência admitida sem discussão, bastaria dizer que a reta não se reduz a um
só ponto para garantir que há infinitos pontos na reta. Além disso, na primeira
série admite-se uma bijeção entre IR
e a reta, logo esta é infinita. Quanto ao plano, bastaria dizer que há nele três
pontos não colineares. E que no espaço há quatro pontos não coplanares. Em todo
o livro genérico, os autores mostram muito pouca familiaridade com a Geometria e
com o método dedutivo em geral. Há uma grande pressa de passar do desordenado
tratamento da geometria da posição para o estudo de áreas e volumes,
predominantemente aritmético.
O volume de um sólido nunca é definido,
nem sequer intuitivamente. A fórmula do volume do bloco retangular é “deduzida”
a partir de um exemplo particular onde as arestas têm medidas inteiras. As
demais baseiam-se em argumentos mal explicados e omissões de pontos
essenciais. O Teorema de Euler para poliedros é demonstrado incorretamente.
Incorreta também é a definição de poliedro.
11. Geometria
Analítica. A falta de objetividade e de autocrítica na feitura do
livro genérico fica patente aqui. A condição de alinhamento de três pontos e a
equação de uma reta são apresentadas sob a forma de um determinante
 , o que é um opção infeliz. Nunca é observado que a reta de
equação , o que é um opção infeliz. Nunca é observado que a reta de
equação
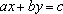 (ou (ou
 , como o livro genérico inadequadamente prefere) é
perpendicular ao segmento AO, onde , como o livro genérico inadequadamente prefere) é
perpendicular ao segmento AO, onde
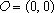 e e
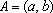 . Isto tornaria imediata a obtenção da fórmula da distância
de um ponto a uma reta. Não são apresentados os numerosos e eloqüentes exemplos
de uso da Geometria Analítica para resolver problemas de Geometria Plana. As
seções cônicas são estudadas apressadamente, sem que se discutam suas várias
aplicações nem que suas equações sejam deduzidas corretamente. Mais uma vez
falta o método de completar quadrados. Também fazem falta os vetores. Outro
ponto inexplicável é a ausência das coordenadas no espaço. Pelo menos a equação
do plano permitiria interpretar geometricamente um sistema linear . Isto tornaria imediata a obtenção da fórmula da distância
de um ponto a uma reta. Não são apresentados os numerosos e eloqüentes exemplos
de uso da Geometria Analítica para resolver problemas de Geometria Plana. As
seções cônicas são estudadas apressadamente, sem que se discutam suas várias
aplicações nem que suas equações sejam deduzidas corretamente. Mais uma vez
falta o método de completar quadrados. Também fazem falta os vetores. Outro
ponto inexplicável é a ausência das coordenadas no espaço. Pelo menos a equação
do plano permitiria interpretar geometricamente um sistema linear
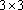 . .
12. Números
Complexos. A aritmética dos números complexos não apresenta
dificuldades. A conexão com a Geometria, porém, é deficiente, o que é estranho,
pois a Geometria Analítica acabou de ser estudada. É mais um exemplo de falta de
conexão entre os capítulos. As aplicações geométricas das operações entre
complexos (principalmente a multiplicação), tão belas como variadas, não são
exploradas. Isto é imperdoável, pois todo matemático ou usuário da Matemática,
ao pensar num número complexo, sempre o imagina como um ponto do plano
coordenado e as operações são interpretadas como transformações geométricas.
13. Polinômios.
O livro genérico não traz gráficos de polinômios de grau superior a 2. Não traz
exemplos de problemas contextuais que requeiram a resolução de uma equação de
grau superior a 2. Não deixa claro ao leitor que as fórmulas que expressam as
raízes das equações do terceiro e quarto graus são inúteis e que os métodos
numéricos (como o de Newton) são eficientes e estão ao alcance dos alunos,
principalmente com uma boa calculadora ou um computador.
14.
Cálculo. Em algumas edições, o
livro genérico traz capítulos sobre Cálculo Diferencial. Seria melhor não
trazê-los. Os alunos vão estudar o assunto na universidade e os que não vão ao
terceiro grau não aprenderão aqui nada que se aproveite.
|