Painel I:
A regra dos 70
Antonio Carlos Gilli Martins
IMECC, Unicamp,
SP
|
 |
Dias atrás presenciei uma conversa na qual
um cliente perguntava, ao gerente de um banco, quanto tempo levaria para
duplicar uma quantia a ser aplicada a uma taxa de i%

Eu, muito curioso, pedi ao gerente uma
explicação para o cálculo e ele me disse que “era uma regra usada em
finanças conhecida como a regra dos 70”. O porquê do 70 ele não sabia, mas
dava certo.
Para calcular o tempo aproximado de
duplicação de um investimento,
divida 70 pela taxa percentual anual de juros.
Vamos justificar o cálculo do gerente. Para
isso, usaremos a função logaritmo natural de
x,x>0, denotada por
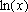 , que pode ser definida como sendo a função inversa da
exponencial , que pode ser definida como sendo a função inversa da
exponencial
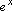 . Logo, . Logo,
“o logaritmo natural de x é a
potência de e necessária para se obter x.”
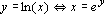 . .
Precisamos de uma forma prática para
calcular o valor numérico do logaritmo, mesmo que aproximado. Usaremos a
expressão apresentada, com notas históricas, na
RPM 26, pág. 6, que é a seguinte:
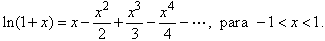
Tal expressão, conhecida como a série de
Taylor da função
 , permite a aproximação , permite a aproximação
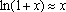 para valores de x positivos e próximos de 0. para valores de x positivos e próximos de 0.
Podemos também perceber essa aproximação
graficamente:
Voltemos à regra dos 70.
Um capital C, aplicado à taxa anual
de
 % transforma-se, após 1 ano, em % transforma-se, após 1 ano, em

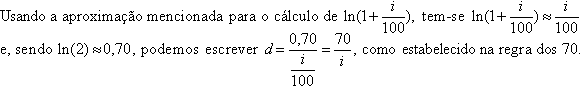

A regra também vale para estimar a meia-vida
de uma quantidade Q que decai exponencialmente com taxa de
decrescimento de i% ao ano. Após t anos, o valor da
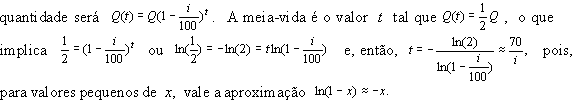
Painel II:
Polinômios gerando
primos
Wilson Carlos da Silva Ramos
Belém, PA
|
|
Os primos aparecem com muita irregularidade
na seqüência dos números inteiros, e por isso foram criadas muitas fórmulas
que fornecem números primos.
Há certos polinômios
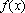 , com coeficientes inteiros, cujos valores numéricos são
primos para valores inteiros da variável x. Vejamos alguns: , com coeficientes inteiros, cujos valores numéricos são
primos para valores inteiros da variável x. Vejamos alguns:
1)
Os valores assumidos por
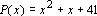 (trinômio de Euler) são primos para (trinômio de Euler) são primos para
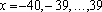 (observe que (observe que
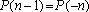 ). Entretanto, para ). Entretanto, para
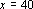 e e
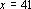 , os valores numéricos desse trinômio não são primos,
pois, temos: , os valores numéricos desse trinômio não são primos,
pois, temos:
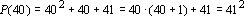
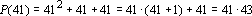
Para
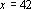 , temos , temos
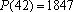 , um primo, mas não se sabe se o trinômio de Euler
produz um número infinito de primos para valores inteiros de x. , um primo, mas não se sabe se o trinômio de Euler
produz um número infinito de primos para valores inteiros de x.
2)
Outro trinômio campeão de
primos é Q(x) = P(x
 40) = x2
40) = x2
 79x + 1601. Para x=0,1,2,...,79 , Q fornece números primos (ver
RPM 09, pág. 33).
79x + 1601. Para x=0,1,2,...,79 , Q fornece números primos (ver
RPM 09, pág. 33).
3)
O binômio de Legendre P(x)
= 2x2 + 29 produz primos para x= 28, 28, 27,...,28. 27,...,28.
4)
P(x) = x2
 2999x
+ 2248541 produz primos para x=1460,...,1539. 2999x
+ 2248541 produz primos para x=1460,...,1539.
5)
P(x) = x2
+ x + 17 produz primos para x= 15, 15, 14,...,15. 14,...,15.
6)
P(x) = 3x2
+ 3x + 23 produz primos para
x= 21, 21, 20,...,21. 20,...,21.
7)
P(x) = 6x2
+ 6x + 31 produz primos para x= 29, 29, 28,...,28. 28,...,28.
Agora façamos a seguinte pergunta: existirá
algum polinômio P(x) , com coeficientes inteiros, cujos valores numéricos são
sempre números primos para valores inteiros da variável x?
A resposta é
não, e é conseqüência do seguinte teorema:
Teorema:
Não existe polinômio algum, com coeficientes inteiros, cujos valores
numéricos são sempre números primos para valores inteiros da variável x.
Demonstração:
Suponhamos que o polinômio P(x)
= akxk + ak-1xk-1
+ ... + a2x2 + a1x
+ a0, com os coeficientes ak, ak-1,...,
a2, a1, a0 todos inteiros e ak
 0, produz sempre primos para valores inteiros da variável
x. Então, para x = n , sendo n um inteiro fixo, P(x)=p é primo, e qualquer que seja o inteiro t,
temos:
0, produz sempre primos para valores inteiros da variável
x. Então, para x = n , sendo n um inteiro fixo, P(x)=p é primo, e qualquer que seja o inteiro t,
temos:
P(n + pf) = ak(n
+ pf)k + ak-1(n + pf)k-1
+ ... + a1(n + pf) + a0, ou seja, P(n+pf)=(aknk+ak-1nk-1+
... +a2n2=a1n=a0)+pg(t)
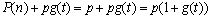 , ,
sendo g(t) um polinômio em t com coeficientes inteiros.
Portanto, p é um divisor de P(n
+ pt) e P(n + pt) é um inteiro composto, a não ser que: P(n+pt)= p ou P(a+pt)=0.
p ou P(a+pt)=0.
Como um polinômio do grau k não
pode assumir o mesmo valor numérico para mais de k valores
numéricos da sua variável, segue-se que as três igualdades anteriores podem
subsistir somente para 3k valores do inteiro t, quando
muito, de modo que, para todos os demais valores de t, P(n
+ pt) é um inteiro composto, o que é uma contradição, visto que o
polinômio
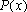 produz sempre primos para valores inteiros da variável
x. produz sempre primos para valores inteiros da variável
x.
Assim, por exemplo, com P(x)=x2+2x+3,
para x=2 temos P(2)=11,
um primo, e P(2+11t)=11(1+6t+11t2) é um inteiro composto, divisível por 11, para todo t 0.
0. |