|
|
|
|
|||
|
|
|||||
|
|
|
|
|||
|
|
|||||
José Paulo Q.
Carneiro
|
|
Introdução |
Quando se procuram valores aproximados
para a raiz quadrada de um número positivo, em geral se pensa em dar esses
valores na forma decimal. Aliás, é assim que eles aparecem em uma calculadora,
por exemplo. Isso é equivalente a exigir que o número racional utilizado como
aproximação tenha como denominador uma potência
de 10. No entanto, os antigos gregos, que nem sequer tinham a notação decimal,
sentiam-se satisfeitos com qualquer outro denominador.
Quando Arquimedes (287-212 a.C.), em seu notável
livro A medida do círculo, aproxima o
comprimento da circunferência por meio dos
perímetros de polígonos regulares inscritos e
circunscritos, usa, sem dar nenhuma explicação,
valores aproximados para ![]() , tais como 265/153 e 1.351/780. Observamos que
, tais como 265/153 e 1.351/780. Observamos que
![]() e
e ![]() . Os estudiosos têm especulado sobre o método pelo qual os
gregos teriam chegado a essas aproximações (ver [6]). À primeira vista, parece
que elas provêm das frações contínuas (ver [8] e [3]).
. Os estudiosos têm especulado sobre o método pelo qual os
gregos teriam chegado a essas aproximações (ver [6]). À primeira vista, parece
que elas provêm das frações contínuas (ver [8] e [3]).
|
De fato, a fração contínua simples
para |
|
(repetindo-se indefinidamente o padrão 1,
2, 1, 2, ...), produz as seguintes aproximações para
![]() :
:
1
![]()
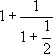
 ...
...
isto é:
1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ...
...
As seis primeiras decimais (não utilizadas naquela época) de cada fração são, respectivamente:
1,000000 2,000000 1,666667 1,750000 1,727273 1,733333 1,731707 1,732143 1,732026 1,732057 1,732049 1,732051 ...
Pode-se observar que as aproximações são
alternadamente por falta e por excesso (ver [8]), e que as aproximações usadas
por Arquimedes estão nessa lista. Entretanto, é estranho que Arquimedes tivesse
em mente essa lista, pois por que teria ele utilizado o 9o e o
12o termos da lista, e não dois consecutivos, como parece mais
natural? Além disso, alguns historiadores objetam que a teoria das frações
contínuas só teria surgido cerca de 18 séculos depois de Arquimedes, com os
italianos Bombelli (1526-1573?) e, principalmente, Cataldi (1548-1626). Essa
objeção, porém, não é séria, pois vestígios de uso de frações contínuas aparecem
em vários autores da antigüidade, e, além disso, o próprio algoritmo de Euclides
(300 a.C.) para o MDC identifica-se essencialmente com a fração contínua para um
número racional (ver [9]).
 contínuas. Um
esquema desse tipo para
contínuas. Um
esquema desse tipo para ![]() é mencionado por Thurnbull ([5]), que o chama de “escada de
Eudoxo” (matemático ateniense que viveu de 408 a 355 a.C.).
é mencionado por Thurnbull ([5]), que o chama de “escada de
Eudoxo” (matemático ateniense que viveu de 408 a 355 a.C.).
É provável que, já na época de Arquimedes, circulassem listas de aproximações racionais para raízes quadradas, obtidas por diversos métodos. Um desses métodos, que nos parece particularmente atraente, e preserva seu interesse ainda hoje, é o uso de médias. Esse processo já era conhecido pelo matemático grego Herão de Alexandria (100 d.C.), e é atribuído por alguns a Arquitas de Taranto (428-365 a.C.). Mas, na primeira metade do século XX, descobriu-se que ele já era utilizado pelos mesopotâmios (onde hoje é o Iraque), há uns 3500 anos (ver [1]).
|
Médias |
Recordemos que, dados dois números positivos a e b, suas médias aritmética A, geométrica G, e harmônica H têm as propriedades:
![]()
(ii) ![]()
A demonstração dessas propriedades é
simples (ver [7]), e as idéias básicas são as seguintes: Como
![]() , segue imediatamente que
, segue imediatamente que
![]() , e que a igualdade só ocorre quando
, e que a igualdade só ocorre quando
![]() . Aplicando-se esse mesmo resultado a
. Aplicando-se esse mesmo resultado a
![]() e a
e a ![]() ,
,
![]()
do cálculo direto. É conveniente observar, para uso na sala de aula, que essas
propriedades têm interpretações geométricas muito sugestivas, algumas delas
encontradas em [5].
|
Utilização de médias para aproximar raízes quadradas |
Vamos usar esses fatos para calcular, por
exemplo, aproximações racionais de
![]() . Primeiro, como
. Primeiro, como
![]() , temos, pela propriedade (i):
, temos, pela propriedade (i):
![]()
![]()
![]() .
.
Como, pela propriedade (ii), a média
geométrica dessas duas novas frações continua sendo igual a
![]() , temos:
, temos:

Aplicando sucessivamente o mesmo procedimento:
![]()
![]()
![]() ,
, ![]()
![]()
![]()
(Você observa algum parentesco entre essa lista de aproximações e a anterior, obtida por frações contínuas?)
|
Em decimais, as aproximações agora obtidas são, aproximadamente: |
|
O último valor já é uma aproximação excepcional, e sua precisão pode ser observada na curiosa desigualdade:
![]()
|
O procedimento geral |
Generalizando, o processo consiste no
seguinte: dado um número ![]() , do qual se quer calcular a raiz quadrada, fatora-se o
referido número na forma
, do qual se quer calcular a raiz quadrada, fatora-se o
referido número na forma ![]() , com
, com ![]() . Em seguida, formam-se:
. Em seguida, formam-se:
![]()
![]()
![]()
Vamos verificar agora que o processo funciona sempre. Em primeiro lugar, pelas propriedades das médias recordadas no início, tem-se, para todo n:
![]()
![]()
|
Além disso: |
|
![]()
Isto é, os
![]() são aproximações por falta, cada vez melhores, de
são aproximações por falta, cada vez melhores, de
![]() , enquanto os
, enquanto os
![]() são aproximações por excesso, cada vez melhores, de
são aproximações por excesso, cada vez melhores, de
![]() .
.
![]()
Mais ainda, a seqüência crescente formada
pelos ![]() é limitada superiormente por
é limitada superiormente por
![]() (e portanto converge a um número c), enquanto a
seqüência decrescente formada pelos
(e portanto converge a um número c), enquanto a
seqüência decrescente formada pelos
![]() é limitada inferiormente por
é limitada inferiormente por
![]() (e portanto converge a um número d), sendo
(e portanto converge a um número d), sendo
![]() . Porém,
. Porém,
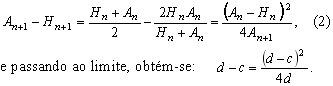
Se
![]() , teríamos
, teríamos
![]() , o
, o ![]() , o que é impossível, com c e d positivos.
Logo,
, o que é impossível, com c e d positivos.
Logo, ![]() .
.
Conclusão: as seqüências de médias
harmônicas e aritméticas obtidas no processo formam aproximações cada vez
melhores de ![]() , por falta e por excesso, respectivamente, e aproximam-se de
, por falta e por excesso, respectivamente, e aproximam-se de
![]() tanto quanto quisermos tomar termos da seqüência em número
suficiente.
tanto quanto quisermos tomar termos da seqüência em número
suficiente.
|
A precisão do processo |
Podemos analisar agora o erro cometido nas aproximações.
Como
![]()
![]() , tanto o erro cometido ao tomar a n-ésima aproximação
por excesso, isto é,
, tanto o erro cometido ao tomar a n-ésima aproximação
por excesso, isto é, ![]() , quanto o erro cometido ao tomar a n-ésima
aproximação por falta, isto é,
, quanto o erro cometido ao tomar a n-ésima
aproximação por falta, isto é,
![]() , são menores que
, são menores que
![]() .
.
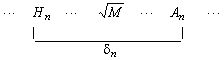
![]()
Sendo u uma aproximação por falta
de ![]() , tem-se que
, tem-se que
![]() , de modo que
, de modo que ![]()
Essa desigualdade permite verificar que o
erro decresce muito rapidamente, a partir do momento em que seja menor que 1, o
que obrigatoriamente termina por ocorrer, já que
![]() tende a zero.
tende a zero.
Por exemplo, suponhamos que se queira
calcular ![]() . Pode-se tomar
. Pode-se tomar
![]() , de modo que
, de modo que
![]() . Isso significa que, se, em alguma etapa do processo,
. Isso significa que, se, em alguma etapa do processo,
![]() for, digamos,
for, digamos,
![]() , então, na etapa seguinte, não excederá a
, então, na etapa seguinte, não excederá a
![]() , na seguinte a
, na seguinte a
![]() , e assim por diante, o que representa uma convergência muito
rápida.
, e assim por diante, o que representa uma convergência muito
rápida.
Não é interessante escolher agora a
fatoração ![]() , pois as primeiras aproximações serão muito pobres:
, pois as primeiras aproximações serão muito pobres:
![]() e
e ![]() , com
, com ![]() e
e ![]() , o que é ridículo.
, o que é ridículo.
Mas se tomarmos a fatoração
![]() , a situação já é muito melhor:
, a situação já é muito melhor:
|
n |
|
|
|
|
|
0 |
6 |
19 |
13 |
4,225 |
|
1 |
|
|
3,38 |
0,285610 |
|
2 |
|
|
0,264209 |
0,001745 |
|
3 |
|
|
0,001634 |
0,000000 |
O último valor, na realidade, não é 0, e
sim 0,00000007, aproximadamente, mas em todo caso mostra que as aproximações
seguintes (por falta e por excesso) vão coincidir até as seis casas decimais que
estamos usando. O leitor poderá comprovar que são iguais a 10,677078, o que
corresponde a ![]() com seis decimais exatas.
com seis decimais exatas.
Como
![]() , vê-se que a convergência será tanto mais rápida quanto mais
próximos estiverem os dois fatores escolhidos inicialmente. Por fim, deve-se
notar que, se o objetivo é obter somente aproximações em decimais, nada impede
que sejam utilizados valores iniciais não inteiros. (Aliás, a utilização de
fatores não inteiros será essencial quando M for primo, e mais ainda
quando M não for inteiro, já que o processo vale para qualquer número
real.) Por exemplo, para
, vê-se que a convergência será tanto mais rápida quanto mais
próximos estiverem os dois fatores escolhidos inicialmente. Por fim, deve-se
notar que, se o objetivo é obter somente aproximações em decimais, nada impede
que sejam utilizados valores iniciais não inteiros. (Aliás, a utilização de
fatores não inteiros será essencial quando M for primo, e mais ainda
quando M não for inteiro, já que o processo vale para qualquer número
real.) Por exemplo, para ![]() pode-se utilizar
pode-se utilizar
![]() e
e ![]() , o que equivale a
, o que equivale a
![]() A convergência será bastante rápida:
A convergência será bastante rápida:
|
n |
|
|
|
|
0 |
10 |
11,4 |
1,4 |
|
1 |
10,654206 |
10,700000 |
0,045794 |
|
2 |
10,677054 |
10,677103 |
0,000049 |
|
3 |
10,677078 |
10,677078 |
0,000000 |
|
Comentários e conclusão |
Se, na relação de recorrência (1), se levar em conta que HnAn = M , obtém-se:
![]() (3)
(3)
Ou seja, cada aproximação por excesso obtida durante o processo é a média aritmética entre a aproximação por excesso anterior An e M/An. De modo inteiramente análogo, o leitor pode comprovar que cada aproximação por falta Hn+1 é a média harmônica entre a aproximação por falta anterior Hn e M/Hn. Isso significa que o processo descrito pela fórmula (3) coincide com o conhecido “método de Newton (1642-1727)” (ver [2], [4] e RPM 21, pág.13).
Mais uma vez se constata que, ao estudar a história da Matemática, o professor pode extrair daí não somente episódios curiosos, mas também questões interessantes, que permitam a seus alunos investigar métodos diferentes dos usuais, e igualmente instrutivos.
[1] BOYER, Carl Boyer. História da Matemática, Editora Edgar Blucher, 1974.
[2] CARNEIRO, José Paulo Q. Resolução de equações algébricas, Editora Universidade Santa Úrsula – 1998.
[3] CARNEIRO, José Paulo Q. Um processo finito para a raiz quadrada, RPM 34, 1997.
[4] CARNEIRO, José Paulo Q. Equações algébricas de grau maior que dois: assunto para o Ensino Médio?, RPM 40, 1999.
[5] HARIK, Seiji. Média harmônica, RPM 32, 1996.
[6] HEATH, T.L. The works of Archimedes, Dover, New York, 1897.
[7] LIMA, Elon Lages. Meu professor de Matemática e outras histórias, SBM, 1993.
[8] MOREIRA, Carlos Gustavo. Frações contínuas, representações de números e aproximações, Eureka, no 3, 1998.
[9] OLDS, C.D. Continued fractions, The Mathematical Association of America, 1963.