Maria Cristina Bonomi Barufi
IME – USP
     Introdução

O presente artigo visa discutir um problema relacionado ao conteúdo desenvolvido nas
didáticos, sendo seu gráfico considerado uma hipérbole sem, entretanto, uma argumentação matemática razoável ou determinação de seus focos.

Consideramos que tal assunto pode ser abordado após o estudo das cônicas – assunto bastante detalhado pela RPM, com a publicação de diversos artigos. Trata-se do estudo de uma função cujo domínio não é o conjunto de todos os reais, sendo necessário excluir um único ponto do conjunto R, para obter seu campo de definição. A generalização para uma função racional, com numerador de grau no máximo 1 e denominador de grau 1, pode ser feita de maneira bastante natural, explorando movimentos no plano. Esse tipo de abordagem parece ser interessante, pois estimula a leitura e interpretação de gráficos e, considerando a questão sob um ponto de vista mais amplo, possibilita estabelecer significado para operações algébricas.

Lembremos que, dados dois pontos   e ,  denominamos hipérbole de focos   e   à curva que é o lugar geométrico dos pontos de um plano por   e ,  tais que

    (*)

onde a constante  2a  é um número positivo dado inicialmente e é a distância entre os vértices da hipérbole, que são os dois pontos da curva, um em cada ramo, tal que a distância entre eles é a menor possível.

cada número real não nulo associa o seu inverso, percebemos que os pontos dos dois ramos do gráfico que estão à distância mínima são A1 = (1, 1)  e, A2 = (1, 1) sendo a distância entre eles .

Para garantir que esse gráfico é uma hipérbole, precisamos encontrar dois pontos   e ,  do plano  xy,  que sejam os focos e mostrar que:

(i)   todo ponto do gráfico da função verifica a propriedade (*);

Busquemos então quais pontos são razoáveis candidatos a focos. Lembrando que os focos de uma hipérbole pertencem à reta que passa pelos seus vértices e são simétricos em relação ao ponto médio do segmento determinado pelos mesmos vértices, teremos que procurar pontos da forma , com  p > 1.

,  logo,  .

Com  , podemos escrever

Efetuando os cálculos necessários, obtemos:

isto é,  ,  de onde concluímos que    ou  ,  ou seja, os pontos   são os candidatos a focos da hipérbole. Podemos verificar também que   .

Vamos provar em seguida o primeiro resultado de uma série de cinco:

Resultado 1: O gráfico de    é uma hipérbole de focos .

Prova do resultado: Devemos mostrar as afirmações (i) e (ii) a seguir.

(ii)    Para todo ponto  (x, y)  tal que

,  temos .

Efetuando os cálculos necessários, obtemos

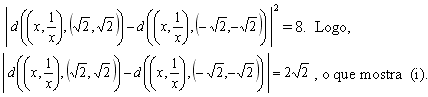
Por outro lado, se  (x, y)  é tal que

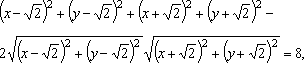
então, efetuando os cálculos, obtemos

,  de onde concluímos que      xy = 1,  o que mostra  (ii).

I.                   Como é o gráfico de, por exemplo, , quando comparado com o gráfico de  ?

Para um mesmo valor não nulo da abcissa, o valor da ordenada na função    é o dobro do valor da ordenada na função  f; logo, ocorre, em relação à função inicial, uma mudança de “inclinação” com a curva se afastando da origem.

Supondo que o gráfico de    também seja uma hipérbole, vejamos qual é a ação do coeficiente  2  nos focos da nova hipérbole em comparação aos focos da primeira hipérbole, gráfico de  f.

Inicialmente, observemos, pela simetria, que os vértices da nova curva são os pontos   (de   )  e a distância entre eles é  4. Em segundo lugar, observemos ser razoável que os novos focos sejam os pontos . De fato, no gráfico da função inicial , os vértices eram os pontos  e os focos

Resultado 2:  O gráfico de , onde  k  é uma constante não nula, é uma hipérbole cujos focos são os pontos   e tal que a distância entre os vértices é igual a .

Observemos que, para um mesmo valor da variável  x,  a ordenada correspondente do ponto no gráfico de    é igual à ordenada do ponto
Assim sendo, não há mudança de “inclinação” na curva, mas ocorrerá alteração nas ordenadas

dos focos, com adição da constante  h.  Esse fato é o Resultado 3, cuja demonstração é novamente análoga à do Resultado 1 e pode ser dispensada se a idéia da translação for clara.

II.  Se efetuarmos uma translação horizontal através da constante  m,  no gráfico de 

 

Nesse caso, não há mudança de “inclinação” no gráfico da nova função, e as abcissas dos focos são alteradas através da adição da constante  m.

Temos assim o seguinte resultado:

       

III.  Finalmente, a situação mais geral, englobando os dois últimos resultados, pode ser colocada na forma:


ocorreu uma translação horizontal através da constante  m,  a seguir uma mudança de “inclinação” através da constante  k  e, finalmente, uma translação vertical através da constante  h.  Podemos, assim, enunciar o resultado seguinte:


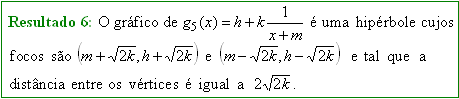
 Assim, de acordo com o Resultado 6, os focos da curva são os pontos

 

 

 

Maria Cristina Bonomi Barufi é licenciada e mestre em Matemática pelo IME, USP, doutora em Didática pela FE, USP, docente do IME, USP, e membro da diretoria do CAEM, Centro de Aperfeiçoamento do Ensino de Matemática da USP.