Chegamos ao ano 2000 e um desafio lançado a uma década atrás, na RPM 15, pág. 67, agora pode ser respondido.

A cronologia da história começa em 1984, na RPM 5, pág. 48, onde saiu o “probleminha” de escrever os inteiros de 0 a 25 usando apenas sinais de operação e os algarismos  1, 9, 8 e 4,  na ordem.

Muitas pessoas que gostam de passatempos numéricos se entretiveram com esse probleminha.

Eduardo I. Nunes mandou na RPM 6, pág. 63, soluções para os números de 0 a 100, e para o ano novo 1, 9, 8, 5 fez do 0 ao 50, só não conseguindo o 41. Na RPM 8, pág. 60, João de Deus Lima enviou  41 = 1⁹ + 8 ^. 5   e tentou todos de 0 até 100, não conseguindo do 98 ao 100.

Então, na RPM 9, pág. 66, enviamos o 99 = 19,8 ^. 5 e   com 14 radicais, e uma solução geral para todos os inteiros positivos e para toda a década 198a.

A diversão continuou (RPM 10, pág. 67, RPM 14, pág. 71) até que na RPM 15, pág. 67, enviamos uma outra solução geral para a nova década de 199a, ocasião na qual a RPM agradeceu a colaboração dos leitores e deixou sua despedida até o próximo século, acreditando que essa tradição acabaria no ano 2000.

A década se passou, outras soluções apareceram (RPM 16, pág. 68, RPM 18, pág. 69, RPM 20, pág. 62, RPM 21, pág. 57) e agora com o novo milênio, chegou a hora de se mostrar uma solução para 2, a, b e c:

Qualquer inteiro positivo  n  da forma  pode ser representado por

com  n  radicais.

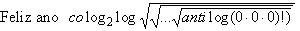
Sérgio Dalmas