Adilson Simonis
Claudio Possani
IME-USP

Os Parâmetros Curriculares Nacionais (PCNs) preconizam que se aborde, desde o ensino fundamental, noções básicas de Estatística. Pretende-se que o estudante seja confrontado com situações concretas de análise de dados através de gráficos ou tabelas, introduzindo conceitos fundamentais para a compreensão dos fenômenos do dia-a-dia. Entre esses conceitos, um de vital importância é a média de uma seqüência de valores numéricos. Nosso objetivo neste artigo é pontuar alguns aspectos desse conceito que possam ser úteis ao professor de Matemática.

Existem várias noções de médias: aritmética, geométrica, harmônica, simétrica, etc. Vamos nos ocupar, neste artigo, da média aritmética, que passamos a denominar apenas média.

Dados os números  x₁, x₂, ... ,x_n   (não necessariamente distintos), a média desses

Uma dúvida muito freqüente acerca das médias é a seguinte: se temos duas seqüências de números A₁ e A₂  com médias  m₁  e  m₂,  respectivamente, e queremos obter a média da união dessas seqüências, é correto fazer  ( + )/2   ou devemos somar todos os números e dividir pelo número total de valores? Esses dois procedimentos levam ao mesmo resultado? Vejamos através de um exemplo que os resultados podem ser diferentes.

Suponha que um professor peça a cada um de seus alunos que calcule a idade média de sua própria família, e imaginemos a seguinte situação:

A idade média da família de   A   é   = (40 + 37 + 13)/3 = 30   anos, e da família de  B é  = (39 + 40 + 12 + 10 + 9)/5 = 22  anos.

Observemos agora os valores:

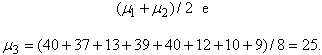
Primeiramente salientamos que não cabe dizer que um procedimento é mais correto que o outro. Cada um deles tem um significado diferente e é correto no contexto adequado.

O valor  26  é a média das idades médias das famílias. Assim, se estivermos interessados em saber se as famílias de uma cidade ou do Brasil são famílias jovens ou não, esse é o tipo de valor que devemos calcular.

Por outro lado, se calculamos a soma total dividida pelo número total de pessoas  ( ),  obtemos a idade média do total de pessoas (e não de famílias). É o que fazemos para obter a idade média da população de uma cidade ou país.

Um outro exemplo no qual os dois procedimentos apresentam resultados diferentes é :

Seqüência 1 de dados:  10, 10, 10, 10, 10, 10, 10, 10.   .

Seqüência 2 de dados: 5, 5.   .

     e     

.

Ao calcular  7,5,  os dois valores,  10  e  5,  aparecem com o mesmo peso, enquanto o cálculo de    reflete o fato de o valor  10  aparecer mais vezes na primeira seqüência do que o valor  5  aparece na segunda.

É fácil ver que, se duas seqüências numéricas,    e  ,  têm o mesmo número de elementos, então os dois procedimentos descritos anteriormente fornecem valores iguais. De fato, sejam    e  . 

Então

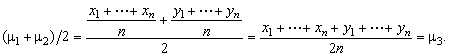
Vamos mostrar agora como se procede para avaliar a média quando não são conhecidos todos os elementos da seqüência numérica.

Em um determinado conjunto ou seqüência de valores numéricos, dois parâmetros são de especial interesse. Ambos são médias e podem surpreender pela quantidade de informação que podemos obter a partir deles sobre a totalidade dos valores numéricos que temos. O primeiro é a média, e o segundo a variância, definida como sendo a média dos quadrados das diferenças entre cada valor e a média.

Vamos exemplificar esses dois conceitos. Considere a seguinte seqüência numérica que denotamos por  :

A média é dada pelo valor 6. Essa quantidade expressa um certo centro de gravidade da seqüência, mas certamente nos informa muito pouco sobre como a seqüência é formada. Se você sabe que a seqüência numérica não é constante, pode apostar que existem valores menores e maiores, centrados em  6,  mas não pode dizer muito mais do que isso, embora saber que a média dos salários dos políticos brasileiros é alta possa ajudar a entender por que existem tantos candidatos a determinado cargo público.

Se a seqüência    representa o salário (em salários mínimos) de  5  professores de Matemática, e considerando que dois ou três salários mínimos não representam um bom salário, você tem que  3  dentre os  5 ganham mal e abaixo da média. Como tentar incorporar essa variabilidade em relação ao valor médio?

É o conceito de variância, denotada por  ,  que tenta expressar a dispersão dos valores em torno da média. O valor  2  (do professor com o salário mais modesto) tem uma distância a  ,  ao quadrado, dada por  (2 6)² = 16 ,  enquanto o valor  12  (o marajá do grupo) tem a distância ao quadrado de   dada por  (12 6)² = 36 .  Fazendo a média de todas as distâncias ao quadrado, encontramos

Como essa distância média fornece os valores dos quadrados dos salários, é usual retornar ao velho, estável e bom salário mínimo tomando a raiz quadrada, e teremos então o valor conhecido como desvio padrão.

O que significa o desvio padrão dado no exemplo por  ? A resposta informal que daremos aqui ficará interessante se imaginarmos um conjunto com centenas de valores (os salários dos professores de Matemática no Brasil, por exemplo) e não apenas os cinco do nosso exemplo. Temos que o valor médio das diferenças, em módulo, entre os valores e sua média é dado por     

O desvio padrão  s  possui uma interpretação muito próxima do valor  obtido acima  (4)  e expressa a idéia de concentração ou não em torno da média. A escolha de  s  tem vantagens computacionais em relação à média dos módulos e talvez por isso o seu uso seja muito difundido.

O intervalo  ,  que no nosso exemplo exclui apenas o marajá, é amplamente utilizado em estatística aplicada quando o conjunto de valores é grande, e podemos argumentar (num próximo artigo?) que nesse caso contempla aproximadamente  70%  das observações, enquanto o intervalo    contempla aproximadamente  99%  das observações.

Podemos considerar o desvio padrão discutido como uma medida de dispersão dos dados, isto é, quanto menor  ,  mais concentrados em torno da média estão as observações. Quando os jornais afirmam que a distribuição de renda dos trabalhadores brasileiros (e não apenas dos professores) é injusta, no fundo, afirmam que a variância é grande. Muitos pobres (professores?) e poucos ricos (políticos?). Por outro lado, se  ,  teríamos tudo igual e, como disse Nélson Rodrigues, a unanimidade é burra.

Discutidos os parâmetros    e  ,  e esperando tê-los convencido da importância destes no entendimento dos dados, vamos ver agora como os estatísticos fazem para estimar essas quantidades em uma seqüência    muito grande, quando observam apenas uma pequena parte desse total. Ou seja, observando apenas alguns valores de  ,  vamos introduzir um particular “chute” para as quantidades    e    que possui qualidades baseadas nas idéias discutidas aqui. Os estatísticos, em média, sabem o que fazem K   Vamos ver informalmente como.

Suponha, que dos cinco salários de professores, você conheça apenas dois valores, digamos  ,  escolhidos de maneira eqüiprovável, dentre os valores que compõem  . Como podemos chutar um valor para  ?  Uma possibilidade é calcular a média (amostral) definida por
 

.

Aqui, não acertamos, pois  ,  mas afirmamos que em média iremos acertar, isto é, a média de    é  .  Vejamos.

Consideremos o conjunto  A  formado pelos professores cujos salários compõem a seqüência  ,  digamos  .  Tomamos o produto cartesiano    e para cada um dos  25  elementos de    calculamos a média    do par de salários dos professores escolhidos.

Assim, as  25  escolhas possíveis para o par    e os respectivos  valores para    são:

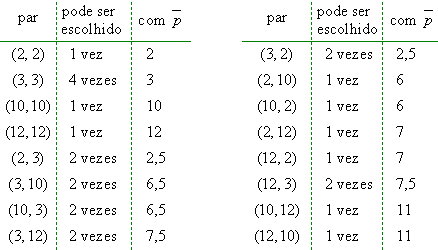
Então a média dos    é calculada por:

Portanto, em média, o chute deu certo!

Isso é um fato geral, isto é, pode ser demonstrado que a média das médias (amostrais) calculadas como acima é a média da seqüência original de valores.

Poderíamos então determinar um intervalo de estimação para    baseado em    (veja RPM 40, págs. 23-28). Para os mais interessados, verifique que a média de

Isso deve explicar por que os estatísticos usam o desvio padrão (amostral) com denominador  ,  em vez de dividir por  n,  como seria de esperar, já que nada mais é que uma outra média... Eles querem acertar em média, como agora sabemos...  

 

Claudio Possani é professor doutor do Departamento de Matemática do IME - USP, atua na pró-reitoria de graduação e além da Matemática gosta de correr e cozinhar.

COMPONENTE

O professor Elon Lages Lima pediu que ficasse registrado o seu protesto pela substituição da expressão “as componentes” da versão original de seu artigo por “os componentes” na versão publicada na RPM 41, já que, embora haja dicionários que afirmem ser “componente” um substantivo masculino, há também aqueles que afirmam ser “componente” um substantivo masculino ou feminino