Flavio Wagner Rodrigues
IME - USP

“Estatisticamente, morri há três anos e quatro meses”
Jaguar na revista Veja de 16/12/98

Neste artigo serão discutidas algumas idéias intuitivas que estão por trás da Teoria Estatística da Estimação, que é a base teórica para a análise de pesquisas eleitorais. Serão apresentadas as principais fontes dos erros que podem ocorrer, discutindo-se também a possibilidade de que eles efetivamente ocorram.

A principal razão que nos levou a escrever este artigo foram os fatos ocorridos na eleição de 1998, quando alguns erros de previsão dos institutos de pesquisa levantaram suspeitas quanto à lisura de seus procedimentos, chegando-se até a falar na apresentação de um projeto proibindo a divulgação dos resultados de pesquisas eleitorais.

Gostaríamos de deixar claro que nunca trabalhamos para nenhum instituto de pesquisa e nem temos nenhuma procuração para defendê-los. Temos, no entanto, duas fortes razões para acreditar que os poucos erros cometidos não foram intencionais. A primeira delas é a reputação dos institutos envolvidos, que têm uma longa história de seriedade e competência na realização de pesquisas. A segunda, mais pragmática, é que, embora as pesquisas eleitorais estejam longe de ser a principal fonte de renda desses institutos, elas são um importante fator de prestígio, que contribui para que eles consigam projetos mais rendosos.

Mais do que ninguém, portanto, os institutos querem acertar e as razões pelas quais eles nem sempre conseguem é o que tentaremos mostrar a seguir.

Serão consideradas apenas as pesquisas de intenção de voto, isto é, aquelas que são feitas antes da realização das eleições. As pesquisas de boca de urna (nas quais o eleitor que acabou de votar é entrevistado) e as pesquisas que se baseiam em contagens parciais já efetuadas não serão consideradas aqui.

Numa pesquisa de intenção de voto o conjunto de interesse (que os estatísticos chamam de universo) é formado por todos os eleitores aptos a votar naquela eleição. É claro que problemas de tempo e de custo tornam impraticável a consulta a todos os elementos desse conjunto. Temos que nos contentar em ouvir apenas uma pequena parcela dessa população e é esse conjunto de eleitores escolhidos para serem entrevistados que recebe o nome de amostra.

Para os estatísticos, uma boa amostra deve poder ser pensada como um retrato, em tamanho pequeno, do universo que está sendo considerado. Assim, por exemplo, nenhuma pessoa de bom-senso entrevistaria apenas moradores das mansões do Morumbi, em São Paulo, ou somente habitantes das favelas da periferia da cidade.

Os principais fatores utilizados para definir a composição da amostra são o nível sócio-econômico, grau de instrução, idade, etc. A escolha desses fatores é em grande parte determinada pela experiência passada, podendo em alguns casos refletir uma opinião pessoal do pesquisador que acredita que um determinado fator é importante para o problema considerado.

Resumindo, durante a realização de uma pesquisa existe uma proporção desconhecida de eleitores que pretendem votar num determinado candidato. Após a conclusão das entrevistas, obtemos a proporção de eleitores da amostra que manifestaram sua preferência por esse candidato. O problema agora é como usar essa informação para obtermos uma estimativa para a proporção de eleitores desse candidato na população. Veremos, nas próximas seções, como isso pode ser feito.

Provavelmente o conceito estatístico mais utilizado no dia-a-dia é a média. Expressões tais como renda média e vida média aparecem com freqüência nas nossas conversas diárias, nos jornais e revistas e a televisão está sempre garantindo que 9 em cada 10 donas de casa preferem o sabão X.

O uso bastante difundido é talvez responsável pelas interpretações erradas que são dadas ao conceito de média. O desejo de ganhar discussões com argumentos que julgamos definitivos nos leva a atribuir à média poderes e propriedades que ela não tem. A idéia pouco precisa que as pessoas têm sobre a média dá origem aos comentários irônicos e divertidos que são feitos sobre ela. Entre os mais conhecidos está aquele do homem com um metro e oitenta de altura que morreu afogado num rio cuja profundidade média era de um metro e cinqüenta. O comentário jocoso do cartunista Jaguar que aparece no início deste artigo poderia até ser complementado (com uma dose de humor negro) com um agradecimento a todos aqueles que morreram antes de atingir a idade média do brasileiro e dessa forma contribuíram (sem alterar a média) para que ele vivesse mais um pouco.

Vamos recordar, através de um exemplo, a definição de média ou esperança matemática de uma distribuição de probabilidades. O lançamento de um dado perfeito admite como resultado qualquer um dos números  1, 2, 3, 4, 5  ou  6,  a cada um deles sendo atribuída probabilidade . A média dessa distribuição é definida como sendo a soma dos produtos de cada resultado possível pela probabilidade correspondente.

Vale a pena observar que essa definição é análoga à definição de centro de gravidade de uma distribuição de massas. Assim como ocorre com o centro de gravidade, a média é o valor central da distribuição, o ponto de equilíbrio, com as massas substituídas pelas probabilidades.

Vamos considerar agora uma situação real na qual um dado perfeito é lançado 1000 vezes e calcula-se a média aritmética dos resultados obtidos. Essa média dificilmente será igual a 3,5, mas resultados bastante gerais nos permitem afirmar que a probabilidade de que ela se afaste muito de 3,5 é bastante pequena. Portanto, se a média teórica fosse desconhecida, esse experimento nos daria uma idéia sobre o seu valor. É importante observar que, ao contrário da média teórica, a média aritmética de 1000 observações não é constante, isto é, se alguém repetir esse experimento nas mesmas condições, irá, quase certamente, encontrar um valor diferente daquele que obtivemos.

É claro que o conhecimento apenas da média de uma distribuição não nos dá muita informação sobre ela. Assim, por exemplo, se em três faces de um dado perfeito for colocado o número 1 e nas outras três o número 6 (e portanto o 1 e o 6 irão aparecer com probabilidade  cada um), a média dessa distribuição será também igual a 3,5, embora ela seja bastante diferente da distribuição associada a um dado comum. Como não poderia deixar de ser, a média nos dá apenas o centro da distribuição, não fornecendo nenhuma informação sobre como os demais valores se situam com relação ao centro. Para medir esse efeito, que os estatísticos chamam de variabilidade, a medida mais utilizada é a variância.

A variância de uma distribuição nunca é negativa e a determinação positiva da raiz quadrada da variância recebe o nome de desvio padrão. É interessante observar que, embora existam infinitas distribuições com a mesma média e mesma variância, o conhecimento da média e da variância permite que se façam afirmações bastante gerais sobre os valores da distribuição. De fato, pode-se mostrar que o intervalo com centro na média e semi-amplitude igual a 2 desvios padrões contém, no mínimo, 75% dos valores da distribuição.

Quando dispomos de informações adicionais, essas estimativas podem ser bastante melhoradas. Assim, por exemplo, para variáveis contínuas com distribuição normal, esse mesmo intervalo conterá, no mínimo, 95% dos valores da distribuição. Esses resultados são bastante utilizados na clínica médica. São eles que possibilitam a construção das tabelas e dos gráficos que os pediatras utilizam para acompanhar o desenvolvimento das crianças com relação ao peso e à altura. Os intervalos de normalidade para os resultados de exames laboratoriais são também determinados com base nessa teoria. Fica fácil agora explicar as brincadeiras que são feitas sobre a média. Dependendo do valor da variância é bastante provável que um rio cuja profundidade média é igual a um metro e meio tenha pontos onde a profundidade supere um metro e oitenta. Da mesma forma a variância da distribuição do tempo de vida do brasileiro mostra que não só é possível, como até bastante provável que alguém viva três ou quatro anos a mais. A única coisa a se lamentar é que também seja possível e até provável que muitos morram antes de atingir a idade média.

Nos meses que antecedem uma eleição encontramos com freqüência nos jornais informações que dizem que, de acordo com o instituto X, o candidato A tem 37% das intenções de voto e que a margem de erro da pesquisa é de dois pontos percentuais para mais ou para menos. Essa informação significa que, na amostra colhida pelo instituto, 37% dos entrevistados manifestaram sua preferência pelo candidato A e que, com uma probabilidade conhecida, que quase nunca é mencionada mas que geralmente vale 95%, o valor real da proporção de eleitores de A está compreendida entre 35 e 39%.

Para ver como esse intervalo é determinado, seja  p  a proporção de eleitores que pretendem votar num candidato A.  Vamos admitir que  p  é estritamente positiva e diferente de 1. Suponhamos que, numa amostra de n  eleitores,  k  manifestem a intenção de votar em  A.  A proporção dos eleitores da amostra que pretendem votar em  A  será denotada por valor diferente para p*. Utilizando a distribuição binomial de probabilidades podemos teórico importante nos permite mostrar que, para valores grandes de  n,  p*  tem uma distribuição aproximadamente normal.

Uma consulta à tabela da normal mostra que, se z tem uma distribuição normal com média zero e variância 1, temos: P(-1,96 < z < 1,96) = 95%.   Segue-se que a probabilidade de igual a  95%.  O problema que ainda resta é que os extremos desse intervalo dependem do valor desconhecido de  p.  Uma solução possível é aumentar o intervalo substituindo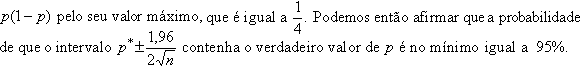

Assim, por exemplo, se desejarmos uma confiança de 95% e uma margem de erro de dois pontos percentuais (para mais ou para menos),  n deverá satisfazer:

Na determinação de um intervalo de confiança lidamos com três quantidades inter-relacionadas, que são as seguintes:

1.    O tamanho da amostra  n.

2.    A precisão da estimativa que é definida pela amplitude do intervalo.

3.  A confiança depositada no intervalo que é definida pela probabilidade de que o intervalo contenha o verdadeiro valor de  p.

Assim, por  exemplo, se o tamanho da amostra permanece fixo, um aumento da precisão implica necessariamente uma diminuição da confiança e reciprocamente. A única maneira de melhorar a precisão sem alterar a confiança é aumentar o tamanho da amostra. Analogamente, se estivermos dispostos a aceitar uma redução da confiança, a mesma precisão poderá ser obtida com uma amostra de tamanho menor. Se no exemplo anterior trabalharmos com uma confiança de 90% (o que corresponde a substituir o valor  1,96   por  1,64),  o tamanho da amostra se reduzirá de 2401  para  1681.

Finalmente, é importante observar que a confiança e a precisão estão relacionadas com  n  e, assim, para manter a confiança e reduzir o intervalo à metade, nós vamos precisar de uma amostra quatro vezes maior. O preço a ser pago em termos de custos e do tempo necessário para obter as informações nem sempre compensa os ganhos de precisão.

Nesta seção nós vamos discutir uma possível fonte de erro que muitas vezes não é sequer considerada pelos pesquisadores. Suponha que o número de elementos da amostra foi determinado, bem como os critérios que irão reger a sua composição. Resta definir o processo que será utilizado para selecionar os elementos que serão entrevistados. O saudoso professor José Severo de Camargo Pereira, que, entre os estatísticos que conheci, era o que mais sensibilidade tinha para os problemas dessa área, costumava contar uma história bastante ilustrativa sobre o que pode acontecer de errado no processo.

Um estudo foi realizado para determinar os gastos com alimentação de famílias de baixa renda na periferia da cidade de São Paulo. Pequenas vendas e mercados eram visitados, perguntando-se a pessoas escolhidas ao acaso o custo da compra que estavam fazendo no momento. Os valores encontrados na pesquisa foram significativamente maiores do que aqueles que eram esperados. Convidado para participar da análise dos resultados, o professor Severo descobriu que os pesquisadores entrevistavam a pessoa que se encontrava no caixa no momento em que eles chegavam à loja. A explicação para os valores mais altos estava no fato de que quem gastava mais ficava mais tempo no caixa e tinha portanto uma probabilidade maior de ser incluído na amostra.

Nas pesquisas eleitorais, esse problema surge devido ao processo de seleção adotado pela maioria dos institutos, que consiste em entrevistar pessoas escolhidas entre as que passam pelos pontos mais movimentados das grandes cidades. É claro que, embora muita gente passe por esses pontos, existe um número maior de pessoas que raramente ou nunca passa por lá. Se por alguma razão esses dois grupos tiverem opiniões diferentes sobre a eleição, os resultados finais serão distorcidos. Infelizmente, no entanto, esse é um erro provável que é praticamente impossível de ser evitado. A adoção de um plano de amostragem por domicílios, que envolva a visita dos pesquisadores à casa do eleitor, teria um custo proibitivo e seria muito demorado em razão da rapidez que geralmente é exigida pelos patrocinadores das pesquisas eleitorais.

Neste artigo procuramos dar uma idéia dos problemas que podem surgir durante a realização de uma pesquisa de intenção de voto, levando eventualmente a erros de previsão como os poucos que ocorreram nas eleições de 1998. Além desses problemas de ordem técnica, existe ainda a possibilidade de que o aparecimento de fatos novos contribua para uma mudança radical na intenção dos eleitores. Apenas para citar um exemplo recente no segundo turno das eleições de 1998 em São Paulo, a virada que ocorreu só foi detectada pelos institutos de pesquisa na última semana que antecedeu a eleição.

Os defensores da idéia de que as pesquisas sejam proibidas (ou pelo menos que seus resultados não sejam divulgados) argumentam que a divulgação das pesquisas teria uma forte influência no resultado final da eleição. Essa idéia que pesquisa ganha eleição faz lembrar uma frase atribuída ao técnico João Saldanha, que costumava dizer que, se macumba ganhasse jogo, o campeonato baiano terminaria empatado.

A justificativa para essa crença seria a existência de muitos eleitores que olhariam para a eleição como se ela fosse uma corrida de cavalos e procurariam votar (ou seria melhor dizermos apostar) no vencedor. É claro que existem eleitores com esse tipo de comportamento, mas eu nunca vi um estudo sério que mostre que o número deles seja significativo. Vale a pena observar que, se existissem muitos eleitores desse tipo, os candidatos que saíssem na frente nas primeiras pesquisas seriam beneficiados pelo apoio desses eleitores e terminariam ganhando a eleição, o que nem sempre ocorre.

Não há dúvida que as pesquisas devem ser mais controladas pela imprensa, pelo Congresso e pela sociedade como um todo. É necessário que todas as informações sobre cada pesquisa estejam disponíveis, permitindo assim que a sua seriedade seja avaliada. A idéia de proibir a realização de pesquisas ou impedir a divulgação dos seus resultados não me parece aceitável. De uma ou de outra maneira as pesquisas continuariam a ser realizadas e uns poucos privilegiados continuariam tendo acesso aos seus resultados. Os jornalistas seriam estimulados a criar meios para divulgar esses resultados na seção de esportes ou de caça e pesca sob uma forma camuflada. O eleitor menos privilegiado que não freqüenta os meios intelectuais ou acadêmicos e só recebe notícias pela televisão acabaria sendo o grande prejudicado. Na reforma política que deve brevemente ser discutida no Congresso, existem problemas muito mais importantes para serem tratados do que essa proibição, que negaria ao eleitor menos favorecido o acesso a informações que estariam disponíveis.