Jaime Poniachik
Argentina

Em uma tira com  n  casas, dois jogadores alternam-se, colocando nas casas uma ficha de cada vez. Um coloca fichas brancas, o outro, pretas, sempre em casas que estiverem vazias. A partida acaba quando não existirem mais casas vazias. Contam-se, então, os “impactos”. Há impacto quando duas casas vizinhas tiverem fichas de cores distintas. Se, no final, a quantidade de impactos for ímpar, Branco ganha a partida; se for par, ganha o Preto. O diagrama mostra uma partida terminada. Os impactos estão marcados com estrelas. Houve 5 impactos. Branco ganhou.

Branco começa. Qual é a estratégia vencedora?

Resposta
O jogo dos impactos não é mais do que a apresentação lúdica de um resultado matemático bastante conhecido, o “Lema de Sperner”, aplicado, em nosso caso, a um segmento. Diz o lema:

Em um segmento, dividido em segmentos menores, marcamos o extremo esquerdo com 0, o direito com 1 e cada ponto de divisão intermediário com 0 ou 1. Dizemos que um segmento é “bom” se os seus extremos estiverem marcados com números distintos.

a)   Demonstra-se que o número de segmentos bons é ímpar.

b)  Demonstra-se que os segmentos bons do tipo  (0, 1)  são um a mais do que os segmentos bons do tipo  (1, 0).

A demonstração é muito simples e engenhosa:

Contam-se os segmentos bons indo da esquerda para a direita. O 1 que estiver mais à esquerda fecha o primeiro segmento bom que é de tipo    (0, 1). O próximo segmento bom deverá ser de tipo (1, 0).

E, sucessivamente, os segmentos bons irão alternando-se entre os de um e de outro tipo. O último será do tipo (0 1).

Daí concluí-se que a quantidade de segmentos bons é ímpar e que há um segmento a mais do tipo (0,1) que o do tipo (1, 0).

Observações: Se os extremos do segmento inicial receberem ambos o mesmo rótulo, a quantidade de segmentos bons será par e haverá tantos segmentos de um tipo quanto do outro.

Voltemos ao jogo dos impactos. Para ganhar, Branco apenas precisa assegurar que os extremos tenham fichas de cores distintas. Isso é fácil: ele joga fichas, à vontade, nas casas internas e, assim que Preto colocar uma ficha em uma das extremidades, Branco coloca sua ficha na outra extremidade.

As mesmas regras poderiam ser usadas em tabuleiros mais complexos. Por exemplo:

Qual é a estratégia para ganhar?

Uma linha contínua que começa subindo e termina descendo tem um número ímpar de extremos (máximos e mínimos).

Numa tira de  n  casas escrevem-se os números 1, 2, 3, ..., n  da seguinte maneira: cada jogador escreve um número por vez numa casa livre, número que até então não tenha sido usado. A partida termina quando todas as casas estiverem preenchidas. Se resultar uma quantidade ímpar de extremos, a vitória será do primeiro jogador; se a quantidade for par, ganhará o segundo. O diagrama mostra uma partida acabada:

Jogando um tabuleiro quadriculado, a partida anterior ficaria assim:

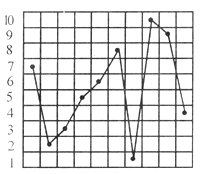
Qual a estratégia para ganhar?

O Lema de Spener completo refere-se à triangulação de triângulos, equivalente ao que foi nossa segmentação de segmentos. Ele diz:

Um triângulo, cujos vértices estão marcados com os números 1, 2 e 3, é dividido em triângulos e os novos vértices são numerados com esses três algarismos, respeitando a seguinte condição de fronteira: todo novo vértice que cair em um lado do triângulo maior levará um dos algarismos dos extremos desse lado. Demonstra-se que pelo menos um dos triângulos da partição está numerado com três algarismos distintos. E mais, o número total desses triângulos é ímpar.

Emannuel Sperner  (1905-180) foi um matemático alemão, que em 1928 demosntrou o lema da partição do triângulo (e, em geral, do simplexo n-dimensional). Um lema é, em Matemática, uma proposição simples que antecede um teorema. O de Sperner antecede o teorema do ponto fixo.
Para maiores detalhes e extensões veja, Yu Shashkin. Pontos fixos. Editora Mei, Moscou, 1991.