|
Sérgio
Alves
IME - USP
Envie suas perguntas para:
RPM - O leitor pergunta
Caixa Postal 66281
05315-970 São Paulo, SP
|
 |
Um leitor de Marília, SP, nos pede a
solução do seguinte problema: Uma empresa vende habitualmente café em pacotes
de 1 quilo. Numa tentativa de aumentar suas vendas, passa a
comercializar o café em embalagens contendo 20% a mais de café, mantendo
o mesmo preço dos pacotes de 1 quilo. Em que porcentagem foi reduzido o preço
do quilo de café?
RPM:
Durante a promoção, 1,2 quilo
de café passou a custar p, sendo p o preço de 1 quilo
anterior à promoção. Assim


 Dois
leitores, um de Curitiba, PR, e outro de Porto Alegre, RS, nos enviaram o
problema: Quatro retas se cortam formando quatro triângulos como na figura.
Mostrar que as circunferências circunscritas aos quatro triângulos têm um ponto
em comum. Dois
leitores, um de Curitiba, PR, e outro de Porto Alegre, RS, nos enviaram o
problema: Quatro retas se cortam formando quatro triângulos como na figura.
Mostrar que as circunferências circunscritas aos quatro triângulos têm um ponto
em comum.

RPM:
Esse resultado é conhecido como Teorema de Miquel, que o descobriu em 1938,
e o ponto comum obtido é chamado ponto de Miquel. Iniciamos a demonstração com
um resultado preliminar:
Dado um triângulo
 e, sendo e, sendo
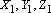 pontos arbitrários sobre os lados YZ, XZ,
XY respectivamente, então as três circunferências pontos arbitrários sobre os lados YZ, XZ,
XY respectivamente, então as três circunferências
 e e  têm um ponto em comum. têm um ponto em comum.
|
A prova desse resultado é simples. Na
figura ao lado, temos que as circunferências
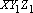 e e 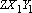 se cortam em se cortam em
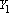 e também num ponto que chamaremos M. e também num ponto que chamaremos M. |
|
|
|
|
|
|
|
|
 Deixamos
para o leitor a verificação de que o resultado que acabamos de provar continua
válido se os pontos Deixamos
para o leitor a verificação de que o resultado que acabamos de provar continua
válido se os pontos 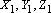 estiverem nas retas dadas por YZ, XZ, XY,
não necessariamente nos lados do triângulo. estiverem nas retas dadas por YZ, XZ, XY,
não necessariamente nos lados do triângulo.
Por outro lado, aplicando o resultado para o
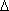 AB1C1 e
para os pontos A1, B, C temos que as três
circunferências ABC, B1A1C e C1A1B
têm um ponto em comum. Como os únicos pontos comuns dessas últimas duas
circunferências são A1 e M, concluímos que as quatro circunferências AB1C1 e
para os pontos A1, B, C temos que as três
circunferências ABC, B1A1C e C1A1B
têm um ponto em comum. Como os únicos pontos comuns dessas últimas duas
circunferências são A1 e M, concluímos que as quatro circunferências
AB1C1, BA1C1,
CA1B1 e
ABC
têm um ponto em comum, o que conclui a prova.

|
Respostas dos Probleminhas |
|
1. Paulo e Vera, Luiz e
Célia, José e Maria. 2. 10 3.
Daniel. |
|