|
Paulino
Liu
São
Paulo, SP
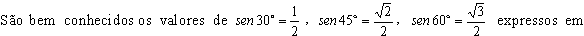radicais. O curioso
é que, a partir desses e outros valores, é possível construir uma
tabela dos valores das funções trigonométricas dos ângulos múltiplos
de três, 3o, 6o,
9o, 12o, 15o, ... , 87o, 90o,
escritos também com expressões que só envolvem radicais quadráticos,
isto é, números racionais, suas raízes quadradas, ou combinações
dessas com as “quatro operações”.
|
Cálculo
de alguns valores
|
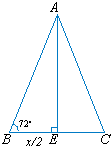
Vamos
determinar geometricamente uma expressão para
cos 72°
.
|
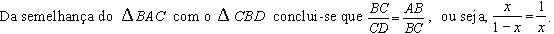
Resolvendo
essa equação do 2o grau,
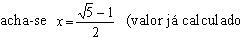na RPM
29, pág. 44).
Sendo
E
médio de BC,
vem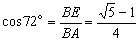 
.
|
|
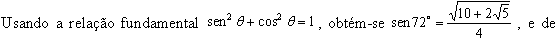
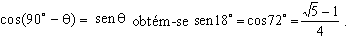
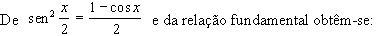
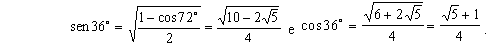
Daí
podemos obter, por exemplo,
.
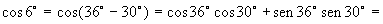
Ou
ainda, usando as fórmulas
,
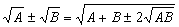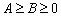, podemos escrever
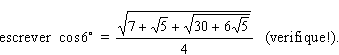
Utilizando
novamente a fórmula do “arco-metade”, obtêm-se:
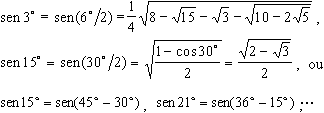
Observe
que, se for possível obter
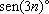como uma expressão que só
envolva radicais quadráticos, então será possível, através da relação
fundamental, obter
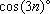e, em seguida,
+
,
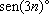
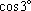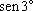
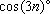também
como uma expressão dessa forma. Portanto, como já temos
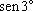, obteremos (de novo!)
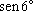, depois
,
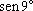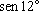e, por indução,
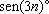para todo
n.
Alguns
valores obtidos:
Cabe
a pergunta:
Qualquer
seno ou cosseno pode ser escrito dessa maneira?
A
resposta é não! Aliás, a
propriedade em questão só é uma curiosidade por causa desse não.
Por exemplo,
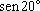não pode ser escrito como uma expressão que só envolva radicais quadráticos.
Para uma demonstração disso, veja, por exemplo: Construções
possíveis com régua e compasso, de J.P.G. Carneiro, no apêndice do
livro Construções geométricas
-
Coleção do Professor de Matemática, de autoria de Eduardo Wagner,
IMPA/VITAE, 1993. Nessa referência também poderá ser verificado que os
números que podem ser escritos como uma expressão que só envolva
radicais quadráticos são justamente os que podem ser construídos com régua
e compasso. E, mais, quando
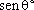(ou cosseno) for uma expressão 
|
