Geraldo Ávila
UFG -GO

     A circunferência

Os autores de livros didáticos, ao tratarem da circunferência, da elipse e da hipérbole, cometem excessos e omissões. Assim, no caso da circunferência, eles se preocupam em pesquisar a equação geral do 2o grau, em  x  e  y,

para determinar as condições que os coeficientes devem satisfazer para que a equação represente uma circunferência. Ora, isso é desnecessário; basta observar que a condição necessária e suficiente para que um ponto    pertença à circunferência de centro    e raio  r  é que   satisfaça a equação

,

ou seja,

.

Daqui decorre que a equação de qualquer circunferência é do tipo

as coordenadas do centro sendo dadas por    e  ,  e o raio por  propósito, a RPM 29 traz um interessante artigo do Professor Elon Lages Lima, no qual ele aponta erros em que incorrem os livros ao discutirem essa equação (1).

 

     A elipse  

Os mesmos autores, ao tratarem a elipse, provam que se o ponto   pertence à elipse de semi-eixos  a  e  b,  disposta simetricamente em relação aos dois eixos de coordenadas, então    satisfaz a equação

Mas isso não basta para provar que essa é a equação da elipse; é preciso demonstrar também a recíproca: se    satisfaz a equação  (2), então esse ponto pertence à elipse de semi-eixos  a  e  b,  disposta simetricamente em relação aos eixos de coordenadas. Essa omissão não acontece só nos livros do ensino médio, mas também nos livros universitários de Geometria Analítica. Faremos adiante a demonstração desse fato.

 

      Apenas uma recordação  

Primeiramente vamos recordar alguns pontos para compreensão do que vem a seguir. A elipse costuma ser definida como sendo o lugar geométrico dos pontos  P  do plano, cuja soma das distâncias a dois pontos fixos  F  e F'   é constante.

Isso significa que, se  P, P' , P''   etc. são pontos da elipse, então (Figura 1):

 

  Figura 2

Uma elipse pode ser desenhada com o auxílio de uma linha com as pontas amarradas em dois preguinhos ou alfinetes fixados em  F   e  F'   e por um lápis, como indica a Figura 2. Mantendo-se a linha esticada e movendo-se o lápis no papel, obtemos uma elipse, já que a soma das distâncias  PF   e  PF'   mantém-se constante.

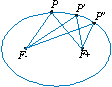
Os pontos  F e F' são os focos da elipse e o ponto médio do segmento  FF' é o seu centro.

Vamos supor a elipse centrada na origem e disposta simetricamente em relação a cada um dos eixos de coordenadas, de forma que o eixo  Ox   seja coincidente com  OF'   (Figura 3).

Sejam  -c   e    as abscissas de  F   e  F'   , respectivamente, e seja  2a   a constante  ,  onde    é um ponto arbitrário da elipse.


Figura 3

Pondo    e  ,  e notando que

a equação da elipse,   (3), assume a forma

.

(4)

Para eliminarmos os radicais, elevamos ambos os membros dessa equação ao quadrado, donde resulta

(5)

ou ainda, após simplificações,

.

(6)

O radical desaparece com uma nova operação de elevar ao quadrado:

,

   (7)

isto é,

,

 

que equivale a

.

(8)

Observe que  ;  logo, pondo  e dividindo ambos os membros de  (8)  por  ,  obtemos finalmente a equação 

.

(9)

Voltamos a insistir em que ainda não podemos dizer que esta é a equação da elipse, pois provamos apenas que ela é condição necessária para que um ponto    pertença à elipse. Falta provar que a condição é suficiente, como faremos logo adiante.  

 

     Para demonstrar a recíproca  

O que acabamos de fazer foi provar que  (3)  Þ  (9). Devemos estabelecer a recíproca 
- (9)  Þ  (3) -  para nos certificarmos de que essas duas equações são equivalentes. Essa preocupação é legítima porque usamos duas vezes a operação de elevar ao quadrado, uma operação que freqüentemente introduz novas soluções na equação em que atua. Por exemplo, ,  mas  ,  de sorte que ao elevar ao quadrado introduzimos a raiz  . Não podemos, pois, escrever  . Em outras palavras, é sempre verdade que  , mas nem sempre  . Todavia, isso é sempre verdade, desde que saibamos, de antemão, que  a  e  b  são números positivos. Nesse caso, sim, podemos escrever  . Vamos colocar isso em destaque:

(10)

 

     Demonstrando a recíproca  

Feitas essas observações, fica fácil demonstrar de vez que   (9) (3), o que engloba a recíproca     (9)  Þ  (3).

Começamos observando que as equações  (3)  e  (4)  são idênticas, (4) sendo apenas outra maneira de escrever a  (3). As equações  (4)  e  (5) são equivalentes porque já sabemos, de antemão, que  d  e    são números positivos, quaisquer que sejam os valores de  x  e  y;  d  e    desempenham aqui os mesmos papéis que  a  e  b desempenham em (10). As equações  (5)  e  (6)  são equivalentes porque  (6) resulta de  (5)  por simplificações todas reversíveis. Vejamos agora a passagem de  (6)  a (7): os parênteses no radical de  (6)  são    e  , positivos; e é também positivo o membro direito de  (6),  de forma que  (6)  e  (7) são equivalentes pela mesma razão que prova a equivalência de  (4)  e  (5). Finalmente,  (9)  resulta de  (7)  por transformações todas elas reversíveis. Isso completa a demonstração de que  (3)  e  (9)  são equivalentes.

 

     A hipérbole  

O caso da hipérbole é análogo ao da elipse. Vejamos: a hipérbole é definida como sendo o lugar geométrico dos pontos P do plano, cuja diferença das distâncias a dois pontos fixos  F   e  F'   é uma constante  2a . Mas a hipérbole possui dois ramos (Figura 4), conforme seja

Figura 

 

 

.

 

(11)

Essa equação é a análoga da (4). A partir dela, procedendo como no caso da elipse, somos levados, sucessivamente, às seguintes equações:

 

   (12)

,

 (13)

,

(14)

.

(15)

Observe que, enquanto no caso da elipse,  ,  agora, no caso da hipérbole,  .  Pondo, então,  ,  a última equação nos dá, após divisão por  :

.

(16)

As equivalências  (12)    (13),  (13)    (14)  e  (14)    (15)  são justificadas como no caso da elipse. Falta provar que  (12)  Þ  (11),  visto que já provamos  (11)  Þ  (12)  ao deduzirmos esta última equação. Mas a prova de que  (12)  Þ  (11)  segue por extração da raiz quadrada de  (12). De fato, ao fazermos isso, obtemos as duas possibilidades indicadas em  (11)  pelo duplo sinal do 1o membro. Observe que ambas essas possibilidades conduzem a valores positivos do 1o membro, cada um correspondendo a um ramo da hipérbole; num caso temos  ;  no outro,  .