|
|
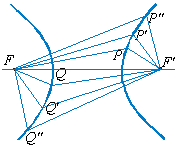
Assim, com referência à Fig.
2,
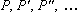 são pontos da hipérbole, visto que
são pontos da hipérbole, visto que
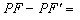
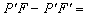
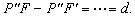
Do mesmo modo, Q,, Q',
Q",... , satisfazendo as condições
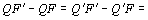
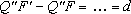 , também pertencem à hipérbole, a qual, portanto, possui dois ramos
distintos.
, também pertencem à hipérbole, a qual, portanto, possui dois ramos
distintos. |
|
F e
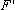 são chamados focos da hipérbole.
são chamados focos da hipérbole.
Vamos imaginar um espelho refletor
construído com o formato de um ramo de hipérbole, a parte refletora
estando do “lado de fora” da hipérbole, isto é, na sua parte côncava.
|
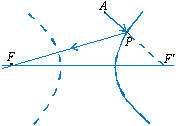
Fig. 3
|
Suponhamos que um raio de luz
proveniente de um ponto A incida no espelho em P, como
ilustra a Fig. 3, de forma que a reta AP passe pelo foco
F' . Então o raio refletido terá de passar pelo outro foco F
. Esta propriedade será demonstrada mais adiante. |
Deixando-a de lado por um momento,
vamos explicar uma de suas aplicações na construção de telescópios.
Galileu Galilei (1564-1642) foi o primeiro
cientista a construir um telescópio para observação astronômica. Isso se
deu em 1609 e resultou em notáveis descobertas: Galileu viu montanhas e
acidentes geográficos na superfície lunar, observou que Vênus passa por
fases como a Lua, notou que Saturno tem um formato alongado (devido a
seus anéis), e que Júpiter possui satélites girando a sua volta. Em
pouco tempo Galileu revolucionou a Astronomia.
Os primeiros telescópios, inclusive o de
Galileu, foram construídos com lentes e funcionavam com base na refração
da luz. São os chamados telescópios refratores.
Acontece que as lentes têm vários
inconvenientes, como as deformações das imagens que elas produzem,
fenômeno que pode ser facilmente observado com qualquer lente de grau de
óculos comuns; basta olhar através da lente e movê-la transversalmente
para um lado e para o outro, ou em círculos, para notar essas
deformações.
Além disso, a lente também atua como um
prisma, decompondo a luz branca em várias cores, produzindo outro tipo
de efeito indesejável nas observações, as chamadas aberrações
cromáticas.
Esses inconvenientes dos telescópios
refratores não existem nos telescópios refletores. O telescópio
refletor nada mais é do que um espelho parabólico no fundo de um tubo,
como ilustra a Fig. 4. Os raios provenientes de um corpo celeste
distante (estrela, galáxia, planeta, etc.) formam um feixe praticamente
paralelo, que se reflete no espelho e vai formar a imagem do objeto no
foco F.
|
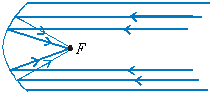
Fig. 4
|
O problema agora é que, para
observar essa imagem, o observador teria de estar com seu olho
posicionado no foco da parábola, mas isso é impossível na prática.
|
Isaac Newton (1642-1727)
resolveu esse problema em seu telescópio refletor, colocando um espelho
plano E entre o espelho parabólico e o foco F (Fig. 5).
Com isso, os raios que iriam formar a imagem em F são novamente
refletidos e vão formar essa imagem num ponto
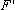 fora do tubo do telescópio, onde se posiciona o observador.
fora do tubo do telescópio, onde se posiciona o observador.

Fig. 5
|
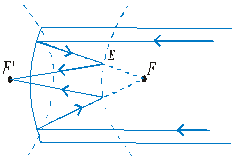 Fig. 6
Fig. 6
|
Em 1672 o astrônomo francês
Cassegrain propôs a utilização de um espelho hiperbólico E,
como ilustra a Fig. 6, em lugar do espelho plano de Newton. Um dos
focos da hipérbole coincide com o foco F da parábola.
|
Agora os raios que iriam formar a
imagem no foco F são refletidos pelo espelho E e
formarão essa imagem no outro foco F' da hipérbole.
Para compreender a vantagem desse
espelho hiperbólico de Cassegrain sobre o espelho plano de Newton,
devemos observar que o espelho plano não pode ficar muito próximo do
foco F, sob pena de o ponto F' da Fig. 5 ficar
dentro do telescópio; em conseqüência, o espelho plano precisa ser de
razoável tamanho, o que resulta num bloqueio significativo da luz
incidente no espelho parabólico que forma a parte principal do
telescópio.
O espelho de Cassegrain, pelo
contrário, pode ser construído mais próximo ou mais afastado do foco
F, mantendo-se fixa a distância FF' entre os focos da
hipérbole; em conseqüência, o tamanho desse espelho pode ser maior ou
menor. A distância entre os focos F e F' também pode
ser alterada para mais ou para menos, sem mudar a posição do foco F.
A combinação desses fatores permite grande flexibilidade na montagem do
refletor hiperbólico E, adequando-a, assim, às
exigências das observações.
Essas montagens de Cassegrain
somente começaram a ser utilizadas nos telescópios cerca de um século
após terem sido propostas. Desde então passaram a ser largamente usadas,
e hoje em dia estão presentes, não apenas nos telescópios óticos, mas
também nos radiotelescópios.
O famoso telescópio ótico do
observatório de Monte Palomar, que fica 80 km a nordeste de San Diego,
na Califórnia, utiliza várias montagens do tipo de Cassegrain.
|
Prova de que o
raio refletido passa por F |
Finalmente, vamos demonstrar que
um raio incidente que passa por um dos focos do espelho hiperbólico
produz um raio refletido que passa pelo outro foco.
A demonstração será feita da
seguinte maneira: provaremos que a bissetriz do ângulo FPF'
(Fig. 7) é ao mesmo tempo a reta tangente à hipérbole em P.
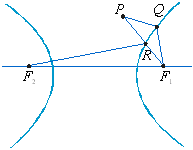
Fig. 7
Na Fig.7, R é ponto de intersecção
da reta PF, com a hipérbole. Provaremos, inicialmente, que PRF2
é o caminho mais curto que vai de P a F2,
tocando um ponto da hipérbole. Com efeito, sendo Q um outro ponto
da hipérbole, diferente de R, teremos
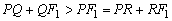 ; ;
e como Q e R estão na
hipérbole,
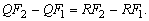
Somando esta igualdade à desigualdade
anterior, obtemos
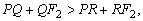 ou seja,
ou seja, 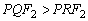
que é o resultado desejado.
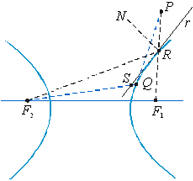
Fig. 8
Vamos provar agora que o caminho mínimo é
aquele seguido pela luz. Para isso, com referência à Fig. 8, seja PRF2
o caminho seguido pela luz, isto é, tal que o ângulo de incidência
PRN seja igual ao ângulo de reflexão NRF2, sendo
RN a normal à hipérbole em R. Tracemos a reta r
tangente à hipérbole em R. Seja PQF2 um outro
caminho, cortando a reta tangente em S. Como
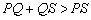 e e
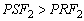 ,
concluímos que ,
concluímos que 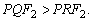 Fica
assim provado que o raio de luz segue o caminho mínimo, isto é, o
caminho PRF2 tal que a reta PR passa pelo foco
F1. Fica
assim provado que o raio de luz segue o caminho mínimo, isto é, o
caminho PRF2 tal que a reta PR passa pelo foco
F1.
|