|
Vera
Helena G. Souza e
Sérgio Alves
IME
-
USP
Envie suas perguntas para:
RPM - O leitor pergunta
Caixa Postal 66281
05315-970
São Paulo, SP
|

|
¨
Um leitor de Marília, SP, nos enviou o seguinte problema: No pentágono desenhado abaixo
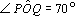 . Sendo x
e y
as medidas dos ângulos
. Sendo x
e y
as medidas dos ângulos
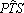 e
e
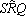 ,
quanto vale
,
quanto vale
 ?
?


RPM:
Tanto
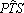 quanto
quanto
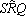 são ângulos inscritos
na circunferência de modo que, pelo teorema do ângulo inscrito, temos
são ângulos inscritos
na circunferência de modo que, pelo teorema do ângulo inscrito, temos
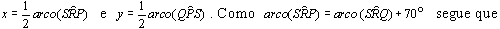
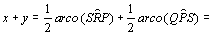
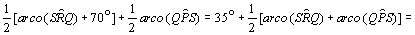
 .
.
¨ Um leitor de Juiz de Fora, MG, apresenta o seguinte
problema: Determine o resto da divisão
do polinômio
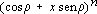 por
por
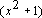 , onde
, onde
 é um número natural e
r
é real fixo.
é um número natural e
r
é real fixo.
RPM:
Fazendo 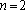 , obtemos
o resto
, obtemos
o resto

1)
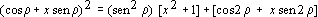 .
.
Se
tomamos
 , obtemos
, obtemos

e
então:
2)
 , onde
, onde
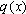 é um polinômio de
grau 1. Em
vista de 1) e 2) é razoável esperarmos que o resto
é um polinômio de
grau 1. Em
vista de 1) e 2) é razoável esperarmos que o resto
 da divisão de
da divisão de
 por
por
 é dado
por
é dado
por
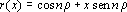 , ou seja,
, ou seja,
3)
 , onde
, onde
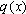 é um polinômio de grau
é um polinômio de grau
(n = 2).
Procederemos
pelo método da indução finita sobre
n.
Já vimos que 3) é verdadeira para
 ( e também para
( e também para
 ). Supondo 3) válida para
). Supondo 3) válida para
 , provaremos que ela continua verdadeira para
, provaremos que ela continua verdadeira para
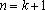 .
.

¨
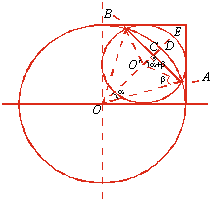
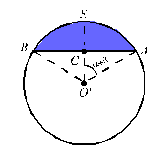
Um leitor de Fortaleza, CE, nos manda o seguinte problema:
|
Calcular a área da parte
hachurada, sabendo que o quadrado tem lado a.
|

|
|
RPM:
Pelos
dados do problema sabemos que os raios das circunferências medem
a e a/2.
A
área procurada será dada por
 , onde
, onde
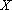 é a área do segmento
circular ABEA
e Y
é a área do segmento circular
ABDA.
é a área do segmento
circular ABEA
e Y
é a área do segmento circular
ABDA.
|
|
|

dos cossenos,
obtemos:
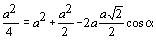 e
e
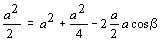 .
.
|
|
|
|
|
|
|


|
|
|

|
|
Temos
X = área do setor
 -
área (
-
área ( ) =
) =

 .
.
|
|
E,
Y = área do
setor
 -
área (
-
área ( ) =
) =

 .
.
|
Concluímos
que a área procurada é igual a

 e
e
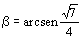 .
.
|
Respostas
dos Probleminhas
|
|
1)
Puccini -
1858, Mahler -
1860, Debussy -
1862, Strauss -
1864.
2)
!
3) 5 832
dias.
|
|