|
Elon
Lages Lima
Dois
dos modelos matemáticos mais utilizados para resolver problemas
elementares são o modelo linear, representado por funções do tipo
y = ax + b, e o modelo exponencial, no qual se empregam as funções do tipo
y = ax + beax. O modelo linear ocorre em praticamente todos os problemas durante os
primeiros oito anos da escola e, com menos exclusividade porém ainda com
grande destaque, nos três anos finais. Por outro lado, o modelo
exponencial só aparece nesses três últimos anos, embora sua importância
seja considerável na universidade, bem como nas aplicações da Matemática
em atividades científicas ou profissionais.
Uma
vez decidido que o modelo adequado para um determinado problema é o
linear ou o exponencial, a partir daí o tratamento matemático da questão
não oferece maiores dificuldades. No primeiro caso, as perguntas são
respondidas com o emprego das quatro operações elementares, às quais se
somam, para o segundo caso, os logaritmos e -
naturalmente -
a própria função exponencial.
As
dúvidas que possam surgir acontecem antes, na escolha do instrumento
matemático apropriado para o problema que se estuda. Os alunos muitas
vezes não sabem qual o modelo a empregar; os professores, freqüentemente,
conhecem a resposta por experiência mas nem sempre são capazes de
justificá-la, mesmo no caso linear.
No
que se segue, apresentaremos critérios de natureza elementar para
reconhecer se uma dada função é do tipo
f(x) = ax + b
ou
f(x) = beax + b. Nos problemas concretos, esses critérios admitem interpretações
intuitivas que podem ser de grande ajuda na escolha do modelo matemático
a ser utilizado.
Nesta
apresentação não é utilizada a noção de limite, e nenhum outro
conceito de natureza infinitesimal.
O
caso mais simples do modelo linear ocorre na situação clássica da
proporcionalidade. Ali, são dadas duas grandezas,
 e
e
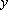 . Diz-se que
. Diz-se que
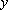 é
proporcional a
é
proporcional a
 quando
os valores de
quando
os valores de
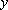 dependem
dos valores de dependem
dos valores de
 , de
tal maneira que ao dobrar, triplicar ou, mais geralmente, tomar , de
tal maneira que ao dobrar, triplicar ou, mais geralmente, tomar
 vezes
a grandeza
vezes
a grandeza
 , o valor correspondente de , o valor correspondente de
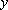 fica
dobrado, triplicado ou, mais geralmente, multiplicado por
fica
dobrado, triplicado ou, mais geralmente, multiplicado por
 . Nesse caso, a função
. Nesse caso, a função
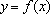 que
modela o problema tem a propriedade
f(nx)
= n . f(x) + b
para
todo valor de
que
modela o problema tem a propriedade
f(nx)
= n . f(x) + b
para
todo valor de
 . Quando as grandezas
. Quando as grandezas
 e
y
podem
assumir valores negativos, a proporcionalidade entre
e
y
podem
assumir valores negativos, a proporcionalidade entre
 e
e
 implica
a igualdade
f(nx) = n . f(x)
para
todo valor de
implica
a igualdade
f(nx) = n . f(x)
para
todo valor de
 e
todo número inteiro
e
todo número inteiro
 .
.
Os
teoremas a seguir estabelecem a Matemática que se aplica a esse tipo de
problema. Os símbolos
N, Z, Q,
IR
e
IR+
indicam respectivamente os conjuntos dos números naturais,
inteiros, racionais, reais e reais positivos.
Lema: Seja
f:IR
 IR
uma função tal que
f(nx)
= n . f(x)
para
todo
x
IR
uma função tal que
f(nx)
= n . f(x)
para
todo
x
 IR
e todo
n IR
e todo
n  Z. Então
f(r
. x) = r . f(x)
para
todo
r Z. Então
f(r
. x) = r . f(x)
para
todo
r  Q
e
todo
x Q
e
todo
x
 IR.
Em
particular, se
a = f(1), tem-se
f(r)=
ar
para
todo
x IR.
Em
particular, se
a = f(1), tem-se
f(r)=
ar
para
todo
x
 Q
.
Q
.
Demonstração: Dado
x
 Q
, tem-se
Q
, tem-se
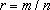 , com
, com
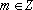 e
e
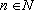 . Então
. Então
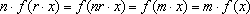 ,
,
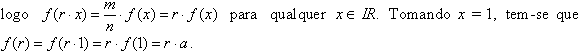
Uma
função
f
diz-se crescente quando
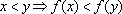 e
decrescente quando
e
decrescente quando
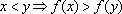 . Note que, sendo
f
crescente, vale também a
implicação oposta
. Note que, sendo
f
crescente, vale também a
implicação oposta
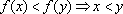 . Observação análoga para
f
decrescente.
. Observação análoga para
f
decrescente.
Teorema
1: Para todo
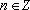 e
todos
e
todos
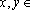 IR,
são equivalentes as seguintes afirmações a respeito de uma função
crescente
IR,
são equivalentes as seguintes afirmações a respeito de uma função
crescente
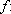 IR
IR
 IR
:
IR
:
(1)
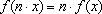 ;
;
(2)
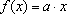 , onde
, onde
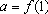 ;
;
(3)
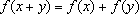 .
.
Demonstração:
Pelo Lema, pondo
a = f(1),
a afirmação (1) implica
f(r) = a . r
para
todo
x
 Q Note
que, sendo f crescente,
a desigualdade 0
< 1 implica 0
= f(0) < f(1) = a. Para provar que
(1)
Q Note
que, sendo f crescente,
a desigualdade 0
< 1 implica 0
= f(0) < f(1) = a. Para provar que
(1)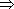 (2), suponhamos, por absurdo, que exista algum número real x
tal (2), suponhamos, por absurdo, que exista algum número real x
tal
 f(x) < ar<
ax, ou
seja,
f(x)
< f(r)
< a . x.
Sendo
f
crescente, f(x)
< f(r)
implica
x < y
, o
que contradiz
a escolha de r, pois tomamos y < x
. Partindo de (2), temos f(x + y) = a(x + y) =
ax + ay = f(x) + f(y), logo
f(x) < ar<
ax, ou
seja,
f(x)
< f(r)
< a . x.
Sendo
f
crescente, f(x)
< f(r)
implica
x < y
, o
que contradiz
a escolha de r, pois tomamos y < x
. Partindo de (2), temos f(x + y) = a(x + y) =
ax + ay = f(x) + f(y), logo
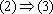 . Finalmente, supondo (3), vemos imediatamente que
f(nx)=n
. f(x)
para
todo x
. Finalmente, supondo (3), vemos imediatamente que
f(nx)=n
. f(x)
para
todo x
 IR
e
n
IR
e
n
 N. Além disso,
f(0) = f(0 +0) = f(0) + f(0), logo
f(0)=0. Daí resulta, para quaisquer n
N. Além disso,
f(0) = f(0 +0) = f(0) + f(0), logo
f(0)=0. Daí resulta, para quaisquer n
 N
e
x
N
e
x
 IR,
que IR,
que
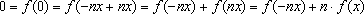 ,
,
logo
f( nx) = nx) =
 n
. f(x). Segue-se que
f(nx) =
n . f(x)
para
todo
n n
. f(x). Segue-se que
f(nx) =
n . f(x)
para
todo
n
 N e
todo
x
N e
todo
x
 IR, provando que
(3) IR, provando que
(3) 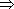 (1). (1).
Observações
1)
Evidentemente o Teorema 1 vale também para
f decrescente,
só que nesse caso
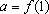 é
negativo.
é
negativo.
2)
Um corolário do Teorema 1 é que, para
f crescente
ou decrescente,
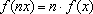 para
todo
para
todo
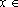 IR
e
todo
IR
e
todo
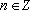 implica
implica
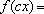
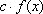 para quaisquer
c, x
para quaisquer
c, x
 IR.
IR.
3)
O número
a chama-se
constante de
proporcionalidade.
Quando
se lida com grandezas cujas medidas são números positivos, tem-se a
seguinte versão do Teorema 1:
Teorema
1+:
Para todo 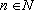 e
todos
e
todos
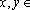 IR+
, são equivalentes
as seguintes afirmações a respeito de uma função
IR+
, são equivalentes
as seguintes afirmações a respeito de uma função
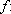 IR
+
IR
+ IR+
: IR+
:
(1)
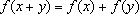 ;
;
(2)
f
é crescente e
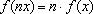 ;
;
(3)
Tem-se
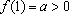 e
e
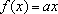 .
.
Demonstração:
A diferença agora é que, sendo positivos os valores de
f, a condição (1)
implica imediatamente que
f
é crescente. As implicações (1)
 (2)
e
(3)
(2)
e
(3)
 (1)
são imediatas. A implicação (2)
(1)
são imediatas. A implicação (2)
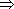 (3)
se faz nas mesmas linhas do Teorema 1 ou então observando que toda
(3)
se faz nas mesmas linhas do Teorema 1 ou então observando que toda
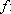 IR+
IR+
 IR+
que cumpre (2) se estende a uma IR+
que cumpre (2) se estende a uma
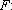 IR
IR
 IR
crescente que satisfaz o item (1) do Teorema 1: basta pôr
F(0) = 0
e IR
crescente que satisfaz o item (1) do Teorema 1: basta pôr
F(0) = 0
e
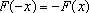 , para todo
, para todo
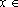 IR+.
IR+.
Observações: É inútil tentar provar que
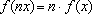 para
todo
para
todo
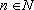 e
todo
e
todo
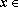 IR+
implica
f crescente.
Isso não é verdade, muito embora não seja possível apresentar um
contra-exemplo simples.
IR+
implica
f crescente.
Isso não é verdade, muito embora não seja possível apresentar um
contra-exemplo simples.
Os
teoremas 1 e
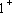 , cada um no seu contexto, determinam condições mediante as quais cabe
utilizar o modelo linear reduzido,
, cada um no seu contexto, determinam condições mediante as quais cabe
utilizar o modelo linear reduzido,
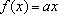 . Basta verificar que
f é crescente e cumpre . Basta verificar que
f é crescente e cumpre
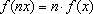 , para
, para
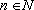 , conforme o caso.
, conforme o caso.
Exemplo
1:
Dada uma circunferência de raio
r,
seja
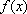 o
comprimento do arco que subtende um ângulo central de medida
x (relativamente a uma
certa unidade de ângulo). É claro que
f é
uma função crescente de
x
e que
o
comprimento do arco que subtende um ângulo central de medida
x (relativamente a uma
certa unidade de ângulo). É claro que
f é
uma função crescente de
x
e que
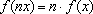 . Logo, existe uma constante
a
tal que
. Logo, existe uma constante
a
tal que
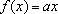 .
.
A
constante
a depende
da unidade de ângulo considerada. Se é o grau, então
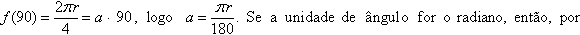 definição,
f(1) = r
, logo a
= r
. definição,
f(1) = r
, logo a
= r
.
Exemplo
2:
Ainda numa circunferência de raio
r, podemos considerar
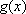 como
área de um setor circular que subtende um arco de comprimento
x. Vê-se imediatamente
que g
é uma função crescente de
x
e que
como
área de um setor circular que subtende um arco de comprimento
x. Vê-se imediatamente
que g
é uma função crescente de
x
e que
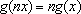 . Logo, existe uma constante
a
tal que
. Logo, existe uma constante
a
tal que
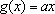 . Como o arco de comprimento
2
. Como o arco de comprimento
2 r (toda
a circunferência) corresponde ao setor de área r (toda
a circunferência) corresponde ao setor de área

A
utilização do modelo linear mais geral,
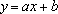 , é regida pelos teoremas seguintes:
, é regida pelos teoremas seguintes:
Teorema
2:
As
seguintes afirmações a respeito de uma função crescente
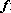 IR
IR  IR são
equivalentes:
IR são
equivalentes:
(1)
Para
todo
 IR+, o acréscimo
IR+, o acréscimo
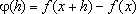 depende apenas de
h,
mas não de depende apenas de
h,
mas não de
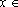 IR; com a =
IR; com a =
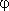 (1) = f(1) (1) = f(1)
 f(0). f(0).
(2)
Pondo
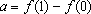 e
e
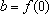 , tem-se
, tem-se
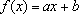 para todo
para todo
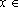 IR.
IR.
Demonstração:
Admitida a hipótese (1), definimos a função
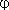 :
IR+ :
IR+  IR pondo,
para todo
IR pondo,
para todo
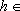 IR+,
IR+,
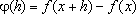 , onde
, onde
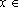 IR+ é
qualquer. Dados
IR+ é
qualquer. Dados
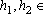 IR+, temos:
IR+, temos:
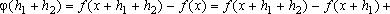
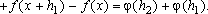
Segue-se
do Teorema
 que se tem que se tem 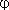 (h)
= a . h
para todo (h)
= a . h
para todo
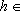 IR+,
com
a =
IR+,
com
a = 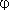 (1) = f(1) (1) = f(1)
 f(0).Conseqüentemente, para todo f(0).Conseqüentemente, para todo
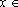 IR vale:
f(x) f(0 + x)
IR vale:
f(x) f(0 + x)
 f(0) + f(0) = f(0) + f(0) =
 (x) + f(0) = ax
+ b onde a = f(1) (x) + f(0) = ax
+ b onde a = f(1)  f(0) e b = f(0). Logo (1)
f(0) e b = f(0). Logo (1)
 ( 2). ( 2).
A implicação (2)
 (1)
é imediata.
(1)
é imediata.
Observações
1.
Em
particular, vemos que, se f é
crescente e o acréscimo
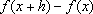 depende apenas de
h
mas não de x, então o quociente
depende apenas de
h
mas não de x, então o quociente
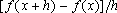 não depende de
x
nem de h.
não depende de
x
nem de h.
2.
O
Teorema 2 vale também quando f
é decrescente. A única diferença é que agora se tem
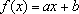 , com
, com
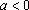 .
.
3.
Quando
as grandezas em questão só assumem valores positivos, tem-se uma função
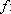 .I. .I. IR+ crescente
e a única alteração no enunciado do Teorema 2 é que, não se tendo a
priori o valor f(0),
valem IR+ crescente
e a única alteração no enunciado do Teorema 2 é que, não se tendo a
priori o valor f(0),
valem
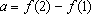 e
e
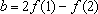 .
.
4.
Às
vezes se sabe que uma função f
é da forma
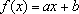 mas não se conhecem os
coeficientes a, b
nem é possível (ou conveniente) determinar
mas não se conhecem os
coeficientes a, b
nem é possível (ou conveniente) determinar
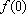 ,
,
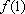 ou
ou
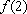 . Então basta conhecer
. Então basta conhecer
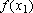 e
e
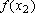 para dois valores
para dois valores
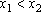 . Os coeficientes a
e
. Os coeficientes a
e 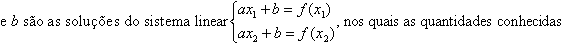 são
são
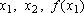 e
e
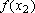 .
.
Exemplo
3:
Uma partícula se move sobre um eixo
E. (Um eixo é uma reta
orientada na qual se fixou uma origem 0. A posição de um ponto do eixo
é determinada por um número real x, chamado abcissa
desse ponto.) Em cada instante t, a abcissa do ponto é
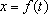 . Dizemos que se trata de um movimento uniforme quando o ponto percorre distâncias iguais em
tempos iguais. Isso significa que
. Dizemos que se trata de um movimento uniforme quando o ponto percorre distâncias iguais em
tempos iguais. Isso significa que
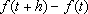 depende somente de
h
mas não de t.
A função f
é crescente ou decrescente, conforme o sentido do movimento
coincida ou não com a orientação do eixo. Segue-se do Teorema 2 que se
tem
depende somente de
h
mas não de t.
A função f
é crescente ou decrescente, conforme o sentido do movimento
coincida ou não com a orientação do eixo. Segue-se do Teorema 2 que se
tem
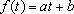 , onde
, onde
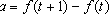 (espaço percorrido na
unidade de tempo) é, por definição, a velocidade e
(espaço percorrido na
unidade de tempo) é, por definição, a velocidade e
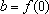 é a posição do ponto
no momento em que começou a contagem do tempo.
é a posição do ponto
no momento em que começou a contagem do tempo.
Exemplo 4:
Sejam X
e Y dois eixos que se
cortam no ponto 0, determinando assim um sistema de coordenadas (em geral
oblíquas) no plano X0Y. Seja ainda
r
uma reta não paralela ao eixo Y,
situada nesse plano. Definamos uma função
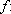 IR
IR  IR do
seguinte modo: para cada número real
x,
o valor
IR do
seguinte modo: para cada número real
x,
o valor
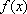 é a ordenada do ponto
é a ordenada do ponto
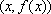 , interseção de r
com a paralela ao eixo Y
tirada pelo ponto de abcissa x
do eixo X.
Uma igualdade de triângulos evidente mostra que
, interseção de r
com a paralela ao eixo Y
tirada pelo ponto de abcissa x
do eixo X.
Uma igualdade de triângulos evidente mostra que
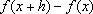 não depende de
x.
não depende de
x.
|
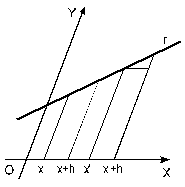
|
Portanto a função
f é do tipo
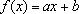 , onde
, onde
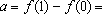
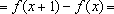
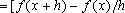 e
e
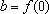 .
.
A expressão
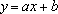 fornece portanto
a ordenada y de um ponto
fornece portanto
a ordenada y de um ponto
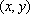 da reta r
em função da abcissa x
desse mesmo ponto.
da reta r
em função da abcissa x
desse mesmo ponto.
|
Consideremos
uma cultura de bactérias, em condições favoráveis, cuja população,
num instante t,
chamamos de
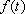 . O problema é determinar o tipo da função
. O problema é determinar o tipo da função
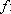 IR
IR
 IR. Ela é crescente. Mas não é razoável admitir
que
IR. Ela é crescente. Mas não é razoável admitir
que
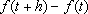 dependa apenas de
h, pois, se dependa apenas de
h, pois, se
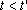 , a população
, a população
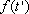 é maior do que
é maior do que
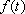 e é natural perceber
que, no mesmo período de tempo h,
o acréscimo populacional
e é natural perceber
que, no mesmo período de tempo h,
o acréscimo populacional
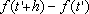 é maior que
é maior que
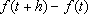 .
.
Situação
análoga ocorre com um capital aplicado a juros fixos, capitalizados
continuamente. Se
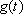 é a quantia existente
no instante t,
para t < t'
o rendimento
é a quantia existente
no instante t,
para t < t'
o rendimento
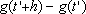 no intervalo de tempo
h é maior do que o
rendimento
no intervalo de tempo
h é maior do que o
rendimento
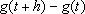 , no mesmo intervalo porém
em época anterior, pois o capital acumulado , no mesmo intervalo porém
em época anterior, pois o capital acumulado
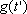 é maior do que
é maior do que
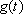 .
.
Assim,
nas duas situações acima não se aplica o modelo linear. Entretanto, se
examinarmos os acréscimos relativos
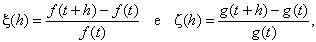
é
natural admitir que eles dependam apenas de
h, desde que, em ambas as
situações, ocorra uma certa estabilidade, ou permanência das condições
que cercam o crescimento.
No
segundo caso, o fato de que o acréscimo relativo
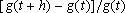 depende
apenas de
h
é a própria definição de “juros fixos”: quer dizer que, com
o passar do tempo, as condições do negócio continuam as mesmas. Quer
dizer também que o lucro obtido depois de um período de tempo fixado
h é
proporcional ao capital
depende
apenas de
h
é a própria definição de “juros fixos”: quer dizer que, com
o passar do tempo, as condições do negócio continuam as mesmas. Quer
dizer também que o lucro obtido depois de um período de tempo fixado
h é
proporcional ao capital
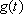 , existente no início daquele período: , existente no início daquele período:
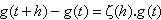 .
.
No
caso das bactérias (ou, mais geralmente, qualquer tipo de população), o
fato de que o  significa, por exemplo, que se significa, por exemplo, que se
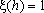 , ou seja, se
h
é o tempo necessário, a partir do instante t, para que a população duplique, então em qualquer outra ocasião
(antes ou depois) vai ser necessário o mesmo tempo
h
para que a população também duplique. Sem dúvida, essa hipótese
caracteriza uma certa estabilidade, uma permanência das condições que
cercam o fenômeno. (Que não há modificações consideráveis no meio
ambiente, que a alimentação continue existindo igualmente, etc.)
, ou seja, se
h
é o tempo necessário, a partir do instante t, para que a população duplique, então em qualquer outra ocasião
(antes ou depois) vai ser necessário o mesmo tempo
h
para que a população também duplique. Sem dúvida, essa hipótese
caracteriza uma certa estabilidade, uma permanência das condições que
cercam o fenômeno. (Que não há modificações consideráveis no meio
ambiente, que a alimentação continue existindo igualmente, etc.)
Há
diversas outras situações, em Matemática e suas aplicações, nas quais
é válida a hipótese de que o crescimento relativo:
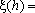
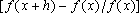
da
função
f
no intervalo
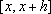 depende
do comprimento
h do
intervalo mas não do ponto inicial
x. Nesses casos, a função é determinada pelo teorema a seguir:
depende
do comprimento
h do
intervalo mas não do ponto inicial
x. Nesses casos, a função é determinada pelo teorema a seguir:
Teorema
3: Seja
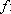 IR
IR
 IR+
uma função crescente, cujo crescimento relativo
IR+
uma função crescente, cujo crescimento relativo
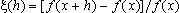 no
intervalo
no
intervalo
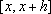 depende
apenas do comprimento
h desse
intervalo, mas não do ponto inicial. Então, pondo
depende
apenas do comprimento
h desse
intervalo, mas não do ponto inicial. Então, pondo
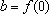 e
e
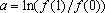 , tem-se
, tem-se
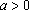 e
e
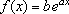 para
todo
para
todo
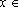 IR.
Se f
é decrescente, tem-se ainda
IR.
Se f
é decrescente, tem-se ainda
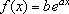 , mas,
nesse caso,
, mas,
nesse caso,
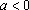 .
.
Demonstração:
Como
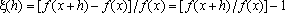 depende
apenas de
h, segue-se que
depende
apenas de
h, segue-se que
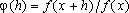 também
só depende de
h. Considerando a função
também
só depende de
h. Considerando a função
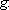 IR
IR
 IR,
definida por
IR,
definida por
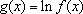 , vemos que
g
é crescente e que o acréscimo
, vemos que
g
é crescente e que o acréscimo
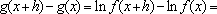
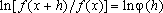 depende
apenas de
h. Pelo Teorema 2, para
todo
depende
apenas de
h. Pelo Teorema 2, para
todo
 IR
tem-se
IR
tem-se
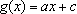 , onde
, onde
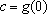 e
e
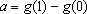 .
.
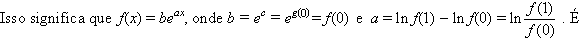 óbvio que, se
f é decrescente,
g
também é, logo óbvio que, se
f é decrescente,
g
também é, logo
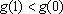 e
e
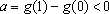 .
.
Exemplo 5:
Um corpo aquecido, quando colocado num ambiente de temperatura menor, cede
calor, portanto a diferença de temperatura
d(t),
num instante t, entre o corpo e
o ambiente, é uma função decrescente de
t. Foi observado por
Isaac Newton que, num intervalo de tempo
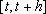 , o decréscimo relativo
, o decréscimo relativo
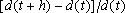 depende
apenas de
h. Daí resulta a “lei
do resfriamento, de Newton”, segundo a qual
depende
apenas de
h. Daí resulta a “lei
do resfriamento, de Newton”, segundo a qual
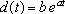 . A constante
. A constante
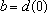 é
a diferença de temperatura no instante
é
a diferença de temperatura no instante
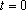 em
que teve início a experiência. Por sua vez
em
que teve início a experiência. Por sua vez
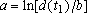 , onde , onde
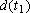 é
a diferença de temperatura medida num instante
é
a diferença de temperatura medida num instante
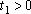 qualquer.
qualquer.
Para
encerrar, usaremos o Teorema 3 a fim de dar uma elegante caracterização
da função
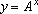 .
.
Teorema 4: Seja
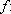 IR
IR
 IR
uma função tal que
IR
uma função tal que
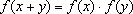 para
x, y
para
x, y
 IR.
Então, ou
f
é identicamente nula ou assume apenas valores positivos. Seja A
= f(1). Se f
é crescente, então
IR.
Então, ou
f
é identicamente nula ou assume apenas valores positivos. Seja A
= f(1). Se f
é crescente, então
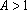 e
e
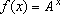 para
todo
para
todo
 IR.
Se
f é
decrescente, tem-se ainda
IR.
Se
f é
decrescente, tem-se ainda
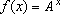 para
todo x,
mas agora
para
todo x,
mas agora
 .
.
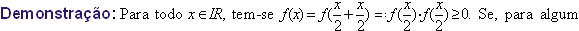
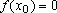 , então,
para todo
, então,
para todo
 IR,
temos
IR,
temos
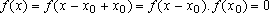 , logo
f
será identicamente nula. Assim, ou
, logo
f
será identicamente nula. Assim, ou
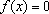 para
todo x
ou
para
todo x
ou
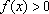 para
todo x.
Neste último caso, temos
para
todo x.
Neste último caso, temos
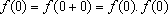 , logo , logo
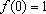 . Seja f
crescente. Como
. Seja f
crescente. Como
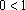 , temos
, temos
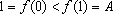 . Além disso,
. Além disso,
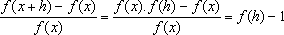
depende
apenas de
h. Segue-se do Teorema 3
que, para todo
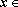 IR,
IR,
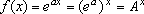 , pois
, pois
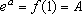 e
a constante
b
do Teorema 3 é igual a
e
a constante
b
do Teorema 3 é igual a
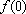 , logo vale 1.
, logo vale 1.
Corolário:
Seja
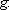 IR+
IR+
 IR
uma bijeção crescente tal que
IR
uma bijeção crescente tal que
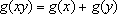 para
quaisquer
x, y para
quaisquer
x, y
 IR+.
Se
IR+.
Se
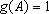 , então
tem-se
, então
tem-se
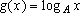 para
todo
para
todo
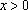 .
.
Demonstração: Basta aplicar o Teorema 4 à função
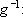 IR
IR
 IR+.
IR+.
Observações:
Na realidade, a hipótese de que
g
seja sobrejetiva é desnecessária. Basta supor
g crescente,
com
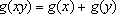 . (Ver o livro Logaritmos, do
autor, publicado pela Sociedade Brasileira de Matemática.)
. (Ver o livro Logaritmos, do
autor, publicado pela Sociedade Brasileira de Matemática.)
________________
NR:
Este artigo foi publicado na Revista
del Professor de Matemáticas, no 2,
Sociedad del
Matemática de Chile.
|