| Um
computador de papel! Existe?
|
Marcelo
Escudeiro Hernandes
Maringá, PR
|
Facilitar
cálculos sempre incentivou a pesquisa e construção de máquinas ou métodos
que diminuíssem os esforços e permitissem maior rapidez e exatidão em
operações. Assim foi com o ábaco, as barras de Napier, réguas de cálculo,
... até os computadores de hoje.
Entre
esses métodos estão os chamados nomogramas,
que são tipos de gráficos onde o resultado de operações é encontrado
utilizando uma régua ou qualquer outro instrumento que permita o traçado
de um segmento de reta.
Existem
nomogramas para operações
elementares como adição, multiplicação,
médias, hipotenusa de um triângulo retângulo e outros.
Vejamos o exemplo
de um nomograma simples para adição de dois números reais.
|
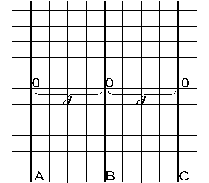
|
Tome
três eixos A, B, C,
paralelos, eqüidistantes e perpendiculares a uma reta
r
dada. Seja d
a distância entre eles. Graduamos os eixos com uma
mesma unidade e marcamos 0 nos
três eixos numa mesma horizontal. Nos eixos A
e C,
marcamos o número n (ou
-n) a n
unidades da origem. No eixo B,
marcamos 2n
(ou -
2n) a
n unidades da
origem. Veja a figura abaixo
|
|
Para
determinar a soma de dois números
a e
c,
marcamos a
no eixo A
e c
no eixo C.
A soma a + c
será determinada pela interseção da reta que une os
pontos a
e c
com o eixo B.
Veja
os exemplos:
1
+ 3 = 4
-3
+ 2
= -1
-1
+(-1)
= -2
|
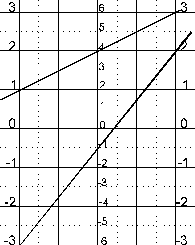
|
Por
que isso funciona? A explicação
é bem simples e pode tomar dois enfoques distintos, um algébrico e outro
geométrico. Vejamos, inicialmente, o apelo algébrico:
Suponha
que queremos encontrar a soma de dois números reais
a e c. Consideremos a
reta que passa pela origem dos três eixos como sendo o eixo x,
e o eixo B como
sendo o eixo y.
 equação é:
equação é:

Claramente,
pode-se encontrar também a diferença de dois números
e
e f, usando essa mesma construção.
Basta marcar e no eixo
B,
f
no eixo A, e ler a diferença d
no eixo C, dada
pela interseção desse eixo com a reta que passa por e e f.
De fato, teríamos f + d = e, donde,
d = e - f.
Para a
argumentação geométrica, chamemos os pontos correspondentes aos números
a
e c de
Pa
e Pc
. Observemos que há apenas três posições distintas para esses pontos:
a) Pa
e Pc estão no mesmo semiplano determinado pelo eixo x.
b) Pa
e Pc estão em semiplanos distintos em relação ao eixo x.
c)
Um argumento semelhante aos anteriores pode ser usado se um dos
pontos, Pa
ou Pc, estiver no eixo x.
|
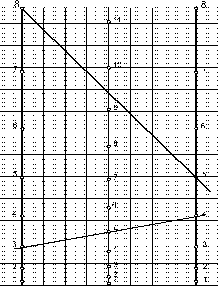
|
Vejamos a construção de
um nomograma que fornece a hipotenusa de um triângulo retângulo se forem
dados os catetos.
Como
(hip)2 = (cat1)2 +
(cat2)2, precisamos
realizar uma adição e, portanto, podemos tomar o modelo já visto. Mas,
como queremos somar quadrados de números, dessa vez
nos eixos A
e C
escrevemos o número n
a n2 unidades
da origem e no eixo B escrevemos o número n
a n2/2
unidades da origem.
Aos
catetos 3 e 4 corresponde a hipotenusa
5 e aos catetos
8 e
5 corresponde a hipotenusa
»
9,4
|
|
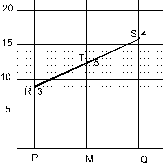
|
Detalhando:
PR tem 9 unidades;
a R corresponde ao número 3.
QS tem 16 unidades;
a S corresponde o número 4.
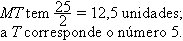 |
Para a
multiplicação de dois números positivos pode-se usar novamente o mesmo
tipo de nomograma, lembrando que, se
x . y = z,
então log x + log y = log z
, qualquer que seja a base do
sistema de logaritmos. Nesse
caso, para marcar os números nos eixos A
e C , fixamos a origem em
cada eixo e marcamos o número n
a uma distância igual a log
n unidades dessa origem. No
eixo B marcamos
o número n a uma distância igual a
1/2 log n
unidades da origem.
Uma figura, praticamente igual à de cima, mostrará por que tal
nomograma funciona.
|
NOTA
HISTÓRICA
(de
autoria de
José Paulo Carneiro)
|
Gráficos
como os apresentados neste artigo, ou nomogramas, destinam-se a calcular
valores de funções ou resolver equações, através do traçado apenas
de retas.
Embora seus princípios básicos estejam implícitos em diversos
instrumentos imaginados na antiguidade para resolver problemas isolados, o
estudo sistemático de nomogramas surgiu em 1885, com C.
Lallemand e principalmente com Maurice
d’Ocagne, que criou o termo “Nomografia” (M. d’Ocagne, Nomographie.
Les calculs usuels effectués au moyen des abaques,
Paris, 1891). Nos livros de língua inglesa, os nomogramas são
conhecidos também como allignement
charts. Até menos de meio século atrás, o estudo dos métodos da
Nomografia (assim como do uso da “régua de cálculo”, baseada em
princípios semelhantes) fazia parte de um curso padrão de Cálculo
Numérico, nos cursos técnicos das Universidades. Embora superados, em
termos práticos, pelos computadores, os nomogramas constituem ainda
instrumentos interessantes do ponto de vista didático. O leitor
interessado pode consultar, por exemplo, o
livro de J. Lipka, Graphical and Mechanical Computation,
New York, 1918.
|
 |
|
Marcelo
Escudeiro Hernandes
é licenciado pela Universidade Estadual de Maringá, onde
atualmente leciona como professor auxiliar, e mestrando em Matemática
pelo ICMSC. |
|
 |
|