|
Flávio Wagner Rodrigues
IME-USP
Soluções e Sugestões:
RPM - Problemas
Caixa Postal 66281
05389-970 São Paulo, SP |
 |
130. Utilizando apenas uma régua (sem escala) que
permite traçar paralelas, determinar o ponto médio de um segmento dado.
Justificar.
(Sugerido por Paulo Ferreira Leite, São Paulo, SP.)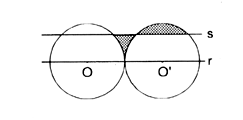
131. Na figura temos dois círculos de mesmo raio,
com centros em O e O', tangentes entre si.. Calcule a distância
entre as retas paralelas r e s de modo que as duas regiões
hachuradas tenham a mesma área. (Enviado por Regis Sant 'Ana,
PR.)
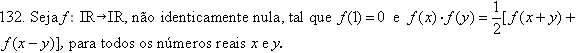
a) Mostre que f(0)
= 1; f(2) =
 1;
f(3)=0 e
f(4) = 1. 1;
f(3)=0 e
f(4) = 1.
b) Mostre que f (x + 4) = f(x)
, para todo x real.
c) Existe, de fato, uma tal função?
Sugestão: Tente encontrar uma função trigonométrica verificando as condições
dadas.
(Proposto por Cláudio Arconcher, Jundiaí, SP.)
133. Oito times disputam a inclusão no quadrangular final de um campeonato de
futebol. Sabe-se que cada par de times joga uma só vez entre si e que, em caso
de vitória, o time ganha dois pontos, no caso de empate, ganha um ponto e, na
derrota, não ganha ponto. Qual é o número mínimo de pontos que um time deve
alcançar para garantir a passagem para o quadrangular final? [Do
livro Olimpíadas de Matemática do Rio de Janeiro (veja p. 55 nesta RPM).]
1. Uma pessoa, escrevendo a sucessão dos números
naturais (começando pelo zero), interrompeu seu trabalho em um certo número.
Qual é esse número se, até parar, a pessoa escreveu 7 350 algarismos?
(Enviado por Max Denis de L. Santos, Maceió, AL.)
2.
Considere uma ampulheta (relógio de areia) formada por dois cones iguais de 12
cm de altura. Suponha que o cone superior, completamente cheio de areia na hora
zero, se esvazia em 24 horas. Qual é a hora do dia no momento em que a altura da
areia, no cone superior, é metade da altura desse cone?
(Da revista El Acertijo, n° 19 — Buenos Aires, Argentina.)
3. Escreva nas
casas vazias algarismos de l a 8 de modo que as igualdades se verifiquem, no
sentido das flechas.
(Da revista El Acertijo, n° 19.)
(Ver
respostas no
final desta
seção
)
|
 |
| Soluções dos
problemas propostos na RPM 28 |
722. Entre todos os triângulos de lados inteiros
que têm um dos ângulos igual ao quíntuplo de um outro, determine aquele que tem
os menores lados possíveis.
Solução:
 Pela
lei dos senos, tem-se Pela
lei dos senos, tem-se
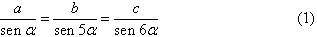
Através das
fórmulas das funções trigonométricas da soma de arcos, obtém-se:

Pela lei dos cossenos conclui-se que cos é racional. Assim, 2 cos
é racional. Assim, 2 cos = p/q , com p e q inteiros e sem fatores comuns. Portanto,
= p/q , com p e q inteiros e sem fatores comuns. Portanto,
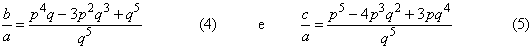
Os
menores lados inteiros que satisfazem (5) são a = q5
e c = p5
 q2(4
p3 q2(4
p3
 3pq2)
. De fato, se esses números admitissem um fator comum, que podemos supor
primo, então p e q não seriam primos entre si. Logo, de (4) temos: b=
p4q 3pq2)
. De fato, se esses números admitissem um fator comum, que podemos supor
primo, então p e q não seriam primos entre si. Logo, de (4) temos: b=
p4q
 3p2q3
+ q5. 3p2q3
+ q5.
Como 0°< 6 <180°, tem-se 0°<
<180°, tem-se 0°<
 <30° e,
conseqüentemente, <30° e,
conseqüentemente,
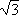 < p/q <
2 . A fração de menor denominador que satisfaz essa inequação é p/q =
7/4, que leva a a = 1024, b=1220
e c = 231. < p/q <
2 . A fração de menor denominador que satisfaz essa inequação é p/q =
7/4, que leva a a = 1024, b=1220
e c = 231.
Observamos ainda
que, para q
 5,
temos a = q5 5,
temos a = q5
 3125. Se 0° <
3125. Se 0° < 
 18°
, então sen 5 18°
, então sen 5 >sen
>sen , já que a função seno é crescente no 1.° quadrante Se 18° <
, já que a função seno é crescente no 1.° quadrante Se 18° <

 30°, então a desigualdade também se verifica, pois sen 5
30°, então a desigualdade também se verifica, pois sen 5 > 1/2 > sen
> 1/2 > sen  . Portanto, através de (l) , temos b>3125.
Finalmente,
. Portanto, através de (l) , temos b>3125.
Finalmente,
c
= p5
 4p3q2 + 3pq4 = p (p4
4p3q2 + 3pq4 = p (p4
 p2q2
p2q2
 3p2q2 + 3q4) =
3p2q2 + 3q4) =
= p[p2(p2-q2)
 3q2(p2
3q2(p2
 q2)] = p(p2
q2)] = p(p2
 3q2)(p2 3q2)(p2
 q2),
q2),
e p2
 3q2
é positivo e inteiro (p2 3q2
é positivo e inteiro (p2
 3q2 3q2
 l),
logo, l),
logo,
c
 p(p2
p(p2
 q2) >
q2) >
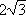 q3
> 400. q3
> 400.
Portanto o triângulo encontrado "tem os menores
lados possíveis".
Obs.: O problema original, enviado com solução por Rubem Alva Cabrera, é
mais geral substituindo no enunciado "quíntuplo" por "múltiplo".
123. Na figura
AD=BC. Determine o ângulo BCD.

Solução:
Construimos o triângulo equilátero ACE. Os
triângulos BCE e ACD são congruentes, pois CE=AC,
 BCE = BCE =
 DAC = 100° e
BC = AD. DAC = 100° e
BC = AD.
Logo , -
 BEC = 40 +
x. Como o triângulo ABE é isósceles, então BEC = 40 +
x. Como o triângulo ABE é isósceles, então
 AEB = 10° e,
portanto, x=10°, AEB = 10° e,
portanto, x=10°,
[Solução enviada por Paulo Roberto
Furtado Dias, RJ.]
124. São dadas duas progressões aritméticas
distintas cujos termos são números inteiros positivos. Determine condições que
devem ser satisfeitas para que existam termos comuns às duas progressões.
Solução:
Sejam (a1,r) e (a'1,r')
as duas progressões. Se a1 = a'1,
as duas progressões terão termos em comum. Vamos supor, sem perda de
generalidade. que a1 > a'1.
Para que existam termos em comum é necessário que existam inteiros positivos
m e n tais que a1+ nr = a'1+
mr'. Portanto, o, a1
 a'1
= mr' a'1
= mr'
 nr .
Para que existam soluções inteiras, é necessário que a1 nr .
Para que existam soluções inteiras, é necessário que a1
 a'1
seja múltiplo do máximo divisor comum de r e r'. a'1
seja múltiplo do máximo divisor comum de r e r'.
[Adaptado da solução enviada por João Linneu do Amaral
Prado, SP.]
125. Determine um polinômio P(x), com coeficientes
inteiros, tal que x0 =
 seja uma raiz
da equação P(x) = 0 . Resolva a mesma questão para x1
= seja uma raiz
da equação P(x) = 0 . Resolva a mesma questão para x1
=  . .
Solução:
Primeira
parte: x
 1 = 1 =

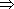 (x (x
 1)3
= 5 1)3
= 5 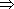 x x
 3x2
+ 3x 3x2
+ 3x  l
= 5 . Donde segue que o polinômio procurado é P(x) = x l
= 5 . Donde segue que o polinômio procurado é P(x) = x
 3x2
+ 3x 3x2
+ 3x  6. 6.
Segunda parte:

[Solução enviada por vários leitores.]
|
Relação dos leitores
que enviaram soluções dos problemas 122 a 125 da RPM 28 |
|
Alceu de Amorim Ramos (SP) - 123 |
José Henrique Piccirillo (SP) - 123 |
|
Alex Pereira Bezerra (PE) - 123 |
José Hemandez (SP) - 123, 25 |
|
Amadeu C. de Almeida (RJ) - 123, 25 |
José Renato C. e Carneiro (SP) - 125 |
|
Antonio Ferreira Sobrinho (SP) - 123 |
Josivan Araújo da Silva (PB) - 123, 25 |
|
André L. C. dos Santos (RJ) - 124, 25 |
Luis Lopes (Canadá) - 123, 25 |
|
Carlos A. da S. Vitor (RJ) - todos |
M. Ivete Cardano Rodrigues (SP) - 123 |
|
Cid Carlos Leite da Silva (AL) - 123 |
Miguel de C. Neves (RJ) - 123, 24, 25 |
|
Douglas Rosseto (SP) - 123 |
Paulo Roberto Furtado Dias (RJ) - 123 |
|
Evandro Freitas (RJ) - 123 |
Paulo Sérgio da C. Lino (MG) - 123, 25
|
|
Fernando Seiti Goto (SP) - 123 |
Pierre Bedouch (MG) - 123, 25 |
|
F. W. Leão (RJ) - 123 |
Régis Sant'Ana (PR) - 123, 24, 25 |
|
Geraldo Perlino Jr. (SP) - todos |
Ricardo da Silva Rabello (DF) - 124, 25 |
|
Janilson Aparecido Balieri (MG) - 123 |
Roberto A. Loewenborg (SP) - 125 |
|
João Batista de Araújo F. (MG) - 123 |
Rúben Alva Cabrera (Peru) - 122, 23 |
|
João Lineu do A. Prado (SP) - 124, 25 |
Sérgio Dalmas (SC) - todos |
|
José B. de Carvalho (PE) - 123 |
Tsunediro Takahashi (SP) - 123, 25 |
|
Reposta dos
probleminhas (p. 43) |
|
(1) 214
(2) 21 horas |
(3) Começando no canto superior esquerdo
e girando no sentido anti-horário: 6,3,2,4,8,7,1,5. |
|
|