|
Matemática – conceitos e operações
5.ª série do 1.° grau
Scipione de Pierrô Netto
Editora Saraiva
|
Gita k.
Ghinzberg
Colégio I. L.
Peretz
São Paulo, SP. |
Há muitos anos temos indicado e
utilizado como livro texto nas nossas classes de 5ª série do 1º grau o
volume de Scipione de Pierrô Netto – Matemática – Conceitos e Operações – da
Editora Saraiva. Este volume contém as seguintes unidades: primeiras idéias
sobre conjuntos; o conjunto dos números naturais; operações em N;
múltiplos e divisores; o conjunto dos números racionais; números decimais;
Geometria intuitiva e sistema métrico decimal.
A escolha deste livro para os nossos
alunos de 5.ª série teve a vantagem de possibilitar uma continuidade e um
aprofundamento dos tópicos já iniciados nas 4 primeiras séries do 1.° grau
e, nas palavras do próprio autor “visa desenvolver procedimentos que
possibilitem a conquista dos princípios de generalização”.
Trata-se de um livro bastante rico na
quantidade de exercícios, facilitando o trabalho do professor que pode
encontrar aí um apoio efetivo no sentido de proporcionar aos seus alunos um
treino no tocante às operações no conjunto dos naturais e dos racionais e no
cálculo com o sistema métrico decimal.
O treino, entretanto, embora
importante, não satisfaz os objetivos de um professor voltado ao
desenvolvimento de seus alunos. O excesso de padronização dos exercícios e
problemas, fato comum em quase todos os livros didáticos, desestimula tanto
o aluno que julga ter dificuldades quanto aquele que não as tem. A inclusão
de problemas e exercícios não padronizados, mais criativos, que estimulem a
vontade de resolvê-los, bem como o prazer de raciocinar, completaria o
volume na sua finalidade pedagógica.
Como sabemos, nas classes de 5.ª
série, em geral, cabe ao professor a explicitação dos conceitos através do
que a maioria dos nossos alunos denomina de “ponto de Matemática” e que
anota em seus cadernos. Essa tarefa de explicação para a sedimentação dos
conceitos é função própria do professor e não elimina o livro-texto. Mas,
dificilmente, encontraremos o livro utilizado como ferramenta para a
aprendizagem, em especial, na 5,ª série, onde a faixa etária de um lado e a
falta de hábito, de outro, constituem os principais impecilhos.
Cabe examinar como esse livro se
apresenta para o professor e para o aluno:
O livro de Scipione de Pierrô Netto, é
impresso em mais de uma cor e é agradável à vista, mas na sua parte
conceitual é comparável à maioria dos livros didáticos em circulação. Contém
o suficiente. O professor mais exigente se ressente não só de uma
bibliografia, de apêndices esclarecedores ou de aprofundamento teórico, de
anotações da História e da evolução da Matemática, mas também da sua
aplicação concreta na vida cotidiana dos alunos. Esses aspectos, se
existentes, tornariam esse livro mais atraente e mais objetivo
transformando-o em um manual mais eficiente tanto para o professor quanto
para o aluno.
O capítulo dedicado aos sistemas de
numeração, por exemplo, cuja importância nos dias de hoje será redundante
ressaltar, está ilhado no conjunto do livro, pois não encontra também
aplicações nos capítulos subseqüentes, perdendo toda a finalidade como
aprendizagem.
Estas considerações, sem dúvida, se
aplicam também à maioria dos livros didáticos utilizados pelos nossos
alunos. O replanejamento dos compêndios de modo a torná-los mais
interessantes e eficazes no processo de aprendizagem deveria ser uma tarefa
de nossos autores, editores e autoridades de ensino.
|
Problemas de Matemática Elementares
V.
Lidsky e outros
Editora Mir
Distribuidoras: “Livraria Tecno-Científica”; Rua Barão de Itapetininga
88, Galeria Ita – Loja 6A; 01042 São Paulo, SP
“Livraria página Ltda.”; Rua das Marrecas, 40 – 5.º/511 Rio de Janeiro,
RJ |
Renate Watanabe
|
Trata-se, como diz o título, de um
livro de problemas.
São problemas que só exigem
conhecimentos a nível do 2.º grau mas, por suas dificuldades, destinam-se a
alunos e professores interessados em “algo mais” do que normalmente é
apresentado na escola. O livro é especialmente recomendável para estudantes
e professores que desejam participar de Olimpíadas de Matemática ou para
aqueles que sentem prazer em resolver problemas não triviais.
O livro contém 658 problemas: a sua
apresentação ocupa as primeiras 80 páginas, as soluções ocupam as 300
páginas restantes, sendo o livro, por isso, também um manual de estudo.
Os problemas abrangem tópicos de
Álgebra, Geometria e Trigonometria.
Cada tópico é precedido de uma página
contendo as principais fórmulas e algumas explicações sucintas. O nível dos
problemas é melhor descrito através de alguns exemplos:
16.
Determine a soma 1 + 11 + ... + 111 .... 1, sabendo-se que a última
parcela é um número de n algarismos.
111. Demonstre: 1/a + 1/b + 1/c
³ 9/(a + b + c), sendo a, b e c números positivos.
346. Em um triângulo isósceles
de base a e lados congruentes iguais a b, o ângulo oposto à
base mede 20º. Demonstre que a3 + b3 = 3ab2.
532.
Uma pirâmide triangular é interceptada por planos paralelos a duas
arestas que não têm ponto comum. Determine a secção de maior área.
É pena que o livro não exista em
Português. As versões em Espanhol e Inglês podem ser encontradas nas
livrarias mencionadas. Em agosto de 1983 os preços eram: Cr$. 2.700,00 (em
espanhol) e Cr$. 1.960,00 (em inglês).
As soluções dos problemas são, em
geral, claras e suficientemente detalhadas para fácil compreensão.
|
Respostas dos ...probleminhas |
|
 |
 |
|
3. 5 minutos
4. 1/4 para filha
1/4 para neta
1/2 para o neto |
|
Euler e os símbolos que usamos |
|
EULER foi um grande construtor de notações,
isto é símbolos matemáticos, que hoje usamos sem questionar sua origem.
Eis alguns exemplos: p (1737) (letra inicial de perímetro e periferia em
grego: respectivamente 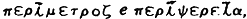 (1731,36),
(1731,36),  (1777, publ. 1794).
Na verdade além de e (1777, publ. 1794).
Na verdade além de e  (1755), e ex, log x, sen x, cos x. (De fato, sin e cos como
abreviações de sinus e cosinus, do latim). Também A, B, C, e a, b, c
para os ângulos e lados de um triângulo e s para a semi-soma desses
lados. Todas são notações de EULER.
(1755), e ex, log x, sen x, cos x. (De fato, sin e cos como
abreviações de sinus e cosinus, do latim). Também A, B, C, e a, b, c
para os ângulos e lados de um triângulo e s para a semi-soma desses
lados. Todas são notações de EULER.
G. M. de
La Penha |
|