- Um leitor de Jataí, GO, pergunta sobre Diofante.

RPM: Pouco se sabe sobre a vida do grego Diofante. Crê-se que tenha vivido em Alexandria, por volta de 250 d.C. Sua grande obra, Arithmetica, tem 6 volumes preservados, mas acredita-se que foi escrita em 13 volumes.

Quanto ao seu trabalho matemático, destacamos alguns pontos interessantes:

   Embora escrita em grego, sua obra não apresenta as mesmas características dos trabalhos gregos do período - por exemplo, seu enfoque na Álgebra, incipiente na Matemática grega da época, ou, ainda, sua não-preocupação com métodos gerais. Assim, a resolução de equações indeterminadas do tipo   Ax²+ Bx + C = y²,  ou   Ax³ + Bx² + Cx + D = y²,   consistia em obter    uma   solução e não se preocupar com as demais. Entre as equações que estudou estão, por exemplo,   x² 26y² = 1   e   x² 30y² = 1,   hoje conhecidas como equações de Pell.

   Diofante só se interessava por soluções racionais positivas, não aceitando as negativas ou as irracionais.

   Na obra de Diofante encontramos pela primeira vez o uso sistemático de símbolos algébricos. Equações algébricas são expressas por símbolos algébricos e seu tratamento é puramente analítico, desvinculado de métodos geométricos. Identidades como (a + b)² = a² + 2ab + b², que, para Euclides, eram teoremas da Geometria, para Diofante eram conseqüências imediatas das propriedades algébricas das operações.

   Diofante era muito hábil no manuseio algébrico. Por exemplo, para calcular dois números, sabendo que a sua soma é 20 e a soma de seus quadrados é 208, ele representava esses números por   10 x   e    10 + x   e não por   x e y.    Tal procedimento, em muitos casos, simplificava a resolução de um problema.

   Outro problema abordado por ele:  dividir um quadrado em dois quadrados, isto é, encontrar inteiros  a, b e c tais que  a² + b² = c²,   parece ter despertado a atenção de Fermat, que, ao ler a cópia do livro de Diofante, fez diversas anotações nas margens, entre elas o famoso "último teorema de Fermat" (v.   RPM 15, p. 14 e nesta revista p. 20).

   Os problemas estudados por Diofante são problemas indeterminados que exigem soluções inteiras (ou racionais) positivas e envolvem, em geral, equações de grau superior ao primeiro. Mesmo assim, hoje em dia, equações indeterminadas do primeiro grau, com coeficientes inteiros, são chamadas equações diofantinas em homenagem ao pioneirismo de Diofante nessa área.

   A título de curiosidade, reproduzimos um problema que apareceu sob forma de poema no quinto ou sexto século.   Ele permite calcular quantos anos Diofante viveu:

Diofante passou 1/6 de sua vida na infância, 1/12 na juventude e mais 1/7 antes de se casar; 5 anos após seu casamento, nasceu um filho que morreu 4 anos antes do pai com a metade da idade que este tinha ao morrer.

(Para redigir essa resposta, e por estarem à mão, os seguintes livros foram consultados:

[1]  BOYER, C.B. História da Matemática. São Paulo, Edgar Bliicher, 1974.

[2]  CAJORI, F. A history of Mathematics. 2. ed. New York, Macmillan, 1919.

[3]  MONTEIRO,  L.H.J.  Elementos de Álgebra.     Rio de Janeiro,   Ao  Livro Técnico, 1969. [4]  STRUIK, D.        J. A concise history of Mathematics.    London, G.  Bell and Sons. 1954. )

- Um leitor de Valença, RJ, quer saber qual a taxa de juros embutida na seguinte situação:

Um CD custa R$23,00 à vista, mas pode ser pago em 3 prestações de R$10,00, uma de entrada, uma em 30 dias e outra em 60 dias.

RPM:   Cuidado ao fazer compras — a taxa de juros embutida em pagamentos parcelados pode ser muito elevada! Veja corno proceder:

Supondo juros simples, faça a seguinte conta:

    você paga   R$10,00   no ato da compra e fica devendo   R$13,00;

    esses   R$13,00,   após 60 dias, transformam-se em   R$20,00;

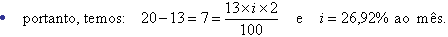
Supondo juros compostos, a conta fica:

    você paga   R$10,00   no ato da compra e fica devendo   R$13,00;

    e tem que pagar  R$10,00;   portanto,

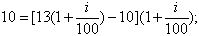
  calculando o valor de   i,   chega-se a     i 34,15%   ao mês.

Para explicações mais detalhadas, veja RPM 8, p. 11, RPM 20, p. 23 ou RPM 22, p. 13.

- Uma leitora de Sobradinho, DF, quer saber a origem das palavras cateto e hipotenusa.

RPM:   Ambas vêm do grego:

     cateto vem de kátetos e quer dizer "vertical" ou "perpendicular";

     hipotenusa vem de hypoteínousa e significa "linha estendida por
baixo".

Não localizamos nenhum outro fato ligado a essas palavras. Algum leitor teria maiores informações?