|
De Grão em Grão... |
Enviado por
Rosalina B. de M. Miranda,
Estrela
d'Oeste, SP
|
Carlos Eduardo Alves Pereira,
aluno da E. E. Sílvio Miotto, em
Estrela d'Oeste, participou da fase final da 15.ª
Olimpíada de Matemática
do Estado de São Paulo, realizada em 1991, quando cursava a 8.ª
série.
Ele é meu aluno e quando estava na 7.ª
série montou, de um
modo bastante interessante, uma tabela para o número de diagonais de um
polígono em função do número de lados.
|
Partindo do triângulo, que não tem diagonais, ele
chegou ao polígono de 100 lados e não
precisou fazer cálculos muito
complicados, pois percebeu que,
enquanto o número n
de lados cresce uma unidade, o número de diagonais dn
cresce esse número de lados menos um. E construiu a tabela, da qual reproduzo um trecho. |
n |
dn |
|
|
|
3 |
0 |
|
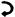
+2 |
|
4 |
2 |
+3 |
|
5 |
5 |
+4 |
|
6 |
9 |
+5 |
|
7 |
14 |
+6 |
|
... |
|
|
|
99 |
4752 |
 |
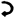+98 |
|
100 |
4850 |
|
RPM: Com efeito, o número dn de diagonais se escreve
como um polinômio do
2.° grau em n. A diferença entre dois
polinômios
será um polinômio do 1.°
grau, cujos valores formarão uma progressão
aritmética se os acréscimos dados a n forem constantes. Ou seja,
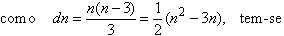
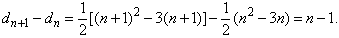
Um outro modo de ver isso é destacar um vértice P do polígono
de n + 1 lados e considerá-lo como um polígono de n lados ao qual
se justapõe um triângulo, como ilustram as figuras.
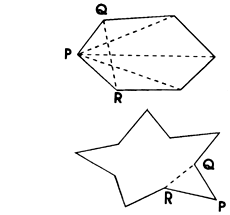 Às diagonais do polígono de n lados é preciso acrescentar as n
 2
diagonais que saem de P e, ainda,
RQ,
que é um lado do polígono de
n
lados e passa a ser
diagonal no polígono de n + 1 lados. Ao todo, acrescentam-se
n
1 diagonais.
Como será que Carlos Eduardo chegou ao seu modo de construir a
tabela? Só perguntando a ele.
|
