|
Explorando o Sistema de
Numeração
Decimal
para o
Cálculo da Raíz Quadrada
por Tentativas
A colega Rosaly Mara S. Garita, de Botucatu, SP, envia-nos
trabalho de alunos seus, Márcia Maria Quinelato dos Santos (8.ª série), Wesley Patryck Dultra de Almeida e André Ricardo Bardella Diez (7.ª série)
em que eles acham raízes quadradas por meio de tentativas.
|
1 - Cálculo de raízes exatas |
Para encontrar  , por exemplo, eles começam por
encontrar o algarismo das dezenas da raiz. Este deve ser 1 porque 10
x
10 = 100 é menor do que 324, enquanto 20
x
20 = 400 é maior do que 324. Para encontrar o algarismo
das unidades, eles procuram entre aqueles cujo quadrado termine em 4, como
324. Então poderia ser
2 ou 8. Reduzem, desta forma, as tentativas a 12 e a
18. Sendo
12 x 12 = 144
 324, a raiz procurada deve ser
18, o que de fato se verifica pois, 18
x 18 = 324.
|
2 - Cálculo de raízes inteiras aproximadas |
Para encontrar  , em que o algarismo da dezena deve também ser 1, eles iniciam as tentativas com 9 no algarismo das unidades,
pois 20 x 20 = 400 está muito mais próximo de 388
do que 10 x 10 = 100. E, como 19 x 19
= 361, a raíz aproximada será 19.
|
3
- Cálculo de raízes aproximadas, com erros menores do que
0,1 ou 0,01 ou
... |
Seja, por exemplo, o problema de calcular
 , com erro menor do que 0,1. Basta
aplicar o processo anterior ao número 13
x
102 =
1.300 e multiplicar a raiz obtida por 0,1. Mas o algarismo das dezenas na
deve ser 3 e, como
30
x 30 = 900
e
40
x 40 = 1.600, é este que
está mais próximo de 1.300. Então iniciaram suas tentativas partindo de 39x39=1.521, que é muito grande ainda, bem como
38 x 38 = 1.444 ou 37
x 37 = 1.369. Como 36
x 36=1.296, a raiz procurada será
3,6.
Analogamente, calcularam
 com erro inferior a 0,1, verificando que o algarismo das dezenas de
 deve ser 6 e, como 60
x 60 = 3.600 está perto de 3.800, tentaram 61x61=3.721, donde
 =
6,1....
N.R. Estas observações de proximidade tornam o processo de tentativas mais rápido. Um modo de "cercar" melhor o número que se
procura é tentar o ponto médio. No cálculo de
 , por exemplo, em que
302 e 402 são quase eqüidistantes de 1.300, seria o caso de tentar 35
x 35 = 1.225, que ainda é menor e, então, tentar 36
x 36, que é o número procurado.
|
Respostas dos probleminhas |
|
1.
Antes de sair, dei corda no relógio de parede sem me
preocupar em acertá-lo. Anotei a hora A que ele marcava quando saí. Na
casa do meu amigo anotei as horas exatas h e
k, respectivamente,
da minha chegada e da minha partida. Chegando em casa, anotei a hora
B
que meu relógio marcava. B  A é o tempo que fiquei fora;
k h é o
tempo que fiquei na casa do meu amigo; t é o tempo gasto para ir de
minha casa à do meu amigo. Então B
A
=
2t +
k
h, de onde se tira o valor
de t. A hora certa, no momento de chegada, é
k + t.
|
2.
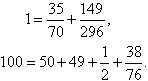
4. No fim de 6 jogadas, em
qualquer caso, você estará com Cr$ 67,50.
|
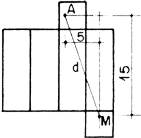
3. d2 = 52
+ 152; d
15,81.
 |
|
|
