|
(transcrição adaptada da Nota da Redação publicada na RPM 2, p. 27)
Há, em
geral, duas preocupações em relação ao algoritmo para o cálculo de raízes
quadradas: 1.°)
o aluno aprende os passos sem
entendê-los, 2.°)
o aluno facilmente se esquece desses passos.
Com
efeito, embora o cálculo da raiz quadrada ocorra com bastante freqüência
em problemas de Geometria, de Mecânica, etc, a maioria das pessoas (mesmo
matemáticos profissionais), tendo aprendido tal algoritmo na escola,
esquece-o pouco depois.
|
Ora, mais importante do que isto é
a questão de saber se se deve ensinar a extração de raízes quadradas
usando o algoritmo tradicional. |
|
Há vários
outros meios de extrair a raiz quadrada que dificilmente podem ser
esquecidos, pois exigem bem menos da nossa memória. |
Citamos os
seguintes:
1. O
MÉTODO DAS TENTATIVAS. É o mais rudimentar, que funciona bem para números
com poucos algarismos decimais. Para números mais longos, deve ser
complementado por uma calculadora (no que é superado pelo método 4). Ele
opera assim: suponhamos que
se quer calcular
 . É claro
que 32 < 10 < 42, logo . É claro
que 32 < 10 < 42, logo
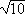 = 3,
....
Além
disso, (3,1)2 < 10 < (3,2)2, logo = 3,
....
Além
disso, (3,1)2 < 10 < (3,2)2, logo
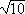 =
3,1.... Por tentativas, verificamos também que (3,16)2
< 10 < (3,17)2, logo =
3,1.... Por tentativas, verificamos também que (3,16)2
< 10 < (3,17)2, logo
 = 3,16....E assim por diante. = 3,16....E assim por diante.
2. O
MÉTODO DAS APROXIMAÇÕES SUCESSIVAS (v. p. 13 nesta RPM e, também,
RPM 9,
pp. 65 e 66; Análise Real, vol. 1, p. 30, publicação da
SBM).
Para obter  , começamos com uma primeira aproximação
a1, escolhida experimentalmente.. A menos que n seja um
quadrado perfeito (o que não é comum) tem-se, em geral, a1 , começamos com uma primeira aproximação
a1, escolhida experimentalmente.. A menos que n seja um
quadrado perfeito (o que não é comum) tem-se, em geral, a1

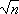 . Então um
dos dois números a1, n/a1 é menor do que . Então um
dos dois números a1, n/a1 é menor do que
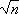 e o outro
é maior. Se a escolha inicial a1 for maior do que e o outro
é maior. Se a escolha inicial a1 for maior do que
 ou se
não for demasiadamente menor do que ou se
não for demasiadamente menor do que
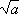 , então a média , então a média

3.
TABELAS. Se temos uma tabela de raízes quadradas, basta olhar. Caso
contrário, podemos lançar mão de uma tábua de logaritmos, que é bem mais
fácil de
encontrar. A 
4.
CALCULADORA. Quase todas as calculadoras têm uma tecla sobre a qual está
escrito  . Basta
registrar o número n e apertar essa tecla para
obter a raiz quadrada de n. . Basta
registrar o número n e apertar essa tecla para
obter a raiz quadrada de n.
Cada um dos métodos acima, bem como o
método tradicional, tem seus prós p seus contras. Por exemplo, o método 4 é sem dúvida o mais eficiente,
mas tem a desvantagem de exigir uma maquininha com as pilhas carregadas. (Seus
defensores podem contra-argumentar: "Mas isso todo mundo tem. Quem haveria
de querer calcular 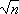 numa ilha deserta?".) O método 3 também não
funciona numa ilha deserta: ele depende de termos um certo livro disponível.
Em compensação, usando logaritmos podemos calcular, com a mesma facilidade,
não somente raízes quadradas como raízes cúbicas, quartas, etc. Para tais
raízes de índice maior do que 2 já seria necessária uma maquininha mais
cara. Os métodos 1 e 2 independem de tabelas ou máquinas, mas são mais
trabalhosos do que o método tradicional, principalmente para números com
muitos algarismos. Finalmente observamos que, do ponto de vista conceituai,
o método 2 (das aproximações sucessivais) é o mais simples e elegante de
todos. Além disso, ele se estende facilmente para raízes n-ésimas e mesmo
para raízes de uma equação algébrica, sob a forma conhecida como método de
Newton (v. RPM 4, p. 25; Análise Real, vol. 1, pp. 112 a 116). O
método de Newton, do qual o método 2, acima, é um caso particular,
apresenta a enorme vantagem de ter "convergência quadrática". No nosso caso,
isto significa que o erro cometido em cada etapa é aproximadamente o
quadrado do erro da etapa anterior. numa ilha deserta?".) O método 3 também não
funciona numa ilha deserta: ele depende de termos um certo livro disponível.
Em compensação, usando logaritmos podemos calcular, com a mesma facilidade,
não somente raízes quadradas como raízes cúbicas, quartas, etc. Para tais
raízes de índice maior do que 2 já seria necessária uma maquininha mais
cara. Os métodos 1 e 2 independem de tabelas ou máquinas, mas são mais
trabalhosos do que o método tradicional, principalmente para números com
muitos algarismos. Finalmente observamos que, do ponto de vista conceituai,
o método 2 (das aproximações sucessivais) é o mais simples e elegante de
todos. Além disso, ele se estende facilmente para raízes n-ésimas e mesmo
para raízes de uma equação algébrica, sob a forma conhecida como método de
Newton (v. RPM 4, p. 25; Análise Real, vol. 1, pp. 112 a 116). O
método de Newton, do qual o método 2, acima, é um caso particular,
apresenta a enorme vantagem de ter "convergência quadrática". No nosso caso,
isto significa que o erro cometido em cada etapa é aproximadamente o
quadrado do erro da etapa anterior.
|