Elon
Lages Lima
IMPA - Estr. D. Castorina
110 - 22460 – Rio de Janeiro – RJ
Continuo a discussão
de pontos controvertidos e conceitos que podem ocasionar dúvidas,
referente a assuntos que são ensinados no primeiro e no segundo grau.
Novamente sugiro que enviem suas perguntas para meu endereço no:
|
Instituto
de Matemática Pura e Aplicada
Edifício Lélio
Gama
Estrada Dona Castorina, 110
CP 22460 – Rio de Janeiro – RJ |
Hoje falaremos
sobre dízimas periódicas, números complexos e o número e. Eis as
indagações que responderemos.
|
Que
significa a igualdade |

Esta é uma das
dez perguntas que apresentei no folheto de lançamento da RPM, visando dar
uma idéia de como seria a seção “Conceitos e Controvérsias” da
nova Revista.
Depois disso,
os leitores Mário Servelli Rosa (de São Paulo, SP), Eliane M. S. Montese
Silva (de Ubá, MG) e Leni Brandão Barletta (de Bragança Paulista, SP)
escreveram pedindo que eu esclarecesse o sentido de igualdades do tipo 1 =
0,999... ou 32,8 = 32,7999...
Há, de fato, motivo para
perplexidade nas fórmulas acima. Examinemos, uma a uma, as igualdades

Na
primeira delas, temos uma fração ordinária irredutível, cujo
denominador não é uma potência de 10, igual a algo que nos parece uma
fração decimal. Na segunda, temos um número inteiro igual a uma fração
decimal (ou algo semelhante). Na terceira, vemos duas frações decimais
de aspectos diferentes mas declaradas iguais. Certamente há razão para dúvidas.
Como ensinar isso a nossos alunos sem antes entendermos bem o que estamos
querendo ensinar?
O
problema todo se situa nas expressões que aparecem nos segundos membros
das igualdades acima: as chamadas “dízimas periódicas”. Se as
interpretarmos corretamente, as dificuldades desaparecerão.
As
dízimas periódicas surgiram como um recurso para socorrer a quem procura
realizar a tarefa impossível de transformar certas frações ordinárias,
como 1/9, 3/11 ou 4/15 em frações decimais.
Uma
fração decimal é, por definição, uma fração (ordinária) cujo
denominador é uma potência de 10. Assim, por exemplo, 3/10, 152/100 e
13/1000 são frações decimais.
Algumas
frações, como 3/5, 7/20 e 6/25, não são, estritamente falando,
decimais (pois seus denominadores não são potências de 10) mas podem
ser escritas como (isto é, são equivalentes a) frações decimais.
Assim, temos:
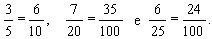
Por outro lado, não existe fração
decimal alguma equivalente à fração irredutível 3/11. Com efeito, as
únicas frações equivalentes a 3/11 são as da forma 3n / 11n, obtidas
multiplicando-se o numerador 3 e o denominador 11 pelo mesmo número
natural n. Ora, qualquer que seja nossa escolha de n, o
denominador 11n jamais será uma potência de 10. O mesmo raciocínio se
aplica às frações 1/9 e 4/15.
Mais geralmente, o argumento acima
prova que um fração irredutível cujo denominador contenha algum fator
primo diferente de 2 ou 5 não é equivalente a uma fração decimal.
(Pois 2 e 5 são os únicos fatores primos que ocorrem numa potência de
10).
Desde a publicação da Aritmética
do holandês Simon Stevin (em 1585), sabe-se da grande vantagem prática
das frações decimais. É fácil escreve-las; é trivial compara-las; é
muito mais fácil realizar com elas as operações aritméticas usuais do
que efetuar as mesmas operações com frações ordinárias
(principalmente somar e subtrair). Pode-se mesmo dizer, sem cometer
exagero, que o uso das frações decimais foi um grande fator de progresso
para a Astronomia, para a Navegação e, conseqüentemente, para a
Humanidade, de um modo geral. Para que tal adoção se desse foi necessário,
entretanto, encontrar um meio de representar qualquer fração sob
forma decimal.
Um momento: não vimos acima
que nenhuma fração decimal é equivalente a 3/11? É verdade. Mas, mesmo
assim, 3/11 pode ser escrita “sob forma decimal”. O segredo está em
admitir frações decimais ilimitadas.
Vejamos
como.
A maneira bem conhecida de
transformar uma fração ordinária como 3/11 em fração decimal consiste
em escrever 3 como 3,0 ou 3,00 ou 3,000 etc. (o número de zeros fica a
nosso critério) e efetuar a divisão por 11. Se tomarmos 4 zeros, por
exemplo, obteremos o quociente 0,2727 e, no lugar do resto, aparece o
algarismo 3. Isto quer dizer que o resto é 0,0003 (já que fomos até décimos
milésimos). Como o dividendo é igual ao divisor vezes o quociente mais o
resto, temos
3,0000 = 11 x 0,2727 +
0,0003.
Dividindo ambos os membros desta
igualdade por 11 e escrevendo 0,0003 sob forma de fração ordinária,
obtemos:
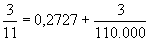
Isto quer dizer que, se
substituirmos a fração ordinária 3/11 pela fração decimal 0,2727,
cometeremos um erro igual a 3/110 000. O mesmo raciocínio mostra que, em
geral, se em lugar de 3/11 escrevemos a fração decimal 0,2727...27 (com
o “período” 27 repetido n vezes) o erro cometido será um fração
cujo numerador é 3 e cujo denominador é 11 x 102n. Este erro
se torna cada vez menor, a medida que n cresce. Tomando n suficientemente
grande, podemos tornar o erro tão pequeno quanto desejemos.
Assim, as frações decimais
(*) 0,27
0,2727 0,272727
etc.
constituem valores aproximados da
fração ordinária 3/11. Quanto maior for o número de algarismos
decimais tomados, menor será o erro cometido (isto é, melhor será a
aproximação). Por isso, quando escrevemos:

não
estamos afirmando que 3/11 = 0,2727. As reticências no fim do símbolo
0,2727... significam que ele não representa uma única fração decimal,
mas a seqüência infinita de frações decimais (*) acima, as quais são
valores aproximados de 3/11.
Agora
podemos entender o que significam as igualdades enunciadas no começo
deste tópico. Na “dízima periódica” 0,111... as reticências são
fundamentais. Elas indicam que 0,111... não é a fração decimal 0,111 e
sim seqüência infinita de frações decimais
0,1
0,11 0,111
0,111 etc.
Cada
uma dessas frações decimais é um valor aproximado par 1/9. Tomando um número
suficientemente grande de algarismos decimais, podemos tornar esta
aproximação tão precisa quanto desejemos. Por exemplo, escrevendo
0,11111 em vez de 1/9 estaremos cometendo um erro igual a
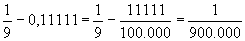 .
.
Explicação
análoga vale para a igualdade 1 = 0,999... A seqüência infinita de frações
decimais
0,9
0,99 0,999
0,9999 etc.
fornece
valores aproximados para o número 1. Por exemplo, a diferença 1 –
0,999999 é igual a 1 milionésimo.
Finalmente,
a igualdade 32,8 = 32,799... significa que a diferença entre 32,8 e
32,799...9 (com n algarismos iguais a 9) pode ser tornada tão
pequena quanto se deseje, desde que se tome um número n
suficientemente grande.
Com
esta discussão, esperamos ter esclarecido o significado da igualdade que
encabeça este tópico, bem como das outras duas, sugeridas pelos colegas
que nos escreveram.
Mas,
para encerrar o assunto, convém lembrar que nem todas as frações
decimais infinitas são periódicas. A periodicidade só aparece quando
procuramos representar uma fração ordinária (número racional) sob
forma decimal. Mas há certos números importantes em Matemática, como
 ,
e, ,
e,
 , etc. que não são racionais, isto é, não podem ser expressos como
quociente de dois números naturais. Eles são chamados números
irracionais. Cada um deles é representado por uma fração decimal
infinita não-periódica.
, etc. que não são racionais, isto é, não podem ser expressos como
quociente de dois números naturais. Eles são chamados números
irracionais. Cada um deles é representado por uma fração decimal
infinita não-periódica.
Vejamos
 ,
por exemplo. Este número é, por definição, a área de um círculo de
raio1 (ou, se preferirem, o comprimento de uma circunferência de raio
1/2) . ,
por exemplo. Este número é, por definição, a área de um círculo de
raio1 (ou, se preferirem, o comprimento de uma circunferência de raio
1/2) .
Inscrevendo
no círculo de raio 1 polígonos regulares cujo número de lados tomamos
cada vez maior, as áreas desses polígonos representam valores
aproximados para a área do círculo, isto é, para o número
 .
Por esse método, ou por outros métodos muito mais sofisticados,
conhecem-se hoje valores aproximados de p
com erros extremamente pequenos. Mais ainda: desde o tempo de Arquimedes
(cerca de 250 anos antes de Cristo) se conhecem algoritmos (isto é,
processos sistemáticos de cálculo) que permitem determinar frações que
aproximam .
Por esse método, ou por outros métodos muito mais sofisticados,
conhecem-se hoje valores aproximados de p
com erros extremamente pequenos. Mais ainda: desde o tempo de Arquimedes
(cerca de 250 anos antes de Cristo) se conhecem algoritmos (isto é,
processos sistemáticos de cálculo) que permitem determinar frações que
aproximam  com a precisão que se deseje. Quando, por exemplo, escrevemos p
= 3,14159265... devemos entender que o segundo membro desta igualdade
representa uma seqüência infinita de frações decimais cujos primeiros
termos são com a precisão que se deseje. Quando, por exemplo, escrevemos p
= 3,14159265... devemos entender que o segundo membro desta igualdade
representa uma seqüência infinita de frações decimais cujos primeiros
termos são
3
3,1 3,14
3,141 3,1415
3,14159 etc.
Cada
fração desta seqüência representa um valor aproximado de
 ,
ou seja, da área do círculo de raio 1. Além disso, os algarismos de
cada fração são exatos, isto é, só se pode obter uma aproximação
melhor, por falta, acrescentando novos algarismos decimais, sem alterar os
que já estão lá. Na seqüência acima não haverá periodicidade, uma
vez que já foi demonstrado (de maneira teórica, com base na Análise
Matemática) que p
não é um número racional. Considerações análogas podem ser feitas
sobre os números e, ,
ou seja, da área do círculo de raio 1. Além disso, os algarismos de
cada fração são exatos, isto é, só se pode obter uma aproximação
melhor, por falta, acrescentando novos algarismos decimais, sem alterar os
que já estão lá. Na seqüência acima não haverá periodicidade, uma
vez que já foi demonstrado (de maneira teórica, com base na Análise
Matemática) que p
não é um número racional. Considerações análogas podem ser feitas
sobre os números e,
 , etc.
, etc.
|
Qual destes números
é o maior?
|
Resposta:
nenhum dos dois, porque o corpo ¢ dos números complexos não é
ordenado.
Lembremos
que um conjunto X diz-se ordenado quando está definida entre seus
elementos uma relação de ordem, ou seja, uma relação binária x
< y, com as seguintes propriedades:
1)
Dados arbitrariamente x e y em X, ou se tem x
< y, ou y < x, ou x = y, cada uma dessas possibilidades excluindo as demais (tricotomia).
2)
Se x < y e y < z então x <
z (transitividade).
Posta
esta definição, cabe a pergunta: o que impede alguém de ordenar o
conjunto ¢ dos números complexos? Por exemplo, o que estará errado se
tomarmos em ¢ a “ordem do dicionário”? Esta ordem é a seguinte:
dados os números complexos w = a + bi e z = c + di
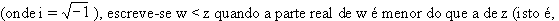 quando a < c) e, naturalmente, põe-se z < w se c < a.
Quando, porém, se tem a = c, apela-se para a parte imaginária, ou seja,
diz-se que w < z quando b < d e z < w no caso de d < b. As
propriedades 01 e 02 são facilmente verificadas para a ordem do dicionário,
logo ela torna o conjunto ¢ dos números complexos um conjunto ordenado.
E agora?
quando a < c) e, naturalmente, põe-se z < w se c < a.
Quando, porém, se tem a = c, apela-se para a parte imaginária, ou seja,
diz-se que w < z quando b < d e z < w no caso de d < b. As
propriedades 01 e 02 são facilmente verificadas para a ordem do dicionário,
logo ela torna o conjunto ¢ dos números complexos um conjunto ordenado.
E agora?
Não
há contradição. Qualquer conjunto pode ser ordenado (de muitas
maneiras). Mas a resposta acima diz que ¢ não é um corpo
ordenado.
Entre
os números complexos estão definidas duas operações, adição e
multiplicação, as quais são comutativas, associativas e a multiplicação
é distributiva relativamente à adição. Além disso, todo número
complexo z possui um inverso aditivo –z, caracterizado pela igualdade
–z + z = 0. E todo complexo z ¹
0 tem um inverso multiplicativos z -1, tal que zz -1 =
1. Por causa dessas propriedades diz-se que o conjunto ¢ dos números
complexos é um corpo.
O
conjunto dos números racionais e o conjunto R dos números reais
também são corpos em relação às operações de adição e multiplicação
usuais.
Um
corpo ordenado é um corpo no qual se definiu uma relação de
ordem “compatível” com as operações de adição e de multiplicação,
ou seja, com as seguintes propriedades:
CO1)
Se x < y então x + z < y + z para todo z no corpo;
CO2)
Se x < y então xz < yz para todo z > 0 no corpo.
Por
exemplo, a definição “x < y quando y – x é um número
positivo” faz do corpo R dos números reais um corpo ordenado (o
mesmo ocorrendo com o corpo Q dos racionais).
Por
outro lado, a ordem do dicionário, que definimos acima no conjunto ¢ dos
números complexos, não faz de ¢ um corpo ordenado. Com efeito, ela
cumpre a condição CO1), ou seja, é compatível com a adição de números
complexos, mas não cumpre a condição CO2). Para comprovar esta afirmação,
observemos primeiro que, na ordem do dicionário, os números complexos
maiores do que zero são os que ou têm parte real positiva ou são da
forma z = 0 + bi = bi com b > 0. Em seguida, notemos que vale 2 + 3i
< 3 + 2i na ordem do dicionário mas, multiplicando ambos os membros
desta desigualdade pelo número complexo “positivo” 2 – 3i obtemos
13 < 12 – 5i, uma desigualdade falsa na ordem do dicionário.
A
resposta que demos no início significa que NENHUMA relação de ordem
entre os números complexos pode tornar ¢ um corpo ordenado. Como se
prova isto? De modo simples, como conseqüência dos seguintes argumentos:
a)
Num corpo
ordenado, tem-se x > 0 se, e somente se, – x < 0.
Com
efeito, supondo x > 0 e somando –x a ambos os membros, obtém-se 0
> – x, ou seja, –x < 0. Reciprocamente, se –x
< 0, somando x a ambos os membros vem 0 < x, ou seja, x >
0.
b)
Num corpo ordenado, o quadrado de todo elemento não nulo é
positivo, isto é, x  0 implica x2 > 0.
0 implica x2 > 0.
Com
efeito, sendo x  0, deve-se te x > 0 ou x < 0. No primeiro caso, multiplicando ambos
os membros da desigualdade x > 0 pelo elemento positivo x, obtemos x2
> 0. No segundo caso, segue-se de a) que –x > 0. Pelo primeiro
caso, tem-se (-x)2 > 0. Mas (-x)2 = x2,
logo x2 > 0 em qualquer caso.
0, deve-se te x > 0 ou x < 0. No primeiro caso, multiplicando ambos
os membros da desigualdade x > 0 pelo elemento positivo x, obtemos x2
> 0. No segundo caso, segue-se de a) que –x > 0. Pelo primeiro
caso, tem-se (-x)2 > 0. Mas (-x)2 = x2,
logo x2 > 0 em qualquer caso.
c)
Em todo corpo ordenado, 1 é positivo, logo –1 é negativo.
Com
efeito, 1 é o quadrado de 1, logo 1 > 0 (por b) e daí –1 < 0
(por a)).
d)
Nenhuma relação de ordem torna o corpo ¢
dos números complexos um corpo ordenado.
Com
efeito, temos –1 = i2. Se ¢ fosse um corpo ordenado,
o número –1 seria negativo em virtude de c) e positivo em virtude de
b), uma contradição.
A
noção de logaritmo quase sempre nos é apresentada, pela primeira vez,
do seguinte modo: “o logaritmo de um número y na base a é o
expoente x tal que ax = y”. Segue-se a observação:
“os números mais freqüentemente usados como base de um sistema de
logaritmos são 10, que é a base do nosso sistema de numeração, e o número
e = 2,71828182...” Isto nos deixa intrigados.
De
saída, uma pergunta ingênua: esta regularidade na seqüência dos
algarismos decimais deste número persiste? Não. Apenas uma coincidência
no começo. Um valor mais preciso seria
e = 2,718281828459...
Não
se trata de uma fração decimal periódica. O número e é
irracional, isto é, não pode ser obtido como quociente e = p/q de dois
inteiros. Mais ainda: é um irracional transcendente. Isto
significa que não existe um polinômio P (x) com coeficiente inteiros,
que se anule para x = e.
Por
que então a escolha de um número tão estranho como base de logaritmos?
Mesmo
depois de aprender que

a indagação ainda persiste: o que faz esse número tão importante?
Isto é o que procurarei responder aqui.
Talvez
a resposta mais concisa seja que o número “e” é importante porque é
inevitável. Surge espontaneamente em várias questões básicas.
Uma
das razões pelas quais a Matemática é útil às Ciências em geral está
no Cálculo (Diferencial e Integral), que estuda a variação das
grandezas. E um tipo de variação dos mais simples e comumente
encontrados é aquele em que o crescimento (ou decrescimento) da grandeza
em cada instante é proporcional ao valor da grandeza naquele instante.
Este tipo de variação ocorre, por exemplo, em questões de juros,
crescimento populacional (de pessoas ou bactérias), desintegração
radioativa, etc. Em todos os fenômenos desta natureza, o número e aparece
de modo natural e insubstituível. Vejamos um exemplo simples.
Suponhamos
que eu empreste a alguém a quantia de 1 cruzeiro a juros de 100% ao ano.
No final do ano, essa pessoa viria pagar-me e traria 2 cruzeiros: 1 que
tomara emprestado e 1 dos juros. Isto seria justo? Não. O justo seria que
eu recebesse e cruzeiros. Vejamos por que. Há um entendimento tácito
nessas transações de que os juros são proporcionais ao capital
emprestado e ao tempo decorrido entre o empréstimo e o pagamento. Assim,
se meu cliente  dinheiro mais seis meses, à taxa de 100% ao ano, logo deveria
pagar-me dinheiro mais seis meses, à taxa de 100% ao ano, logo deveria
pagar-me

cruzeiros
no fim do ano. Isto me daria 2,25 cruzeiros mas, mesmo assim, eu não
acharia justo. Eu poderia dividir o ano num número arbitrário n
de partes iguais. Transcorrido o primeiro
 n,
segue-se que o justo e exato valor que eu deveria receber pelo meu
cruzeiro emprestado
n,
segue-se que o justo e exato valor que eu deveria receber pelo meu
cruzeiro emprestado 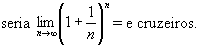
Mais
geralmente, se eu empresto c cruzeiros a juros de k% ao ano,
transcorridos t anos eu devo receber de volta c.eat
cruzeiros, onde a
= k/100. Para maiores detalhes e outros exemplos, relativos a
desintegração radioativa, crescimento populacional, etc., veja o
livrinho “Logaritmos”, de minha autoria, publicado pela S.B.M.
Os
logaritmos que tem base e são às vezes impropriamente chamados de
“logaritmos neperianos”. Na realidade, os logaritmos originalmente
introduzidos por Napier tinham por base o número a = (1 – 10-7)7.
Aliás, para sermos mais exatos, o verdadeiro “logaritmo neperiano” do número x era igual a
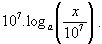
É mais apropriado chamar logaritmos naturais
aos logaritmos de
base e. Euler os chamava de logaritmos hiperbólicos, pelo seguinte
motivo. Consideremos a função f: R+
 R, definida por f(x) = 1/x. Seu gráfico é um ramo de hipérbole
eqüilátera. Para cada número real a > 0, seja
R, definida por f(x) = 1/x. Seu gráfico é um ramo de hipérbole
eqüilátera. Para cada número real a > 0, seja
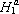 a faixa de hipérbole formada
pelos pontos de plano cujas coordenadas (x, y) satisfazem às
desigualdades 0
a faixa de hipérbole formada
pelos pontos de plano cujas coordenadas (x, y) satisfazem às
desigualdades 0  y y
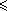 1/x e 1
1/x e 1 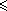 x x
 a (se a a (se a
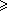 1) ou a
1) ou a  x x
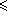 1 (se a
1 (se a  1). 1).

A
área de
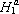 é igual ao logaritmo natural
de a se for a
é igual ao logaritmo natural
de a se for a 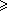 1 e a esse logaritmo com sinal trocado se for a
1 e a esse logaritmo com sinal trocado se for a
 1. Em particular, o número e é a abscissa tal que
1. Em particular, o número e é a abscissa tal que
 tem área igual a 1. O fato de que a área da faixa de hipérbole
tem área igual a 1. O fato de que a área da faixa de hipérbole
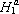 é igual ao logaritmo natural
de a pode ser tomado como definição de logaritmo e permite desenvolver a
teoria, a partir daí, de modo simples e elegante. Esta abordagem é
adotada em nosso livro acima citado.
é igual ao logaritmo natural
de a pode ser tomado como definição de logaritmo e permite desenvolver a
teoria, a partir daí, de modo simples e elegante. Esta abordagem é
adotada em nosso livro acima citado.
“O
logaritmo hiperbólico pode ser caracterizado pela igualdade log (1 + x) =
x, para todo número infinitamente pequeno x.” Esta frase é de Euler.
Evidentemente, na teoria habitual dos números reais, não há números
infinitamente pequenos. O que Euler quis dizer é que log(1 + x) e x são
“infinitésimos equivalentes” ou, de modo mais preciso, que

Esta
igualdade só é verdadeira quando a base do sistema de logaritmos é o número
e. Se tomarmos logaritmos numa base a teremos
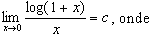
onde c é o logaritmo natural de a. Na verdade, esta fórmula é um caso
particular do fato de que a derivada da função log x é igual a c/x.
Aqui tomamos log x numa base a qualquer. Se a base for e então
a derivada de log x será 1/x. (No caso geral c = logea).
Mais uma vez, vemos que a base e é mais “natural”.
|
O
máximo em paranóia
|
|
O
eminente matemático inglês G. H. Hardy (1877-1947) tinha algumas
idéias fixas. Uma delas era a de demonstrar a chamada “hipótese
de Riemann” (um famoso problema sobre variáveis complexas, até
hoje não resolvido). A outra era de que Deus era seu inimigo
pessoal e o perseguia incessantemente. Certa feita, ao regressar
de uma viagem à Dinamarca, num barco pequeno e mar bravio, enviou
de bordo um telegrama a seu amigo,
o matemático Harald Bohr, em Coponhague, contendo a
mensagem: “Consegui provar a hipótese de Riemann”. Seu raciocínio
era o seguinte: se o navio naufragasse (coisa que ele muito
temia), ele passaria à História como tendo resolvido um dificílimo
problema matemático, todos supondo que sua demonstração
afundara com ele. Como, entretanto, Deus o odiava, não ia
permitir que isso acontecesse; protegeria a viagem e ele chegaria
são e salvo à Inglaterra.
|
|