Prova de Matemática do Concurso do
Magistério Estadual do Rio de Janeiro
(16/12/90)
 

      Questões de números 31 a 51. (Gabarito: p.  14.)

31. Numa régua graduada, o segmento cujos extremos são X = 7, 13 e Y = 8,32 se encontra dividido em sete partes iguais, conforme se vê na figura abaixo. 0 número decimal Z, correspondente à terceira divisão a partir da extremidade X,   é expresso por:

A)   7,30                        
 B)   7,45                              
C)   7,60                          
D)   7,64                                   
E)    7,82

32. O número natural   N = 82 x 55p  possui 700 divisores positivos.  O valor de p  é:

A)   5                      B)   6                      C)   7                      D)   8                      E)   9

33. Considere a definição: Uma função f : A B é sobrejetora .se e só se y B , x A , f(x) = y. Sua negação se expressa por: f : A B é não sobrejetora se e só se ocorrer:

A)  correio

B)   errado, pois o correio é   l x < 2

C)   errado, pois foi admitido que   x 2 0

D)   errado, pois foi admitido unicamente que   x 2 > 0

E)   errado, pois não foi trocado o sentido da desigualdade



A)   1                      B)   2/3       C)   1/3          D)  2/9             E)   1/9

 

A)   tg x          B)  cos x          C)  sec x           D)   cotg x          E)   cosec x
 

37. As soluções da equação   3x+1 + 34 - x 36 = 0   são   a e b, sendo   a < b.    O valor de   log3 (a + b) + log3 (b a)  é:

A)   1                    B)  2                     C)  3                        D)  4                          E)  5


38. Se a equação   2x2 + px + q = 0,   com   p e q reais, admite a raiz complexa 3 2i,   então  q  é igual a:

A)   -13               B)   5              C)   6                D)  13                 E)  26


39. O valor do parâmetro   m,   para que o sistema

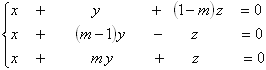
admita soluções distintas de   (0,0,0),  é:
A)  - 2                   B)  - 1                   C)  - 1/2                  D)   1                   E)  2


40. Para fabricar placas de automóvel, constituídas de duas letras iniciais seguidas de quatro algarismos, um determinado município está autorizado a utilizar somente as letras A, B, C, D e E e os algarismos 0, 1 e 2. Nessas condições, o número máximo de automóveis que o município poderá emplacar é:

A)   120              B)   1620              C)  2025               D)  2048               E)  2592


41. A tabela seguinte fornece, por sexo e por curso, o número de estudantes matriculados num colégio estadual

 

Escolhendo, ao acaso, um desses estudantes e representando por p1 a probabilidade de o elemento escolhido ser homem ou ser do Curso de Formação Geral e por p2, a probabilidade de o elemento escolhido ser mulher, dado que é do Curso de Formação de Professores, pode-se concluir que:

42.  Se   ABCDA'B'C'D'  é um cubo de aresta a, então a pirâmide de vértice  D' e base   ABCD   tem área lateral igual a:

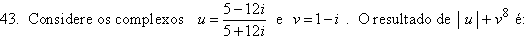
A)   13                  B)   15                  C)   17                  D)   19                  E)  21

44. Considere o triângulo ABC inscrito em um círculo de raio r. Os lados AB e AC medem, respectivamente, 10 cm e 8 cm e a altura relativa ao vértice A mede 5 cm. A medida, em cm, do raio  r  é:


45. Considere as matrizes:

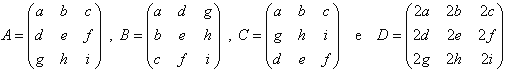
Se o determinante da matriz A é k(k b 0), então det (B) + det (C) + det (D) é igual:

A)  10 k               B)  8 k                  C)  6 k                  D)  4 k                  E)  2 k

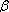46.  Considere a figura abaixo.  Sabendo que   FC = FE,   pode-se afirmar que o valor de      em função de     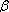 e   , ( < ), é:

47. O número de soluções da equação  2 tg2 x + 3 sec x = 0,   no intervalo   [0, 2], é:

A)   0          B)   1          C)   2          D)  3          E)  4


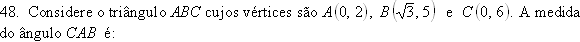
A)   30°               B)   45°               C)   60°               D)   90°               E)   120°


49.  Para obter o resultado da expressão

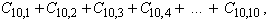
sendo Cm,p o número de combinações simples de m elementos tomados p a p, um professor, evitando o cálculo de cada uma destas parcelas, aplica o desenvolvimento do Binômio de Newton para concluir que esta soma vale:

A)  210               B)   210+1               C)  210 + 1             D)  210-1                 E)  210 - 1


50.  Considere os conjuntos:

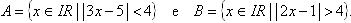
A intersecção entre   A e B   corresponde ao seguinte intervalo:

51. Uma função f é definida em A e tem imagem em B. O conjunto A tem m elementos e o conjunto B tem  p elementos. Sabendo-se que a função f é sobrejetora, pode-se afirmar que:

A) p = m               B) p m               C) p < m               D) p > m               E) p m